Published online by Cambridge University Press: 12 March 2014
We study the expressive power in the finite of the logic Fixed-Point+Counting, the extension of first-order logic which is obtained through adding both the fixed-point constructor and the ability to count.
To this end an isomorphism preserving (‘generic’) model of computation is introduced whose PTime restriction exactly corresponds to this level of expressive power, while its PSpace restriction corresponds to While+Counting. From this model we obtain a normal form which shows a rather clear separation of the relational vs. the arithmetical side of the algorithms involved.
In parallel, we study the relations of Fixed-Point+Counting with the infinitary logics 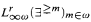 and the corresponding pebble games.
and the corresponding pebble games.
The main result, however, involves the concept of an arithmetical invariant. By this we mean a functor taking every finite relational structure to an expansion of (an initial segment of) the standard arithmetical structure. In particular its values are linearly ordered structures. We establish the existence of a family of arithmetical invariants 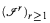 with the following properties:
with the following properties:
• The invariants themselves can be evaluated in polynomial time.
• A class of finite relational structures is definable in Fixed-Point+Counting if and only if membership can be decided in polynomial time on the basis of the values of one of the invariants.
• The invariant 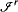 r classifies all finite relational structures exactly up to equivalence with respect to the logic
r classifies all finite relational structures exactly up to equivalence with respect to the logic 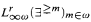
We also give a characterization of Fixed-Point+Counting in terms of sequences of formulae in the 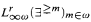 : It corresponds exactly to the polynomial time computable families (φn)n ∈ ω in these logics.
: It corresponds exactly to the polynomial time computable families (φn)n ∈ ω in these logics.
Towards a positive assessment of the expressive power of Fixed-Point+Counting, it is shown that the natural extension of fixed-point logic by Lindström quantifiers, which capture all the PTime computable properties of cardinalities of definable predicates, is strictly weaker than what we get here. This implies in particular that every extension of fixed-point logic by means of monadic Lindström quantifiers, which stays within PTime, must be strictly contained in Fixed-Point+Counting.