Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-25T00:37:19.875Z Has data issue: false hasContentIssue false
  • English
  • Français

Explicit mathematics with the monotone fixed point principle. II: Models

Published online by Cambridge University Press:  12 March 2014

Michael Rathjen
Michael Rathjen*
Affiliation:
Department of Pure Mathematics, University of Leeds, Leeds LS2 9JT, England E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper continues investigations of the monotone fixed point principle in the context of Feferman's explicit mathematics begun in [14]. Explicit mathematics is a versatile formal framework for representing Bishop-style constructive mathematics and generalized recursion theory. The object of investigation here is the theory of explicit mathematics augmented by the monotone fixed point principle, which asserts that any monotone operation on classifications (Feferman's notion of set) possesses a least fixed point. To be more precise, the new axiom not merely postulates the existence of a least solution, but, by adjoining a new constant to the language, it is ensured that a fixed point is uniformly presentable as a function of the monotone operation. Let T0 + UMID denote this extension of explicit mathematics. [14] gave lower bounds for the strength of two subtheories of To + UMID in relating them to fragments of second order arithmetic based on 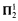comprehension. [14] showed that To ↾ + UMID and To ↾ + INDk + UMID have at least the strength of ( 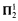– CA), and ↾ and 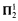– CA), respectively.

Here we are concerned with the exact reversals. Let UMIDN be the monotone fixed-point principle for subclassifications of the natural numbers. Among other results, it is shown that To ↾ + UMIDN and To ↾ + INDN + UMIDN have the same strength as (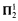 – CA) ↾ and ( 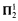– CA), respectively.

The results are achieved by constructing set-theoretic models for the aforementioned systems of explicit mathematics in certain extensions of Kripke-Platek set theory and subsequently relating these set theories to subsystems of second arithmetic.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 64 , Issue 2 , June 1999 , pp. 517 - 550
Copyright
Copyright © Association for Symbolic Logic 1999

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Aczel, P., The type theoretic interpretation of constructive set theory: Inductive definitions, (Marcus, R. B. et al., editor), Logic, Methodology, and Philosophy of Science VII, North-Holland, Amsterdam, 1986.Google Scholar
[2] Apt, K.R. and Marek, W., Second order arithmetic and related topics, Annals of Mathematical Logic, vol. 6 (1974), pp. 117–229.CrossRefGoogle Scholar
[3] Barwise, J., Admissible sets and structures, Springer, Berlin, 1975.CrossRefGoogle Scholar
[4] Barwise, J. and Fischer, E., The Shoenfield absoluteness lemma, Israel Journal of Mathematics, vol. 8 (1970), pp. 329–339.CrossRefGoogle Scholar
[5] Devlin, K., Constructibility, Springer, Berlin, 1984.CrossRefGoogle Scholar
[6] Feferman, S., A language and axioms for explicit mathematics, Algebra and logic (Crossley, J.N., editor), Lecture Notes in Mathematics, vol. 450, Springer, Berlin, 1975, pp. 87–139.CrossRefGoogle Scholar
[7] Feferman, S., Recursion theory and set theory: a marriage of convenience. Generalized recursion theory II (Sacks, G.E. Fenstad, J.E., Gandy, R.O., editor), North-Holland, Amsterdam, 1978, pp. 55–98.Google Scholar
[8] Feferman, S., Constructive theories of functions and classes, Logic colloquium ’78 (Boffa, M., van Dalen, D., and McAloon, K., editors), North-Holland, Amsterdam, 1979, pp. 159–224.Google Scholar
[9] Feferman, S., Monotone inductive definitions, The L.E.J. Brouwer centenary symposium (Troelstra, A. S. and van Dalen, D., editors), North-Holland, Amsterdam, 1982, pp. 77–89.Google Scholar
[10] Giaß, T., Rathjen, M., and Schlüter, A., On the proof-theoretic strength of monotone induction in explicit mathematics, Annals of Pure and Applied Logic, vol. 85 (1997), pp. 1–46.Google Scholar
[11] Hinman, P.G., Recursion-theoretic hierarchies, Springer, Berlin, 1978.CrossRefGoogle Scholar
[12] Jäger, G., Theories for admissible sets: a unifying approach to proof theory, Bibliopolis, Naples, 1986.Google Scholar
[13] Rathjen, M., Monotone inductive definitions in explicit mathematics, this Journal, vol. 61 (1996), pp. 125–146.Google Scholar
[14] Rathjen, M., Explicit mathematics with the monotone fixed point principle, this Journal, vol. 63 (1998), pp. 509–542.Google Scholar
[15] Simpson, S.G., Set theoretic aspects of ATR0 , Logic colloquium ’80 (van Dalen, D., Lascar, D., and Smiley, J., editors), North-Holland, Amsterdam, 1982, pp. 255–271.Google Scholar
[16] Takahashi, S., Monotone inductive definitions in a constructive theory of functions and classes, Annals of Pure and Applied Logic, vol. 42 (1989), pp. 255–279.CrossRefGoogle Scholar