Hostname: page-component-6bf8c574d5-9nwgx Total loading time: 0 Render date: 2025-02-26T13:54:49.551Z Has data issue: false hasContentIssue false
  • English
  • Français

Expansions of models and turing degrees

Published online by Cambridge University Press:  12 March 2014

Julia Knight  and
Mark Nadel
Julia Knight
Affiliation:
University of Notre Dame, Notre Dame, Indiana 46556
Mark Nadel
Affiliation:
University of Notre Dame, Notre Dame, Indiana 46556
Get access Rights & Permissions [Opens in a new window]

Extract

If 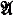is a countable recursively saturated structure and T is a recursively axiomatizable theory that is consistent with Th(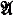), then it is well known that 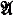can be expanded to a recursively saturated model of T [7, p. 186]. This is what has made recursively saturated models useful in model theory. Recursive saturation is the weakest notion of saturation for which this expandability result holds. In fact, if 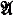is a countable model of Pr = Th(ω, +), then 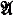can be expanded to a model of first order Peano arithmetic P just in case 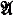is recursively saturated (see [3]).

In this paper we investigate two natural sets of Turing degrees that tell a good deal about the expandability of a given structure. If 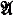is a recursively saturated structure, I(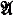) consists of the degrees of sets that are recursive in complete types realized in 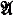. The second set of degrees, D(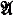), consists of the degrees of sets S such that 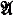is recursive in S-saturated. In general, I(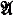) ⊆ D(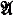). Moreover, I(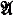) is obviously an “ideal” of degrees. For countable structures 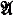, D(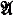) is “closed” in the following sense: For any class C ⊆ 2ω, if C is co-r.e. in S for some set S such that 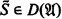, then there is some σ ∈ C such that . For uncountable structures 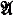, we do not know whether D(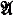) must be closed.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 47 , Issue 3 , September 1982 , pp. 587 - 604
Copyright
Copyright © Association for Symbolic Logic 1982

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Jockusch, C. G. Jr. and Soare, R. I., Π10-classes and degrees of theories, Transactions of the American Mathematical Society, vol. 173 (1972), pp. 33–56.Google Scholar
[2]Kunen, K., Combinatorics, Handbook of Mathematical Logic (Barwise, J., editor), North-Holland, Amsterdam, 1977, pp. 371–401.CrossRefGoogle Scholar
[3]Lipshitz, L. and Nadel, M., The additive structure of models of arithmetic, Proceedings of the American Mathematical Society, vol. 68 (1978), pp. 331–336.CrossRefGoogle Scholar
[4]MacDowell, R. and Specker, E., Modelle der Arithmetik, Infinitistic methods, Pergamon, London, 1961, pp. 257–263.Google Scholar
[5]Nadel, M., On a problem of MacDowell and Specker, this Journal, vol. 45 (1980), pp. 612–622.Google Scholar
[6]Rogers, H., Theory of recursive functions and effective computability, McGraw-Hill, New York, 1967.Google Scholar
[7]Schlipf, J. S., Model theory and recursive saturation, this Journal, vol. 43 (1978), pp. 183–206.Google Scholar
[8]Scott, D., Algebras of sets binumerable in complete extensions of arithmetic, Recursive function theory, Proceedings of Symposia in Pure Mathematics, vol. 5, American Mathematical Society, Providence, R.I., 1962, pp. 117–121.CrossRefGoogle Scholar
[9]Simpson, S., Degrees of unsolvability, Handbook of Mathematical Logic (Barwise, J., editor), North-Holland, Amsterdam, 1977, pp. 631–665.CrossRefGoogle Scholar
[10]Simpson, S., Sets which do not have subsets of every higher degree, this Journal, vol. 43 (1978), pp. 135–138.Google Scholar
[11]Szmielew, W., Elementary properties of Abelian groups, Fundamenta Mathematicae, vol. 41 (1954), pp. 203–271.CrossRefGoogle Scholar