Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-25T07:20:04.876Z Has data issue: false hasContentIssue false
  • English
  • Français

Equivalence structures and isomorphisms in the difference hierarchy

Published online by Cambridge University Press:  12 March 2014

Douglas Cenzer ,
Geoffrey Laforte  and
Jeffrey Remmel
Douglas Cenzer
Affiliation:
Department of Mathematics, University of Florida, Gainesville, FL 32611-8105, USA, E-mail: [email protected]
Geoffrey Laforte
Affiliation:
Department of Mathematics and Statistics, University of West Florida, Pensacola, Fl 32514, USA, E-mail: [email protected]
Jeffrey Remmel
Affiliation:
Department of Mathematics, University of California at San Diego, La Jolla, Ca 92093-0112, USA, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We examine the effective categoricity of equivalence structures via Ershov's difference hierarchy. We explore various kinds of categoricity available by distinguishing three different notions of isomorphism available in this hierarchy. We prove several results relating our notions of categoricity to computable equivalence relations: for example, we show that, for such relations, computable categoricity is equivalent to our notion of weak ω-c.e. categoricity, and that 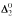-categoricity is equivalent to our notion of graph-ω-c.e. categoricity.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 74 , Issue 2 , June 2009 , pp. 535 - 556
Copyright
Copyright © Association for Symbolic Logic 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Calvert, W., Cenzer, D., Harizanov, V., and Morozov, A., Effective categoricity of equivalence structures, Annals of Pure and Applied Logic, vol. 141 (2006), pp. 61–78.CrossRefGoogle Scholar
[2]Khisamiev, N. G., Constructive abelian p-groups, Siberian Advances in Mathematics, vol. 2 (1992), pp. 68–113.Google Scholar
[3]Khoussainov, B., Stephan, F., and Yang, Y., Computable categoricity and the Ershov hierarchy, unpublished.Google Scholar
[4]Soare, R. I., Recursively enumerable sets and degrees, Springer-Verlag, Berlin, 1987.CrossRefGoogle Scholar