Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-22T20:21:11.141Z Has data issue: false hasContentIssue false
  • English
  • Français

EQUIVALENCE RELATIONS WHICH ARE BOREL SOMEWHERE

Published online by Cambridge University Press:  08 September 2017

WILLIAM CHAN
WILLIAM CHAN*
Affiliation:
DEPARTMENT OF MATHEMATICS CALIFORNIA INSTITUTE OF TECHNOLOGY PASADENA, CA91106, USA E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The following will be shown: Let I be a σ-ideal on a Polish space X so that the associated forcing of I+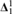${\bf{\Delta }}_1^1$ sets ordered by ⊆ is a proper forcing. Let E be a 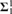${\bf{\Sigma }}_1^1$ or a 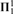${\bf{\Pi }}_1^1$ equivalence relation on X with all equivalence classes 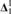${\bf{\Delta }}_1^1$. If for all 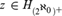$z \in {H_{{{\left( {{2^{{\aleph _0}}}} \right)}^ + }}}$, z♯ exists, then there exists an I+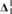${\bf{\Delta }}_1^1$ set C ⊆ X such that E ↾ C is a 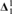${\bf{\Delta }}_1^1$ equivalence relation.

Keywords

03E1503E3503E55equivalence relationsproper forcingsidealsdescriptive set theoryBorel setsanalytic sets
Type
Articles
Information
The Journal of Symbolic Logic , Volume 82 , Issue 3 , September 2017 , pp. 893 - 930
Copyright
Copyright © The Association for Symbolic Logic 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Apter, A. W., Gitman, V., and Hamkins, J. D., Inner models with large cardinal features usually obtained by forcing . Archive for Mathematical Logic, vol. 51 (2012), no. 3–4, pp. 257–283.Google Scholar
Bagaria, J. and Friedman, S. D., Generic absoluteness . Proceedings of the XIth Latin American Symposium on Mathematical Logic (Mérida, 1998), vol. 108 (2001), pp. 3–13.Google Scholar
Burgess, J. P., Descriptive set theory and infinitary languages , Set Theory, Foundations of Mathematics (Proceeding of Symposia, Belgrade, 1977), Matematički institut SANU (Nova Serija), Zbornik Radova, vol.2(10), 1977, pp. 9–30.Google Scholar
Burgess, J. P., Effective enumeration of classes in a ${\rm{\Sigma }}_1^1$ equivalence relation . Indiana University Mathematics Journal, vol. 28 (1979), no. 3, pp. 353–364.Google Scholar
Caicedo, A. E. and Schindler, R., Projective well-orderings of the reals . Archive for Mathematical Logic, vol. 45 (2006), no. 7, pp. 783–793.Google Scholar
Chan, W., The countable admissible ordinal equivalence relation. Annals of Pure and Applied Logic, vol. 168 (2016), pp. 1224–1246.CrossRefGoogle Scholar
Chan, W., Canonicalization by absoluteness, Notes.Google Scholar
Chan, W. and Magidor, M., When an equivalence relation with all Borel classes will be Borel somewhere? 2016, arXiv e-prints.Google Scholar
Clemens, J. D., Equivalence relations which reduce all Borel equivalance relations, Available at http://www.math.uni-muenster.de/u/jclemens/public/Papers/aboveBorel.pdf.Google Scholar
Devlin, K. J., An introduction to the fine structure of the constructible hierarchy (results of Ronald Jensen (Ann. Math. Logic 4 (1972), 229–308; erratum, ibid. 4(1972), 443)) , Generalized Recursion Theory (Proceedings of Symposia, University of Oslo, Oslo, 1972), Studies in Logic and the Foundations of Mathematics, vol. 79, North-Holland, Amsterdam, 1974, pp. 123–163.Google Scholar
Drucker, O., Borel canonization of analytic sets with Borel sections, 2015, arXiv e-prints.Google Scholar
Feng, Q., Magidor, M., and Woodin, H., Universally Baire sets of reals , Set Theory of the Continuum (Berkeley, CA, 1989), Mathematical Sciences Research Institute Publications, vol. 26, Springer, New York, 1992, pp. 203–242.Google Scholar
Friedman, S. D., Minimal coding . Annals of Pure and Applied Logic, vol. 41 (1989), no. 3, pp. 233–297.CrossRefGoogle Scholar
Hamkins, J. D. and Hugh Woodin, W., The necessary maximality principle for c.c.c. forcing is equiconsistent with a weakly compact cardinal . Mathematical Logic Quarterly, vol. 51 (2005), no. 5, pp. 493–498.Google Scholar
Hjorth, G., Thin equivalence relations and effective decompositions, this Journal, vol. 58 (1993), no. 4, pp. 1153–1164.Google Scholar
Jech, T., Set Theory, Springer Monographs in Mathematics, Springer-Verlag, Berlin, 2003.Google Scholar
Jensen, R. B., The fine structure of the constructible hierarchy . Annals of Mathematical Logic, vol. 4 (1972), pp. 229–308; erratum, ibid. 4(1972), 443.CrossRefGoogle Scholar
Jensen, R., Definable sets of minimal degree . Studies in Logic and the Foundations of Mathematics, vol. 59 (1970), pp. 122–128.Google Scholar
Kanovei, V., Sabok, M., and Zapletal, J., Canonical Ramsey Theory on Polish Spaces, Cambridge Tracts in Mathematics, vol. 202, Cambridge University Press, Cambridge, 2013.CrossRefGoogle Scholar
Kechris, A. S., Measure and category in effective descriptive set theory . Annals of Mathematical Logic, vol. 5 (1972/73), pp. 337–384.Google Scholar
Kechris, A. S., Classical Descriptive Set Theory, Graduate Texts in Mathematics, vol. 156, Springer-Verlag, New York, 1995.Google Scholar
Kechris, A. S. and Louveau, A., The classification of hypersmooth Borel equivalence relations . Journal of the American Mathematical Society, vol. 10 (1997), no. 1, pp. 215–242.Google Scholar
Kunen, K., Set Theory, Studies in Logic (London), vol. 34, College Publications, London, 2011.Google Scholar
Mansfield, R. and Weitkamp, G., Recursive Aspects of Descriptive Set Theory, Oxford Logic Guides, vol. 11, The Clarendon Press, Oxford University Press, New York, 1985.Google Scholar
Martin, D. A. and Solovay, R. M., A basis theorem for ${\rm{\Sigma }}_3^1$ sets of reals . Annals of Mathematics (2), vol. 89 (1969), pp. 138–159.Google Scholar
Martin, D. A. and Solovay, R. M., Internal Cohen extensions . Annals of Mathematical Logic, vol. 2 (1970), no. 2, pp. 143–178.Google Scholar
Neeman, I. and Norwood, Z., Happy and mad families in L(ℝ), Available at http://www.math.ucla.edu/∼ineeman.Google Scholar
Schindler, R., Set Theory, Universitext, Springer, Cham, 2014.Google Scholar
Schindler, R. and Zeman, M., Fine structure , Handbook of Set Theory (Foreman, M. and Kanamori, A., editors), Springer, Dordrecht, 2010, pp. 605–656.Google Scholar
Schindler, R.-D., Proper forcing and remarkable cardinals. II, this Journal, vol. 66 (2001), no. 3, pp. 1481–1492.Google Scholar
Shelah, S., Can you take Solovay’s inaccessible away? Israel Journal of Mathematics, vol. 48 (1984), no. 1, pp. 1–47.Google Scholar
Solovay, R. M., A model of set-theory in which every set of reals is Lebesgue measurable . Annals of Mathematics (2), vol. 92 (1970), pp. 1–56.Google Scholar
Zapletal, J., Descriptive set theory and definable forcing . Memoirs of the American Mathematical Society, vol. 167 (2004), no. 793.Google Scholar
Zapletal, J., Forcing Idealized, Cambridge Tracts in Mathematics, vol. 174, Cambridge University Press, Cambridge, 2008.Google Scholar