Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Martin, Donald A.
1990.
An extension of borel determinacy.
Annals of Pure and Applied Logic,
Vol. 49,
Issue. 3,
p.
279.
DuBose, Derrick Albert
1991.
Determinacy and the sharp function on the reals.
Annals of Pure and Applied Logic,
Vol. 54,
Issue. 1,
p.
59.
DuBose, Derrick Albert
1992.
Determinacy and the sharp function on the reals.
Annals of Pure and Applied Logic,
Vol. 55,
Issue. 3,
p.
237.
DuBose, Derrick Albert
1992.
Determinacy and extended sharp functions on the reals, Part II: obtaining sharps from determinacy.
Annals of Pure and Applied Logic,
Vol. 58,
Issue. 1,
p.
1.
Cunningham, Daniel W.
1995.
The real core model and its scales.
Annals of Pure and Applied Logic,
Vol. 72,
Issue. 3,
p.
213.
1995.
1995 Annual Meeting of the Association for Symbol Logic.
Bulletin of Symbolic Logic,
Vol. 1,
Issue. 3,
p.
377.
Welch, P.D.
1996.
Determinacy in the difference hierarchy of co-analytic sets.
Annals of Pure and Applied Logic,
Vol. 80,
Issue. 1,
p.
69.
Larson, Paul B.
2012.
Sets and Extensions in the Twentieth Century.
Vol. 6,
Issue. ,
p.
457.
Friedman, Harvey M.
2017.
Logic Colloquium '01.
p.
151.
Le Sueur, Chris
2018.
Determinacy of refinements to the difference hierarchy of co-analytic sets.
Annals of Pure and Applied Logic,
Vol. 169,
Issue. 1,
p.
83.
Cheng, Yong
2019.
Incompleteness for Higher-Order Arithmetic.
p.
33.
Kechris, Alexander S.
Löwe, Benedikt
and
Steel, John R.
2020.
Large Cardinals, Determinacy and Other Topics.
Aguilera, J. P.
2025.
The metamathematics of separated determinacy.
Inventiones mathematicae,


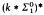 and
and 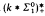 , which lie strictly between
, which lie strictly between 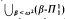 and
and 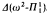 . We also define 0
. We also define 0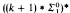 as well as the determinacy of
as well as the determinacy of 