Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-28T15:01:38.905Z Has data issue: false hasContentIssue false
  • English
  • Français

Equivalence between semantics for intuitionism. I

Published online by Cambridge University Press:  12 March 2014

E. G. K. López-Escobar
E. G. K. López-Escobar*
Affiliation:
University of Maryland, College Park, Maryland 20742
Get access Rights & Permissions [Opens in a new window]

Extract

It is probably because intuitionism is founded on the concept of (abstract) proof that it has been possible to develop various kinds of models. The following is but a partial list: Gabbay [5], Beth [2], Kripke [8], Kleene [7], Läuchli [9], McKinsey and Tarski [10], Rasiowa and Sikorski [14], Scott [15], de Swart [16], and Veldman [17].

The original purpose for having the models appears to have been for obtaining independence or consistency results for certain formalizations of intuitionism [see Beth [2], Prawitz [13]]; of course, if the models could be also justified as being plausible interpretations of intuitionistic thinking, so much the better. In fact, having some kind of plausible interpretation makes it much easier to work with the models. Occasionally the models were used to suggest possible extensions of the formal systems; for example, the Kripke models with constant domains have motivated interest in the formal logic CD which extends the Intuitionistic Predicate Calculus (IPC) by having the axiom schema

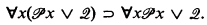
Type
Research Article
Information
The Journal of Symbolic Logic , Volume 46 , Issue 4 , December 1981 , pp. 773 - 780
Copyright
Copyright © Association for Symbolic Logic 1981

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Beth, E. W., Remarks on intuitionistic logic, Constructivity in mathematics, North-Holland, Amsterdam, 1957.Google Scholar
[2]Beth, E. W., The foundations of mathematics, North-Holland, Amsterdam, 1959.Google Scholar
[3]Caicedo, X., Back and forth in infinitary languages, Ph. D. thesis, University of Maryland, 1978.Google Scholar
[4]van Dalen, D., An interpretation of intuitionistic analysis, Annals of Mathematical Logic, vol. 13 (1978), pp. 1–43.CrossRefGoogle Scholar
[5]Gabbay, D., A new version of Beth semantics for intuitionistic logic, this Journal, vol. 42 (1977), pp. 306–308.Google Scholar
[6]de Jongh, D. H. J. and Smorynski, C., Kripke models and the intuitionistic theory of species, Annals of Mathematical Logic, vol. 9 (1976), pp. 157–186.CrossRefGoogle Scholar
[7]Kleene, S. C., On the interpretation of intuitionistic number theory, this Journal, vol. 10 (1945), pp. 109–124.Google Scholar
[8]Kripke, S., Semantical analysis of intuitionistic logic. I, Formal systems and recursive functions, (Crossley, and Dummett, , Editors), North-Holland, Amsterdam, 1963, pp. 92–130.Google Scholar
[9]Läuchli, H., An abstract notion of readability for which the intuitionistic predicate calculus is complete, Intuitionism and proof theory, (Kino, , Myhill, and Vesley, , Editors), North-Holland, Amsterdam, 1968.Google Scholar
[10]McKinsey, J. C. C., and Tarski, A., Some theorems about the sentential calculi of Lewis and Heyting, this Journal, vol. 13 (1948), pp. 1–15.Google Scholar
[11]MacLane, S., Categories for the working mathematician, Springer-Verlag, New York, 1971.Google Scholar
[12]Prawitz, D., Natural deduction, a proof-theoretical study, Almquist and Weksell, Stockholm, 1965.Google Scholar
[13]Prawitz, D., Some results for intuitionistic logic with second order quantification rules, Proof theory and Intuitionism (Kino, , Myhill, and Vesley, , Editors), North-Holland, Amsterdam, 1968.Google Scholar
[14]Rasiowa, H. and Sikorski, R., The mathematics of metamathematics, Pánstwowe Wydawnictwo Naukowe, Warsaw, 1963.Google Scholar
[15]Scott, D. S., Completeness proofs for the Intuitionistic sentential calculus, Summer Institute for Symbolic Logic, Cornell, 1957, second edition, 1960, Institute for Defense Analyses.Google Scholar
[16]de Swart, H., An intuitionistically plausible interpretation of intuitionistic logic, this Journal, vol. 42 (1977), pp. 564–578.Google Scholar
[17]Veldman, W., An intuitionistic completeness theorem for intuitionistic predicate logic, this Journal, vol. 41 (1976), pp. 159–166.Google Scholar