Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-22T20:26:26.975Z Has data issue: false hasContentIssue false
  • English
  • Français

Equational bases of boolean algebras

Published online by Cambridge University Press:  12 March 2014

F. M. Sioson
F. M. Sioson*
Affiliation:
University of Florida
Get access Rights & Permissions [Opens in a new window]

Extract

It is well-known that a Boolean algebra (B, +, ., ‐) may be defined as an algebraic system with at least two elements such that (for all x, y, z ε B):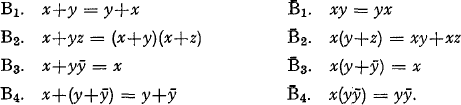

These axioms or equations are not independent, in the sense that some of them are logical consequences of the others. B. A. Bernstein [1] thought that the first three and their duals form an independent dual-symmetric definition of a Boolean algebra, but R. Montague and J. Tarski [3] proved later that B1 (or B̅1) follows from B2, B3, B̅1, B̅2, B̅3 (from B1, B2, B3, B̅2, B̅3).

Type
Articles
Information
The Journal of Symbolic Logic , Volume 29 , Issue 3 , September 1964 , pp. 115 - 124
Copyright
Copyright © Association for Symbolic Logic 1964

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Bernstein, B. A., A simplification of the Whitehead- Huntington set of postulates for Boolean algebras, Bulletin of the American Mathematical Society, vol. 22 (1916), pp. 458–459.CrossRefGoogle Scholar
[2]Bernstein, B. A., A dual-symmetric definition of Boolean algebra free from postulated special elements, Scripta mathematica, vol 16 (1950), pp. 157–160.Google Scholar
[3]Montague, R. and Tarski, J., On Bernstein's self-dual set of postulates for Boolean algebras, Proceedings of the American Mathematical Society, vol. 5 (1954), pp. 310–311.Google Scholar