Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-23T06:42:35.371Z Has data issue: false hasContentIssue false
  • English
  • Français

Equality in

Published online by Cambridge University Press:  12 March 2014

Jonathan P. Seldin
Jonathan P. Seldin*
Affiliation:
Southern Illinois University, Carbondale, Illinois 62901
Get access Rights & Permissions [Opens in a new window]

Extract

In [CLg. II, §15B6], the problem of representing equality in the system 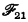by means of an ob Q is discussed; it is shown there that if Q is taken to be a canonical atom of degree 2 and if the axiom scheme

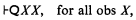
is postulated, then it follows by Rule Eq that

and, if no other properties are postulated for Q, then the converse of (1), Q-consistency, also holds. However, it is also desirable to have, in addition, the property

at least for some obs Z, and the statement is made in [CLg. II, §15B6] that no known way of incorporating this principle existed (at the time this statement was written) in such a way that there was a proof of Q-consistency. In this paper it is shown that if Z is restricted to be a basic canob of degree 1, i.e., if Z is restricted to be a predicate of one argument, then a system in which (2) is postulated can be proved Q-consistent.

The notations and conventions of [CLg. II] especially §15B, will be used throughout the paper.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 38 , Issue 4 , December 1973 , pp. 571 - 575
Copyright
Copyright © Association for Symbolic Logic 1973

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCE

[CLg. II] Curry, H. B., Hindley, J. R. and Seldin, J. P., Combinatory logic. Vol. 2, North-Holland, Amsterdam, 1972.Google Scholar