Published online by Cambridge University Press: 12 March 2014
Let ω be the nonnegative integers. G. E. Sacks once asked whether there exists an infinite X ⊆ ω such that, for all Y ⊆ X, ω1Yω1 where ω1 is the first nonrecursive ordinal. In this note we negatively answer this question by giving a simple proof that for every infinite set X ⊆ ω there exists Y ⊆ X such that 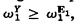 the first recursively inaccessible ordinal. This is accomplished by proving that Hα is hyper-arithmetic in Y whereHα is the αth hyperjump of the empty set ∅, defined in a suitable sense for all ordinals
the first recursively inaccessible ordinal. This is accomplished by proving that Hα is hyper-arithmetic in Y whereHα is the αth hyperjump of the empty set ∅, defined in a suitable sense for all ordinals 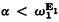
Background information and undefined notation can be found in Rogers [11]. In particular, we write A ≤hB(A ≤T B) if A is hyperarithmetical (recursive) in B, and A ≡hB if A ≤hB and B ≤hA. We will say that a set A is hyperarithmetically (recursively) encodable if, for every infinite set X ⊆ ω, there exists Y ⊆ X such that A ≤hY (A ≤TY). For any set A (hyperdegree a) let A′ (a′) denote the hyperjump of A (a). Let 0 denote the hyperdegree of ∅. A function f majorizes a function g if f(n) ≥ g(n) for every n. E1 is the representing (type-2) functional of
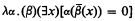
introduced by Tugué [13] (also Kleene [6]). Let 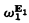 be the smallest ordinal which is not the order type of any well-ordering recursive in E1. Information on
be the smallest ordinal which is not the order type of any well-ordering recursive in E1. Information on 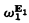 can be found in Richter [9] and [10].
can be found in Richter [9] and [10].