Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-19T02:17:23.327Z Has data issue: false hasContentIssue false
  • English
  • Français

Embedding the diamond in the Σ2 enumeration degrees

Published online by Cambridge University Press:  12 March 2014

Seema Ahmad
Seema Ahmad*
Affiliation:
IBM Canada Laboratory, North York, Ontario M3C 1H7, Canada
Get access Rights & Permissions [Opens in a new window]

Extract

Lachlan [5] has shown that it is not possible to embed the diamond lattice in the r.e. Turing degrees while preserving least and greatest elements; that is, there do not exist incomparable r.e. Turing degrees a and b such that a ∧ b = 0 and a ∨ b = 0′. Cooper [3] has compared the r.e. Turing degrees to the enumeration degrees below 0e′ and has asked if the two structures are elementarily equivalent.

In this paper we show that such an embedding is possible in the Σ2enumeration degrees, which implies a negative answer to Cooper's question.

Theorem. There are low enumeration degreesaandbsuch thata ∧ b = 0eanda ∨ b = 0e′.

Lower case italic letters denote elements of ω while upper case italic letters denote subsets of ω. D, E and F are reserved for finite sets, and K for 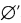′. If D = {x0, x1, …, xn} then the canonical index of D is 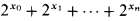, and the canonical index of 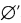is ∅. Dx denotes the set with canonical index x. {Wi}i∈ω is any fixed standard listing of the r.e. sets, and <·, ·> is any fixed recursive bijection from ω × ω to ω.

Intuitively, A is enumeration reducible to B if there is an effective algorithm for producing an enumeration of A from any enumeration of B. There is a natural one-to-one correspondence between all such algorithms and the r.e. sets.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 56 , Issue 1 , March 1991 , pp. 195 - 212
Copyright
Copyright © Association for Symbolic Logic 1991

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Cooper, S. B., Degrees of unsolvability complementary between recursively enumerable degrees. Part 1, Annals of Mathematical Logic, vol. 4 (1972), pp. 31–73.CrossRefGoogle Scholar
[2]Cooper, S. B., Partial degrees and the density problem, this Journal, vol. 47 (1982), pp. 854–859.Google Scholar
[3]Cooper, S. B., Partial degrees and the density problem. Part 2: The enumeration degrees of the Σ2 sets are dense, this Journal, vol. 49 (1984), pp. 503–513.Google Scholar
[4]Gutteridge, L., Some results on enumeration reducibility, Ph.D. Dissertation, Simon Fraser University, Burnaby, 1971.Google Scholar
[5]Lachlan, A. H., Lower bounds for pairs of recursively enumerable degrees, Proceedings of the London Mathematical Society, ser. 3, vol. 16 (1966), pp. 537–569.CrossRefGoogle Scholar
[6]McEvoy, K., Jumps of quasi-minimal enumeration degrees, this Journal, vol. 50 (1985), pp. 839–848.Google Scholar
[7]McEvoy, K. and Cooper, S. B., On minimal pairs of enumeration degrees, this Journal, vol. 50 (1985), pp. 983–1001.Google Scholar
[8]Rogers, H. Jr., Theory of recursive functions and effective computability, McGraw-Hill, New York, 1967.Google Scholar
[9]Soare, R. I., Recursively enumerable sets and degrees, Springer-Verlag, New York, 1987.CrossRefGoogle Scholar