Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-23T05:11:11.141Z Has data issue: false hasContentIssue false
  • English
  • Français

Effective operations in a general setting

Published online by Cambridge University Press:  12 March 2014

A. H. Lachlan
A. H. Lachlan*
Affiliation:
The University of Newcastle upon Tyne
Get access Rights & Permissions [Opens in a new window]

Extract

There are essentially two ‘positive’ results concerning the extension of effective operations to partial recursive functionals. The first proved by Myhill and Shepherdson in [9] states that any effective operation whose domain is the set of all partial recursive (p.r.) functions is potentially p.r. The second proved originally by Kreisel, Lacombe, and Shoenfield in [5] states: Let F be an effective operation mapping a set 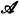of recursive functions into the natural numbers; if 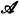has a recursively dense base, then F is potentially p.r. The main objective of this paper is to present these two theorems in a general setting.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 29 , Issue 4 , December 1964 , pp. 163 - 178
Copyright
Copyright © Association for Symbolic Logic 1964

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Čeitin, G. C., Algoritmičéskié operatory v konstruktivnyk polnyk séparabélnyk métričéskyk prostranstvak (Algorithmic operators on constructive complete separable metric spaces), Doklady Akadémii Nauk SSSR, vol. 128 (1959), pp. 49–52.Google Scholar
[2]Čeitin, G. C., Algoritmičéskié operatory v konstruktivnyk métričéskyk prostranstvak (Algorithmic operators on constructive metric spaces), Trudy matématičéskogo instituto imèni V. A. Stéklova, vol. 67 (1962), pp. 295–361.Google Scholar
[3]Gandy, R. O., Effective operations and recursive functionals, abstract, this Journal, vol. 27 (1962), pp. 378–379.Google Scholar
[4]Kleene, S. C., Introduction to Metamathematics, Amsterdam (North Holland), Groningen (Noordhoff), New York and Toronto (Van Nostrand), 1952, x + 550 p.Google Scholar
[5]Kreisel, G., Lacombe, D., and Shoenfield, J. R., Partial recursive functionals and effective operations, Constructivity in Mathematics, Amsterdam (North Holland), 1959, pp. 290–297.Google Scholar
[6]Lacombe, D., Extension de la notion de fonction récursive aux fonctions d'une ou plusieurs variables, Comptes Rendus de l'Académie des Sciences de Paris, vol. 240 (1955), pp. 2478–2480, and vol. 241 (1955), pp. 13–14, 151–153.Google Scholar
[7]Lacombe, D., Quelques procédés de definition en topologie récursive, Constructivity in Mathematics, Amsterdam (North Holland), 1959, pp. 129–158.Google Scholar
[8]Moschovakis, J. N., Recursive metric spaces, Ph.D. thesis, Part II, University of Wisconsin, 1963.Google Scholar
[9]Myhill, J. and Shepherdson, J. C., Effective operations on partial recursive functions, Zeitschrift für mathematische Logik und Grundlagen der Mathematik, vol. 1 (1955), pp. 310–317.CrossRefGoogle Scholar
[10]Nerode, A., Some Stone spaces and recursion theory, Duke Mathematical Journal, vol. 26 (1959), pp. 397–405.CrossRefGoogle Scholar
[11]Pour-El, M. B., Generalisation of a theorem of Kreisel, Lacombe, and Shoenfield, abstract, Notices of the American Mathematical Society, vol. 6 (1959), p. 528.Google Scholar
[12]Pour-El, M. B., A comparison of five computable operators, Zeitschrift für mathematische Logik und Grundlagen der Mathematik, vol. 6 (1960), pp. 325–340.CrossRefGoogle Scholar
[13]Rice, H. G., Classes of recursively enumerable sets and their decision problems, Transactions of the American Mathematical Society, vol. 74 (1953), pp. 358–366.CrossRefGoogle Scholar