No CrossRef data available.
Article contents
Dual easy uniformization and model-theoretic descriptive set theory
Published online by Cambridge University Press: 12 March 2014
Abstract
It is well known that, in the terminology of Moschovakis, Descriptive set theory (1980), every adequate normed pointclass closed under ∀ω has an effective version of the generalized reduction property (GRP) called the easy uniformization property (EUP). We prove a dual result: every adequate normed pointclass closed under ∃ω has the EUP. Moschovakis was concerned with the descriptive set theory of subsets of Polish topological spaces. We set up a general framework for parts of descriptive set theory and prove results that have as special cases not only the just-mentioned topological results, but also corresponding results concerning the descriptive set theory of classes of classes of structures.
Vaught (1973) asked whether the class of cPCδ classes of countable structures has the GRP. It does. A cPC(A) class is the class of all models of a sentence of the form 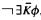 , where ϕ is a sentence of ℒ∞ω that is in A and
, where ϕ is a sentence of ℒ∞ω that is in A and 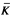 is a set of relation symbols that is in A. Vaught also asked whether there is any primitive recursively closed set A such that some effective version of the GRP holds for the class of cPC(A) classes of countable structures. There is: The class of cPC(A) classes of countable structures has the EUP if ω ∈ A and A is countable and primitive recursively closed. Those results and some extensions are obtained by first showing that the relevant classes of classes of structures, which Vaught showed normed, are in a suitable sense adequate and closed under ∃ω, and then applying the dual easy uniformization theorem.
is a set of relation symbols that is in A. Vaught also asked whether there is any primitive recursively closed set A such that some effective version of the GRP holds for the class of cPC(A) classes of countable structures. There is: The class of cPC(A) classes of countable structures has the EUP if ω ∈ A and A is countable and primitive recursively closed. Those results and some extensions are obtained by first showing that the relevant classes of classes of structures, which Vaught showed normed, are in a suitable sense adequate and closed under ∃ω, and then applying the dual easy uniformization theorem.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1991


