Published online by Cambridge University Press: 12 March 2014
It is a theorem of Rowbottom [12] that if κ is measurable and I is a normal prime ideal on κ, then for each λ < κ,
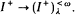
In this paper a natural structural property of ideals, distributivity, is considered and shown to be related to this and other ideal theoretic partition relations.
The set theoretical terminology is standard (see [7]) and background results on the theory of ideals may be found in [5] and [8]. Throughout κ will denote an uncountable regular cardinal, and I a proper, nonprincipal, κ-complete ideal on κ. NSκ is the ideal of nonstationary subsets of κ, and Iκ = {X ⊆ κ∣∣X∣<κ}. If A ∈ I+ (= P(κ) − I), then an I-partition of A is a maximal collection W ⊆, P(A) ∩ I+ so that X ∩ Y ∈ I whenever X, Y ∈ W, X ≠ Y. The I-partition W is said to be disjoint if distinct members of W are disjoint, and in this case, for 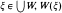 denotes the unique member of W containing ξ. A sequence 〈Wα ∣ α < η} of I-partitions of A is said to be decreasing if whenever α < β < η and X ∈ Wβ there is a Y ∈ Wα such that X ⊆ Y. (i.e., Wβ refines Wα).
denotes the unique member of W containing ξ. A sequence 〈Wα ∣ α < η} of I-partitions of A is said to be decreasing if whenever α < β < η and X ∈ Wβ there is a Y ∈ Wα such that X ⊆ Y. (i.e., Wβ refines Wα).