§1. Introduction. The basic problem of inner model theory is how to construct mice satisfying hypotheses appreciably stronger than “there is a Woodin limit of Woodin cardinals”. We have a family of constructions, the Kc-constructions, which ought to produce such mice under the appropriate hypotheses on V. Perhaps the most important thing we lack is a proof that the countable elementary submodels of premice produced by a Kc-construction are ω1 + 1-iterable. The best partial results in this direction are those of Neeman ([4]) for Kc-constructions making use of full background extenders over V, and those of Andretta, Neeman, and Steel ([1]) for arbitrary Kc-constructions.

Let 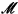be a countable premouse embedded by π into a level of the Kc-construction ℂ. If ℂ uses only full extenders over V as its background extenders, then π and ℂ enable one to lift an evolving iteration tree 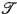on 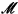to an iteration tree 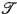* on V. (See [3, §12].) The good behavior of 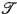* guarantees that of 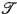. The natural conjecture here is that V is ω1 + 1-iterable with respect to such trees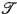* by the strategy of choosing the unique wellfounded branch. The open question here is uniqueness, since by [2] the uniqueness of the wellfounded branch chosen by 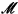* at limit stages strictly less than λ implies the existence of a wellfounded branch to be chosen at λ.