No CrossRef data available.
Published online by Cambridge University Press: 13 December 2024
We study the structure of infinite discrete sets D definable in expansions of ordered Abelian groups whose theories are strong and definably complete, with a particular emphasis on the set 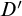 $D'$ comprised of differences between successive elements. In particular, if the burden of the structure is at most n, then the result of applying the operation
$D'$ comprised of differences between successive elements. In particular, if the burden of the structure is at most n, then the result of applying the operation  $D \mapsto D'\ n$ times must be a finite set (Theorem 1.1). In the case when the structure is densely ordered and has burden
$D \mapsto D'\ n$ times must be a finite set (Theorem 1.1). In the case when the structure is densely ordered and has burden 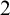 $2$, we show that any definable unary discrete set must be definable in some elementary extension of the structure
$2$, we show that any definable unary discrete set must be definable in some elementary extension of the structure  $\langle \mathbb{R}; <, +, \mathbb{Z} \rangle $ (Theorem 1.3).
$\langle \mathbb{R}; <, +, \mathbb{Z} \rangle $ (Theorem 1.3).