Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-16T15:29:08.322Z Has data issue: false hasContentIssue false
  • English
  • Français

Discontinuities of provably correct operators on the provably recursive real numbers

Published online by Cambridge University Press:  12 March 2014

William J. Collins  and
Paul Young
William J. Collins
Affiliation:
Salisbury State College, Salisbury, Maryland 21801
Paul Young*
Affiliation:
Purdue University, West Lafayette, Indiana 47907
*
University of Washington, Seattle, Washington 98195
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we continue, from [2], the development of provably recursive analysis, that is, the study of real numbers defined by programs which can be proven to be correct in some fixed axiom system S. In particular we develop the provable analogue of an effective operator on the set 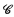of recursive real numbers, namely, a provably correct operator on the set 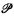of provably recursive real numbers. In Theorems 1 and 2 we exhibit a provably correct operator on 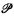which is discontinuous at 0; we thus disprove the analogue of the Ceitin-Moschovakis theorem of recursive analysis, which states that every effective operator on 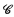is (effectively) continuous. Our final theorems show, however, that no provably correct operator on 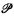can be proven (in S) to be discontinuous.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 48 , Issue 4 , December 1983 , pp. 913 - 920
Copyright
Copyright © Association for Symbolic Logic 1983

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Ceitin, G., Algorithmic operators in constructive complete separable metric spaces, Doklady Akademii Nauk SSSR, vol. 128 (1959), pp. 49–52. (Russian)Google Scholar
[2]Collins, W., Provably recursive real numbers, Notre Dame Journal of Formal Logic, vol. 19 (1978), pp. 513–522.CrossRefGoogle Scholar
[3]Collins, W., Provably recursive analysis, Ph.D. Dissertation, Purdue University (1973), pp. 1–141.Google Scholar
[4]Davis, M., Computability and unsolvability, McGraw-Hill, Inc., New York, 1958.Google Scholar
[5]Fischer, P., Theory of provable recursive functions, Transactions of the American Mathematical Society, vol. 117 (1965), pp. 494–520.CrossRefGoogle Scholar
[6]Kleene, S., Introduction to metamathematics, Van Nostrand, Princeton, N.J., 1952.Google Scholar
[7]Kleene, S. and Post, E., The upper semi-lattice of degrees of recursive unsolvability, Annals of Mathematics, vol. 59 (1954), pp. 379–407.CrossRefGoogle Scholar
[8]Kreisel, G., On the interpretation of non-finitist proofs, this Journal, vol. 16 (1951), pp. 241–247.Google Scholar
[9]Kreisel, G., On the interpretation of non-finitist proofs, this Journal, vol. 17 (1952), pp. 43–58.Google Scholar
[10]Markov, A., On constructive functions, American Mathematical Society Translations (2), vol. 29 (1963), pp. 163–196.Google Scholar
[11]Mazur, S., Computable analysis, Rosprawy Matematyczne, vol. 33 (1963).Google Scholar
[12]Moschovakis, Y., Recursive metric spaces, Fundamenta Mathematicae, vol. 55 (1964), pp. 215–238.CrossRefGoogle Scholar
[13]Ritchie, R. and Young, P. , Strong representability of partial functions in arithmetic theories, Information Sciences, vol. 1 (1969), pp. 189–204.CrossRefGoogle Scholar
[14]Young, P., Optimization among provably equivalent programs, Journal of the Association for Computing Machinery, vol. 24 (1977), pp. 693–700.CrossRefGoogle Scholar