Published online by Cambridge University Press: 07 September 2020
Consider a definably complete uniformly locally o-minimal expansion of the second kind of a densely linearly ordered abelian group. Let 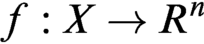 $f:X \rightarrow R^n$ be a definable map, where X is a definable set and R is the universe of the structure. We demonstrate the inequality
$f:X \rightarrow R^n$ be a definable map, where X is a definable set and R is the universe of the structure. We demonstrate the inequality 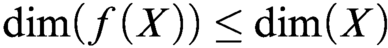 $\dim (f(X)) \leq \dim (X)$ in this paper. As a corollary, we get that the set of the points at which f is discontinuous is of dimension smaller than
$\dim (f(X)) \leq \dim (X)$ in this paper. As a corollary, we get that the set of the points at which f is discontinuous is of dimension smaller than 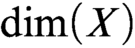 $\dim (X)$. We also show that the structure is definably Baire in the course of the proof of the inequality.
$\dim (X)$. We also show that the structure is definably Baire in the course of the proof of the inequality.