Published online by Cambridge University Press: 12 December 2014
We study the expressive power of independence-friendly quantifier prefixes composed of universal 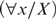 $\left( {\forall x/X} \right)$, existential
$\left( {\forall x/X} \right)$, existential  $\left( {\exists x/X} \right)$, and majority quantifiers
$\left( {\exists x/X} \right)$, and majority quantifiers  $\left( {Mx/X} \right)$. We provide four quantifier prefixes that can express NP hard properties and show that all quantifier prefixes capable of expressing NP-hard properties embed at least one of these four quantifier prefixes. As for the quantifier prefixes that do not embed any of these four quantifier prefixes, we show that they are equivalent to a first-order quantifier prefix composed of
$\left( {Mx/X} \right)$. We provide four quantifier prefixes that can express NP hard properties and show that all quantifier prefixes capable of expressing NP-hard properties embed at least one of these four quantifier prefixes. As for the quantifier prefixes that do not embed any of these four quantifier prefixes, we show that they are equivalent to a first-order quantifier prefix composed of  $\forall x$,
$\forall x$,  $\exists x$, and Mx. In unison, our results imply a dichotomy result: every independence-friendly quantifier prefix is either decidable in LOGSPACE or NP hard.
$\exists x$, and Mx. In unison, our results imply a dichotomy result: every independence-friendly quantifier prefix is either decidable in LOGSPACE or NP hard.