Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-23T06:53:53.786Z Has data issue: false hasContentIssue false
  • English
  • Français

Diagonals and 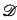-maximal sets

Published online by Cambridge University Press:  12 March 2014

Eberhard Herrmann  and
Martin Kummer
Eberhard Herrmann
Affiliation:
FB Mathematik, Humboldt-Universität, Berlin, Germany
Martin Kummer
Affiliation:
Institut Für Logik, Komplexität und deduktionssysteme, Universität Karlsdruhe, Karlsruhe, GermanyE-mail:, [email protected]
Get access Rights & Permissions [Opens in a new window]

Extract

In analogy to the definition of the halting problem K, an r.e. set A is called a diagonal iff there is a computable numbering ψ of the class of all partial recursive functions such that A = {i ∈ ω: ψi(i)↓} (in that case we say that A is the diagonal of ψ). This notion has been introduced in [10]. It captures all r.e. sets that can be constructed by diagonalization.

It was shown that any nonrecursive r.e. T-degree contains a diagonal, that for any diagonal A there is an r.e. nonrecursive nondiagonal B ≤TA, and that there are r.e. degrees a such that any r.e. set from a is a diagonal.

In §2 of the present paper we show that the property “A is a diagonal” is elementary lattice theoretic (e.l.t.). This result complements and generalizes previous results of Harrington and Lachlan, respectively. Harrington (see [16, XV. 1]) proved that the property of being the diagonal of some Gödelnumbering (i.e., of being creative) is e.l.t., and Lachlan [12] proved that the property of being a simple diagonal (i.e., of being simple and not hh-simple [10]) is e.l.t.

In §§3 and 4 we study the position of diagonals and nondiagonals inside the lattice of r.e. sets. We concentrate on an important class of nondiagonals, generalizing the maximal and hemimaximal sets: the 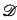-maximal sets. Using the results from [6] we are able to classify the 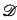-maximal sets that can be obtained as halfs of splittings of hh-simple sets.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 59 , Issue 1 , March 1994 , pp. 60 - 72
Copyright
Copyright © Association for Symbolic Logic 1994

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Degtev, A. N., Minimal 1-degrees and truth-table reducibility, Siberian Mathematical Journal, vol. 17 (1976), pp. 751–757.CrossRefGoogle Scholar
[2]Downey, R. G. and Stob, M., Automorphisms of the lattice of recursively enumerable sets: orbits, Advances in Mathematics, vol. 92 (1992), pp. 237–265.CrossRefGoogle Scholar
[3]Friedberg, R. M., Three theorems on recursive enumeration, this Journal, vol. 23 (1958), pp. 309–316.Google Scholar
[4]Monk, J.-D. (editor), Handbook of Boolean Algebras, Vol. 1–3, North-Holland, Amsterdam, 1989.Google Scholar
[5]Herrmann, E., Die Verbandseigenschaften der rekursiv aufzählbaren Mengen, Seminarberichte der Sektion Mathematik der Humboldt-Universität zu Berlin, Nr. 36, Berlin, 1981.Google Scholar
[6]Herrmann, E., Automorphisms of the lattice of recursively enumerable sets and hyperhypersimple sets, Proceedings of the Fourth Easter Conference on Model Theory (Köris, Groβ, 1986), pp. 68–108, Seminarberichte der Sektion Mathematik der Humboldt-Universität zu Berlin, Nr. 86, Berlin, 1986.Google Scholar
[7]Herrmann, E., Automorphisms of the lattice of recursively enumerable sets and hyperhypersimple sets, Logic, Methodology and Philosophy of Science, VIII (Moscow, 1987), Studies in Logic and the Foundations of Mathematics, vol. 126, North-Holland, Amsterdam, 1989, pp. 179–190.Google Scholar
[8]Kummer, M., An easy priority-free proof of a theorem of Friedberg, Theoretical Computer Science, vol. 74 (1990), pp. 249–251.CrossRefGoogle Scholar
[9]Kummer, M., Recursive enumeration without repetition revisited, Recursion theory week (K. Ambos-Spies, G. H. Müller, and G. E. Sacks, editors), Lecture Notes in Mathematics, vol. 1432, Springer-Verlag, Berlin, 1990, pp. 255–276.Google Scholar
[10]Kummer, M., Diagonals and semihyperhypersimple sets, this Journal, vol. 56 (1991), pp. 1068–1074.Google Scholar
[11]Lachlan, A. H., On the lattice of recursively enumerable sets, Transactions of the American Mathematical Society, vol. 130 (1968), pp. 1–37.CrossRefGoogle Scholar
[12]Lachlan, A. H., The elementary theory of recursively enumerable sets, Duke Mathematical Journal, vol. 35 (1968), pp. 123–146.CrossRefGoogle Scholar
[13]Lachlan, A. H., On some games which are relevant to the theory of recursively enumerable sets, Annals of Mathematics (2), vol. 91 (1970), pp. 291–310.CrossRefGoogle Scholar
[14]Lerman, M. and Soare, R. I., A decidable fragment of the lattice of recursively enumerable sets, Transactions of the American Mathematical Society, vol. 257 (1980), pp. 1–37.CrossRefGoogle Scholar
[15]Maass, W. and Stob, M., The intervals of the lattice of recursively enumerable sets determined by major subsets, Annals of Pure and Applied Logic, vol. 24 (1983), pp. 189–212.CrossRefGoogle Scholar
[16]Soare, R. I., Recursively enumerable sets and degrees, Springer-Verlag, Berlin, 1987.CrossRefGoogle Scholar