Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Kechris, Alexander S.
Solovay, Robert M.
and
Steel, John R.
1981.
Cabal Seminar 77 – 79.
Vol. 839,
Issue. ,
p.
101.
Kanovei, V. G.
1988.
The axiom of determinacy and the modern development of descriptive set theory.
Journal of Soviet Mathematics,
Vol. 40,
Issue. 3,
p.
257.
Louveau, Alain
1992.
Set Theory of the Continuum.
Vol. 26,
Issue. ,
p.
103.
Addison, J.W.
2004.
Tarski's theory of definability: common themes in descriptive set theory, recursive function theory, classical pure logic, and finite-universe logic.
Annals of Pure and Applied Logic,
Vol. 126,
Issue. 1-3,
p.
77.
Selivanov, V. L.
2005.
Classifying countable Boolean terms.
Algebra and Logic,
Vol. 44,
Issue. 2,
p.
95.
Jackson, Steve
2010.
Logic Colloquium 2007.
p.
92.
Jackson, Steve
2010.
Handbook of Set Theory.
p.
1753.
Wadge, William W.
2011.
Wadge Degrees and Projective Ordinals The Cabal Seminar Volume II.
p.
166.
Kechris, Alexander S.
Solovay, Robert M.
and
Steel, John R.
2011.
Wadge Degrees and Projective Ordinals The Cabal Seminar Volume II.
p.
118.
Andretta, Alessandro
and
Louveau, Alain
2011.
Wadge Degrees and Projective Ordinals The Cabal Seminar Volume II.
p.
3.
Louveau, Alain
2011.
Wadge Degrees and Projective Ordinals The Cabal Seminar Volume II.
p.
47.
Steel, John R.
2011.
Wadge Degrees and Projective Ordinals The Cabal Seminar Volume II.
p.
102.
Apter, Arthur
Jackson, Stephen
and
Löwe, Benedikt
2012.
Cofinality and measurability of the first three uncountable cardinals.
Transactions of the American Mathematical Society,
Vol. 365,
Issue. 1,
p.
59.
Larson, Paul B.
2012.
Sets and Extensions in the Twentieth Century.
Vol. 6,
Issue. ,
p.
457.
Andretta, Alessandro
and
Camerlo, Riccardo
2019.
Analytic sets of reals and the density function in the Cantor space.
European Journal of Mathematics,
Vol. 5,
Issue. 1,
p.
49.
Kechris, Alexander S.
Löwe, Benedikt
and
Steel, John R.
2020.
Large Cardinals, Determinacy and Other Topics.
Kanovei, Vladimir Grigorevich
and
Lyubetskii, Vasilii Aleksandrovich
2021.
Модели теории множеств, в которых теорема отделимости неверна.
Известия Российской академии наук. Серия математическая,
Vol. 85,
Issue. 6,
p.
164.
Kanovei, V. G.
and
Lyubetsky, V. A.
2021.
Models of set theory in which the separation theorem fails.
Izvestiya: Mathematics,
Vol. 85,
Issue. 6,
p.
1181.
Kihara, Takayuki
2022.
Topological reducibilities for discontinuous functions and their structures.
Israel Journal of Mathematics,
Vol. 252,
Issue. 1,
p.
461.
Kanovei, Vladimir
and
Lyubetsky, Vassily
2022.
A Model in Which the Separation Principle Holds for a Given Effective Projective Sigma-Class.
Axioms,
Vol. 11,
Issue. 3,
p.
122.
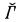 is {~A∣ A ∈ Γ}. (Complements are relative to ωω.) If Γ is nonselfdual, i.e.
is {~A∣ A ∈ Γ}. (Complements are relative to ωω.) If Γ is nonselfdual, i.e. 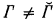 , then let
, then let 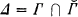 . We say a nonselfdual pointclass Γ has the first separation property, and write Sep(Γ), iff (∀A, B ∈ Γ)(A ⋂ B = ∅ ⇒ (∃C ∈ Δ)(A ⊆ C ∧ B ⋂ = ∅)). The set C is said to separate A and B.
. We say a nonselfdual pointclass Γ has the first separation property, and write Sep(Γ), iff (∀A, B ∈ Γ)(A ⋂ B = ∅ ⇒ (∃C ∈ Δ)(A ⊆ C ∧ B ⋂ = ∅)). The set C is said to separate A and B.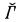 ) holds. Van Wesep [2] provides a partial explanation of this fact by showing that, assuming the full axiom of determinateness, one of Sep(Γ) and Sep(
) holds. Van Wesep [2] provides a partial explanation of this fact by showing that, assuming the full axiom of determinateness, one of Sep(Γ) and Sep(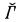 ) must fail for all nonselfdual pointclasses Γ. We shall complete the explanation by showing that one of Sep(Γ) and Sep(
) must fail for all nonselfdual pointclasses Γ. We shall complete the explanation by showing that one of Sep(Γ) and Sep(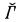 ) must hold.
) must hold.