Article contents
The Determinacy of Context-Free Games
Published online by Cambridge University Press: 12 March 2014
Abstract
We prove that the determinacy of Gale-Stewart games whose winning sets are accepted by realtime 1-counter Büchi automata is equivalent to the determinacy of (effective) analytic Gale-Stewart games which is known to be a large cardinal assumption. We show also that the determinacy of Wadge games between two players in charge of ω-languages accepted by 1-counter Büchi automata is equivalent to the (effective) analytic Wadge determinacy. Using some results of set theory we prove that one can effectively construct a 1-counter Büchi automaton 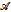 and a Büchi automaton
and a Büchi automaton 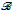 such that: (1) There exists a model of ZFC in which Player 2 has a winning strategy in the Wadge game W(L(
such that: (1) There exists a model of ZFC in which Player 2 has a winning strategy in the Wadge game W(L(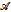 ), L(
), L(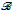 )); (2) There exists a model of ZFC in which the Wadge game W(L(
)); (2) There exists a model of ZFC in which the Wadge game W(L(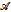 ), L(
), L(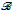 )) is not determined. Moreover these are the only two possibilities, i.e. there are no models of ZFC in which Player 1 has a winning strategy in the Wadge game W(L(
)) is not determined. Moreover these are the only two possibilities, i.e. there are no models of ZFC in which Player 1 has a winning strategy in the Wadge game W(L(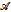 ), L(
), L(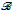 )).
)).
Keywords
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2013
References
REFERENCES
- 5
- Cited by


