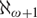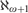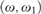Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Rinot, Assaf
2022.
On the ideal J[κ].
Annals of Pure and Applied Logic,
Vol. 173,
Issue. 2,
p.
103055.
Honzik, Radek
Lambie-Hanson, Chris
and
Stejskalová, Šárka
2024.
Indestructibility of some compactness principles over models of PFA.
Annals of Pure and Applied Logic,
Vol. 175,
Issue. 1,
p.
103359.