No CrossRef data available.
Article contents
DESCRIPTIVE PROPERTIES OF I2-EMBEDDINGS
Published online by Cambridge University Press: 27 January 2025
Abstract
We contribute to the study of generalizations of the Perfect Set Property and the Baire Property to subsets of spaces of higher cardinalities, like the power set 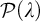 ${\mathcal {P}}({\lambda })$ of a singular cardinal
${\mathcal {P}}({\lambda })$ of a singular cardinal 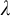 $\lambda $ of countable cofinality or products
$\lambda $ of countable cofinality or products 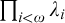 $\prod _{i<\omega }\lambda _i$ for a strictly increasing sequence
$\prod _{i<\omega }\lambda _i$ for a strictly increasing sequence 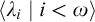 $\langle {\lambda _i}~\vert ~{i<\omega }\rangle $ of cardinals. We consider the question under which large cardinal hypothesis classes of definable subsets of these spaces possess such regularity properties, focusing on rank-into-rank axioms and classes of sets definable by
$\langle {\lambda _i}~\vert ~{i<\omega }\rangle $ of cardinals. We consider the question under which large cardinal hypothesis classes of definable subsets of these spaces possess such regularity properties, focusing on rank-into-rank axioms and classes of sets definable by 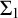 $\Sigma _1$-formulas with parameters from various collections of sets. We prove that
$\Sigma _1$-formulas with parameters from various collections of sets. We prove that 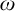 $\omega $-many measurable cardinals, while sufficient to prove the perfect set property of all
$\omega $-many measurable cardinals, while sufficient to prove the perfect set property of all 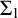 $\Sigma _1$-definable sets with parameters in
$\Sigma _1$-definable sets with parameters in 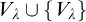 $V_\lambda \cup \{V_\lambda \}$, are not enough to prove it if there is a cofinal sequence in
$V_\lambda \cup \{V_\lambda \}$, are not enough to prove it if there is a cofinal sequence in 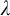 $\lambda $ in the parameters. For this conclusion, the existence of an I2-embedding is enough, but there are parameters in
$\lambda $ in the parameters. For this conclusion, the existence of an I2-embedding is enough, but there are parameters in 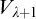 $V_{\lambda +1}$ for which I2 is still not enough. The situation is similar for the Baire property: under I2 all sets that are
$V_{\lambda +1}$ for which I2 is still not enough. The situation is similar for the Baire property: under I2 all sets that are 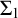 $\Sigma _1$-definable using elements of
$\Sigma _1$-definable using elements of 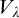 $V_\lambda $ and a cofinal sequence as parameters have the Baire property, but I2 is not enough for some parameter in
$V_\lambda $ and a cofinal sequence as parameters have the Baire property, but I2 is not enough for some parameter in 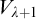 $V_{\lambda +1}$. Finally, the existence of an I0-embedding implies that all sets that are
$V_{\lambda +1}$. Finally, the existence of an I0-embedding implies that all sets that are 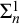 $\Sigma ^1_n$-definable with parameters in
$\Sigma ^1_n$-definable with parameters in 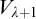 $V_{\lambda +1}$ have the Baire property.
$V_{\lambda +1}$ have the Baire property.
- Type
- Article
- Information
- Copyright
- © The Author(s), 2025. Published by Cambridge University Press on behalf of The Association for Symbolic Logic



