Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-24T23:50:21.302Z Has data issue: false hasContentIssue false
  • English
  • Français

Descriptive complexity of finite structures: Saving the quantifier rank

Published online by Cambridge University Press:  12 March 2014

Oleg Pikhurko  and
Oleg Verbitsky
Oleg Pikhurko
Affiliation:
Department of Mathematical Sciences, Carnegie Mellon University, Pittsburgh, Pennsylvania 15213-3890, USA, URL: http://www.math.cmu.edu/~pikhurko/
Oleg Verbitsky
Affiliation:
Department of Mechanics and Mathematics, Kyiv National University, Kyiv 01033., Ukraine, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We say that a first order formula Φ distinguishes a structure M over a vocabulary L from another structure M′ over the same vocabulary if Φ is true on M but false on M′. A formula Φ defines an L-structure M if Φ distinguishes M from any other non-isomorphic L-structure M′. A formula Φ identifies an n-element L-structure M if Φ distinguishes M from any other non-isomorphic n-element L-structure M′.

We prove that every n-element structure M is identifiable by a formula with quantifier rank less than 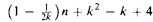and at most one quantifier alternation, where k is the maximum relation arity of M. Moreover, if the automorphism group of M contains no transposition of two elements, the same result holds for definability rather than identification.

The Bernays-Schönfinkel class consists of prenex formulas in which the existential quantifiers all precede the universal quantifiers. We prove that every n-element structure M is identifiable by a formula in the Bernays-Schönfinkel class with less than 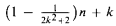quantifiers. If in this class of identifying formulas we restrict the number of universal quantifiers to k, then less than 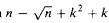quantifiers suffice to identify M and. as long as we keep the number of universal quantifiers bounded by a constant, at total 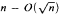quantifiers are necessary.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 70 , Issue 2 , June 2005 , pp. 419 - 450
Copyright
Copyright © Association for Symbolic Logic 2005

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Börger, E., Grädel, E., and Gurevich, Y., The classical decision problem, Springer-Verlag, 1997.Google Scholar
[2] Cai, J.-Y., Fürer, M., and Immerman, N., An optimal lower bound on the number of variables for graph identification, Combinatorica, vol. 12 (1992), pp. 389–410.Google Scholar
[3] Ebbinghaus, H.-D. and Flum, J., Finite model theory, 2nd rev. ed., Springer-Verlag, 1999.Google Scholar
[4] Ehrenfeucht, A., An application of games to the completeness problem for formalized theories, Fundamenta Mathematicae, vol. 49 (1961), pp. 129–141.Google Scholar
[5] Fagin, R., Finite-model theory—a personal perspective, Theoretical Computer Science, vol. 116 (1993), pp. 3–31.CrossRefGoogle Scholar
[6] Fraïssé, R., Sur quelques classifications des systems de relations, Université d'Alger, Publications Scientifiques, Serie A, vol. 1 (1954), pp. 35–182.Google Scholar
[7] Grohe, M., Fixed-point logics on planar graphs, Proceedings of the Annual Conference on Logic in Computer Science, 1998, pp. 6–15.Google Scholar
[8] Grohe, M., isomorphism testing for embeddable graphs through definability, Proceedings of the 32nd ACM Annual Symposium on Theory of Computing (STOC), 2000, pp. 63–72.Google Scholar
[9] Immerman, N., Descriptive complexity, Springer-Verlag, 1999.Google Scholar
[10] Immerman, N. and Kozen, D., Definability with bounded number of bound variables, Information and Computation, vol. 83 (1989), pp. 121–139.CrossRefGoogle Scholar
[11] Immerman, N. and Lander, E., Describing graphs: a first-order approach to graph canonization, Complexity theory retrospective (Selman, A., editor), Springer-Verlag, 1990, pp. 59–81.Google Scholar
[12] Kim, J. H., Pikhurko, O., Spencer, J., and Verbitsky, O., How complex are random graphs in first order logic?, to appear in Random Structures and Algorithms, E-print http://arxiv.org/abs/math.C0/0401247, 2004.Google Scholar
[13] Pezzoli, E., Computational complexity of Ehrenfeucht-Fraïssé games on finite structures, Proceedings of the CSL '98 conference (Gottlob, G. and Seyr, K., editors). Lecture Notes in Computer Science, vol. 1584, Springer-Verlag, 1999, pp. 159–170.Google Scholar
[14] Pikhurko, O., Spencer, J., and Verbitsky, O., Succinct definitions in first order graph theory, submitted, E-print http://arxiv.org/abs/math.C0/0401307, 2004.Google Scholar
[15] Pikhurko, O., Veith, H., and Verbitsky, O., First order definability of graphs: tight bounds on quantifier rank, submitted, E-print http://arxiv.org/abs/math.C0/0311041, 2003.Google Scholar
[16] Pikhurko, O. and Verbitsky, O., Descriptive complexity of finite structures: saving the quantifier rank, E-print http.-//arxiv.org/abs/math.L0/0305244, 2003.Google Scholar
[17] Spencer, J., The strange logic of random graphs, Springer-Verlag, 2001.Google Scholar