Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Jockusch, Carl G.
and
Posner, David B.
1981.
Automorphism bases for degrees of unsolvability.
Israel Journal of Mathematics,
Vol. 40,
Issue. 2,
p.
150.
Chong, C. T.
and
Jockusch, C. G.
1984.
Computation and Proof Theory.
Vol. 1104,
Issue. ,
p.
63.
Lerman, Manuel
1985.
Recursion Theory Week.
Vol. 1141,
Issue. ,
p.
260.
Lerman, M.
1985.
Upper bounds for the arithmetical degrees.
Annals of Pure and Applied Logic,
Vol. 29,
Issue. 3,
p.
225.
Kučera, Antonín
1985.
Recursion Theory Week.
Vol. 1141,
Issue. ,
p.
245.
Chong, C.T.
1986.
1-Generic degrees and minimal degrees in higher recursion theory, II.
Annals of Pure and Applied Logic,
Vol. 31,
Issue. ,
p.
165.
Cooper, S.Barry
and
Epstein, Richard L.
1987.
Complementing below recursively enumerable degrees.
Annals of Pure and Applied Logic,
Vol. 34,
Issue. 1,
p.
15.
Kučera, Antonín
1987.
Logic Colloquium '86, Proceedings of the Colloquium held in Hull.
Vol. 124,
Issue. ,
p.
133.
CHONG, C. T.
1987.
1-Generic degrees and minimal degrees in higher recursion theory.
Japanese journal of mathematics. New series,
Vol. 13,
Issue. 2,
p.
381.
Slaman, Theodore A.
and
Steel, John R.
1988.
Cabal Seminar 81–85.
Vol. 1333,
Issue. ,
p.
37.
Lerman, Manuel
and
Shore, Richard A.
1988.
Decidability and invariant classes for degree structures.
Transactions of the American Mathematical Society,
Vol. 310,
Issue. 2,
p.
669.
Cooper, S. Barry
1990.
The jump is definable in the structure of the degrees of unsolvability.
Bulletin of the American Mathematical Society,
Vol. 23,
Issue. 1,
p.
151.
Jockusch, Carl
and
Stephan, Frank
1993.
A cohesive set which is not high.
Mathematical Logic Quarterly,
Vol. 39,
Issue. 1,
p.
515.
Cooper, S.Barry
Sorbi, Andrea
and
Yi, Xiaoding
1996.
Cupping and noncupping in the enumeration degrees of ∑20 sets.
Annals of Pure and Applied Logic,
Vol. 82,
Issue. 3,
p.
317.
Stephan, Frank
1998.
Learning via queries and oracles.
Annals of Pure and Applied Logic,
Vol. 94,
Issue. 1-3,
p.
273.
Cooper, S. Barry
1999.
Handbook of Computability Theory.
Vol. 140,
Issue. ,
p.
121.
Sh. KALIMULLIN, I.
2003.
DEFINABILITY OF THE JUMP OPERATOR IN THE ENUMERATION DEGREES.
Journal of Mathematical Logic,
Vol. 03,
Issue. 02,
p.
257.
Jockusch, Carl
Li, Angsheng
and
Yang, Yue
2004.
A join theorem for the computably enumerable degrees.
Transactions of the American Mathematical Society,
Vol. 356,
Issue. 7,
p.
2557.
Lewis, Andrew
2004.
Finite cupping sets.
Archive for Mathematical Logic,
Vol. 43,
Issue. 7,
p.
845.
Wu, Guohua
2004.
Quasi‐complements of the cappable degrees.
Mathematical Logic Quarterly,
Vol. 50,
Issue. 2,
p.
189.


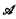 and
and 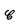 are sets of degrees uniformly recursive in
are sets of degrees uniformly recursive in 