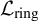1 Introduction
Many successful investigations around the existence and properties of solutions of polynomial equations over a field rely on enriching the field with a valuation. For example, over the field of
![]() $p$
-adic numbers
$p$
-adic numbers
![]() $\mathbb Q_p$
the valuation ring is an
$\mathbb Q_p$
the valuation ring is an
![]() $\mathcal {L}_{\mathrm {ring}}$
-definable subset, as first observed in the seminal work of Julia Robinson on Hilbert’s Tenth Problem [Reference Robinson, Addison, Henkin and Tarski20]. Understanding this phenomenon is a classical topic in the model theory of valued fields, and it has striking applications in the investigations around dividing lines for fields, see, e.g., Johnson’s spectacular classification of dp-finite fields in [Reference Johnson12]. For a more thorough survey on definability of valuations, we refer the reader to [Reference Fehm and Jahnke6].
$\mathcal {L}_{\mathrm {ring}}$
-definable subset, as first observed in the seminal work of Julia Robinson on Hilbert’s Tenth Problem [Reference Robinson, Addison, Henkin and Tarski20]. Understanding this phenomenon is a classical topic in the model theory of valued fields, and it has striking applications in the investigations around dividing lines for fields, see, e.g., Johnson’s spectacular classification of dp-finite fields in [Reference Johnson12]. For a more thorough survey on definability of valuations, we refer the reader to [Reference Fehm and Jahnke6].
In this manuscript, we will focus on the problem of characterizing which fields admit a non-trivial definable henselian valuation. There are some clear obstructions: for example, if the field is separably closed, then the answer is always no. Once this case is excluded, Jahnke and Koenigsmann isolate in [Reference Jahnke and Koenigsmann10] necessary and sufficient properties of the canonical henselian valuation
![]() $v_K$
of a field
$v_K$
of a field
![]() $K$
(see Subsection 2.3) for the existence of a definable non-trivial henselian valuation, under the assumption that
$K$
(see Subsection 2.3) for the existence of a definable non-trivial henselian valuation, under the assumption that
![]() $\operatorname {\mathrm {char}}{Kv_K} = 0$
.
$\operatorname {\mathrm {char}}{Kv_K} = 0$
.
Theorem 1.1 [Reference Jahnke and Koenigsmann10, Corollary 6.1].
Let
![]() $K$
be a henselian field that is not separably closed, with
$K$
be a henselian field that is not separably closed, with
![]() $\operatorname {\mathrm {char}}{Kv_K} = 0$
. Then
$\operatorname {\mathrm {char}}{Kv_K} = 0$
. Then
![]() $K$
admits a definable non-trivial henselian valuation if and only if at least one of the following conditions holds:
$K$
admits a definable non-trivial henselian valuation if and only if at least one of the following conditions holds:
-
(1)
 $Kv_K$
is separably closed,
$Kv_K$
is separably closed, -
(2)
 $Kv_K$
is not t-henselian,
$Kv_K$
is not t-henselian, -
(3) there is
 $L \succeq Kv_K$
such that
$L \succeq Kv_K$
such that
 $v_LL$
is not divisible,
$v_LL$
is not divisible, -
(4)
 $v_KK$
is not divisible.
$v_KK$
is not divisible.
This characterization (and its extension, which we will state in a moment) falls into the general philosophy of Ax-Kochen/Ershov principles. Typically, (model-theoretic) questions about a valued field
![]() $(K,v)$
are answered using its residue field
$(K,v)$
are answered using its residue field
![]() $Kv$
and its value group
$Kv$
and its value group
![]() $vK$
. In this case, since the question is about a field
$vK$
. In this case, since the question is about a field
![]() $K$
with no specified valuation, one ought to isolate a canonical one among all its henselian valuations; this is usually denoted by
$K$
with no specified valuation, one ought to isolate a canonical one among all its henselian valuations; this is usually denoted by
![]() $v_K$
. Answers to model-theoretic questions about
$v_K$
. Answers to model-theoretic questions about
![]() $K$
, then, should be given in terms of properties of
$K$
, then, should be given in terms of properties of
![]() $Kv_K$
and
$Kv_K$
and
![]() $v_KK$
.
$v_KK$
.
1.1 Our result
We extend the result of Jahnke and Koenigsmann by removing the assumption on the residue characteristic.
Main theorem. Let
![]() $K$
be perfect, not separably closed, and henselian. If
$K$
be perfect, not separably closed, and henselian. If
![]() ${\operatorname {\mathrm {char}}{K} = 0}$
and
${\operatorname {\mathrm {char}}{K} = 0}$
and
![]() ${\operatorname {\mathrm {char}}{Kv_K} = p> 0}$
, assume that
${\operatorname {\mathrm {char}}{Kv_K} = p> 0}$
, assume that
![]() $\mathcal {O}_{v_K}/p$
is semi-perfect. Then
$\mathcal {O}_{v_K}/p$
is semi-perfect. Then
![]() $K$
admits a definable non-trivial henselian valuation if and only if at least one of the following conditions hold:
$K$
admits a definable non-trivial henselian valuation if and only if at least one of the following conditions hold:
-
(1)
 $Kv_K$
is separably closed,
$Kv_K$
is separably closed, -
(2)
 $Kv_K$
is not t-henselian,
$Kv_K$
is not t-henselian, -
(3) there is
 $L \succeq Kv_K$
such that
$L \succeq Kv_K$
such that
 $v_LL$
is not divisible,
$v_LL$
is not divisible, -
(4)
 $v_KK$
is not divisible,
$v_KK$
is not divisible, -
(5)
 $(K,v_K)$
is not defectless,
$(K,v_K)$
is not defectless, -
(6) there is
 $L \succeq Kv_K$
such that
$L \succeq Kv_K$
such that
 $(L,v_L)$
is not defectless.
$(L,v_L)$
is not defectless.
Remark 1.2. Note that in conditions 3 and 6, one automatically has that
![]() $v_L$
is non-trivial (since the trivial valuation has divisible value group, and is defectless). Moreover, conditions 5 and 6 are trivial when
$v_L$
is non-trivial (since the trivial valuation has divisible value group, and is defectless). Moreover, conditions 5 and 6 are trivial when
![]() $\operatorname {\mathrm {char}}{Kv_K} = 0$
(for condition 6, see Corollary 2.3), and thus in that case the theorem reduces to Theorem 1.1.
$\operatorname {\mathrm {char}}{Kv_K} = 0$
(for condition 6, see Corollary 2.3), and thus in that case the theorem reduces to Theorem 1.1.
The paper is structured as follows:
-
• Section 2 sets the stage, by fixing the notation and a few elementary facts.
-
• Section 3 explores the two roles played by divisibility of the value group: on the one hand, in Proposition 3.6, failure of divisibility in an elementary extension of
 $Kv_K$
is exploited to (
$Kv_K$
is exploited to (
 $\varnothing $
-)define a valuation; on the other, in Theorem 3.5, divisibility is the keystone to finding obstructions to the existence of definable valuations.
$\varnothing $
-)define a valuation; on the other, in Theorem 3.5, divisibility is the keystone to finding obstructions to the existence of definable valuations. -
• Section 4 deploys the technology of independent defect to build definable henselian valuations from certain kinds of Galois defect extensions.
-
• Section 5 puts everything together, providing the full characterization as advertised.
-
• Section 6 provides a few explicit examples of fields that fit into the main result, and discusses a few open questions.
2 Preliminaries
2.1 Notation
Given a valued field
![]() $(K,v)$
, we denote by
$(K,v)$
, we denote by
![]() $\mathcal {O}_v$
or
$\mathcal {O}_v$
or
![]() $\mathcal {O}_{(K,v)}$
its valuation ring with maximal ideal
$\mathcal {O}_{(K,v)}$
its valuation ring with maximal ideal
![]() $\mathfrak m_v$
,
$\mathfrak m_v$
,
![]() $Kv$
its residue field and
$Kv$
its residue field and
![]() $vK$
its value group. We will write
$vK$
its value group. We will write
![]() ${vK}_{\infty }$
for
${vK}_{\infty }$
for
![]() $vK \cup \{\infty \}$
, and denote by
$vK \cup \{\infty \}$
, and denote by
![]() $\operatorname {res}_v\colon \mathcal {O}_v \to Kv$
the residue map. Given a field
$\operatorname {res}_v\colon \mathcal {O}_v \to Kv$
the residue map. Given a field
![]() $K$
, we denote its separable closure by
$K$
, we denote its separable closure by
![]() $K^{\mathrm {sep}}$
. A field will be called henselian if it admits a non-trivial henselian valuation. A ring of characteristic
$K^{\mathrm {sep}}$
. A field will be called henselian if it admits a non-trivial henselian valuation. A ring of characteristic
![]() $p>0$
is called semi-perfect if
$p>0$
is called semi-perfect if
![]() $x \mapsto x^p$
is surjective (but not necessarily injective). If
$x \mapsto x^p$
is surjective (but not necessarily injective). If
![]() $K \subseteq L$
is a Galois extension, we will write
$K \subseteq L$
is a Galois extension, we will write
![]() ${\operatorname {Gal}(L | K)}$
for the corresponding Galois group. We will mostly work with the two languages
${\operatorname {Gal}(L | K)}$
for the corresponding Galois group. We will mostly work with the two languages
![]() $\mathcal {L}_{\mathrm {ring}} = \{+,\;\cdot \;,0,1\}$
, and
$\mathcal {L}_{\mathrm {ring}} = \{+,\;\cdot \;,0,1\}$
, and
![]() $\mathcal {L}_{\mathrm {val}} = \mathcal {L}_{\mathrm {ring}} \cup \{\mathcal {O}\}$
, where
$\mathcal {L}_{\mathrm {val}} = \mathcal {L}_{\mathrm {ring}} \cup \{\mathcal {O}\}$
, where
![]() $\mathcal {O}$
is a unary predicate. If
$\mathcal {O}$
is a unary predicate. If
![]() $M$
is a first-order structure,
$M$
is a first-order structure,
![]() $I$
is an index set and
$I$
is an index set and
![]() $\mathcal U$
is an ultrafilter on
$\mathcal U$
is an ultrafilter on
![]() $I$
, then we denote by
$I$
, then we denote by
![]() $M^{\mathcal U}$
the corresponding ultrapower. Unless otherwise stated, definable will mean definable with parameters. Otherwise, we say
$M^{\mathcal U}$
the corresponding ultrapower. Unless otherwise stated, definable will mean definable with parameters. Otherwise, we say
![]() $\varnothing $
-definable.
$\varnothing $
-definable.
2.2 Coarsenings and compositions
We briefly recall some facts about coarsenings and refinements of valuations, which are explained in greater depth in [Reference Engler and Prestel4, Section 2.3]. For two valuations
![]() $v$
and
$v$
and
![]() $w$
on
$w$
on
![]() $K$
, we say that
$K$
, we say that
![]() $v$
is finer than
$v$
is finer than
![]() $w$
or is a refinement of
$w$
or is a refinement of
![]() $w$
(that
$w$
(that
![]() $w$
is coarser than
$w$
is coarser than
![]() $v$
or is a coarsening of
$v$
or is a coarsening of
![]() $v$
), if
$v$
), if
![]() $\mathcal {O}_v \subseteq \mathcal {O}_w$
. We identify
$\mathcal {O}_v \subseteq \mathcal {O}_w$
. We identify
![]() $v$
and
$v$
and
![]() $w$
if they have the same valuation ring, and use
$w$
if they have the same valuation ring, and use
![]() $v$
and
$v$
and
![]() $\mathcal {O}_v$
interchangeably. We say
$\mathcal {O}_v$
interchangeably. We say
![]() $v$
and
$v$
and
![]() $w$
are comparable if
$w$
are comparable if
![]() $v$
is a coarsening of
$v$
is a coarsening of
![]() $w$
, or
$w$
, or
![]() $w$
is a coarsening of
$w$
is a coarsening of
![]() $v$
. Coarsenings of a fixed valuation ring
$v$
. Coarsenings of a fixed valuation ring
![]() $\mathcal {O}_v$
are linearly ordered by inclusion and in one-to-one correspondence with convex subgroups of
$\mathcal {O}_v$
are linearly ordered by inclusion and in one-to-one correspondence with convex subgroups of
![]() $vK$
. We denote by
$vK$
. We denote by
![]() $v_H$
the coarsening of
$v_H$
the coarsening of
![]() $v$
associated with a convex subgroup
$v$
associated with a convex subgroup
![]() $H$
of
$H$
of
![]() $vK$
.
$vK$
.
Given a valuation
![]() $v$
and a coarsening
$v$
and a coarsening
![]() $w$
corresponding to the convex subgroup
$w$
corresponding to the convex subgroup
![]() $H\subseteq vK$
, we denote the induced valuation
$H\subseteq vK$
, we denote the induced valuation
![]() $\bar {v}\colon (Kw)^{\times } \to H$
on
$\bar {v}\colon (Kw)^{\times } \to H$
on
![]() $Kw$
by
$Kw$
by
![]() $\bar {v}$
, with value group
$\bar {v}$
, with value group
![]() $H$
and residue field
$H$
and residue field
![]() $Kv$
. Given a valuation
$Kv$
. Given a valuation
![]() $w$
on
$w$
on
![]() $K$
and a valuation
$K$
and a valuation
![]() $u$
on its residue field
$u$
on its residue field
![]() $Kw$
, we define the composition
$Kw$
, we define the composition
![]() $v=u\circ w$
to be the valuation with valuation ring
$v=u\circ w$
to be the valuation with valuation ring
![]() ${\mathcal {O}}_v=\operatorname {\mathrm {res}}_{w}^{-1}({\mathcal {O}}_u)$
. The valuation
${\mathcal {O}}_v=\operatorname {\mathrm {res}}_{w}^{-1}({\mathcal {O}}_u)$
. The valuation
![]() $u$
has residue field
$u$
has residue field
![]() $(Kw)u=Kv$
and value group
$(Kw)u=Kv$
and value group
![]() $u(Kw)$
, a convex subgroup of
$u(Kw)$
, a convex subgroup of
![]() $vK$
with
$vK$
with
![]() $vK/u(Kw)\cong wK$
.
$vK/u(Kw)\cong wK$
.
We can write the valuations as places and obtain the diagram:

2.3 The canonical henselian valuation
What follows is classical and can be found in greater detail in [Reference Engler and Prestel4, Section 4.4]. For any field
![]() $K$
, one can arrange henselian valuation rings on
$K$
, one can arrange henselian valuation rings on
![]() $K$
according to whether their residue field is separably closed or not. Namely, one can define
$K$
according to whether their residue field is separably closed or not. Namely, one can define
and
As above, we identify
![]() $v$
with
$v$
with
![]() $\mathcal {O}_v$
, so we will often write
$\mathcal {O}_v$
, so we will often write
![]() $v \in H_1(K)$
to mean
$v \in H_1(K)$
to mean
![]() $\mathcal {O}_v \in H_1(K)$
.
$\mathcal {O}_v \in H_1(K)$
.
The set
![]() $H_1(K)$
is linearly ordered by coarsening, with
$H_1(K)$
is linearly ordered by coarsening, with
![]() $K$
as maximum. If
$K$
as maximum. If
![]() ${H_2(K) = \varnothing }$
, then there is a finest valuation in
${H_2(K) = \varnothing }$
, then there is a finest valuation in
![]() $H_1(K)$
, which we denote by
$H_1(K)$
, which we denote by
![]() $v_K$
. Otherwise, we let
$v_K$
. Otherwise, we let
![]() $v_K$
be the coarsest valuation in
$v_K$
be the coarsest valuation in
![]() $H_2(K)$
. We call
$H_2(K)$
. We call
![]() $v_K$
the canonical henselian valuation on
$v_K$
the canonical henselian valuation on
![]() $K$
.
$K$
.

Every henselian valuation on
![]() $K$
is comparable to
$K$
is comparable to
![]() $v_K$
. Moreover,
$v_K$
. Moreover,
![]() $v_K$
is non-trivial if and only if
$v_K$
is non-trivial if and only if
![]() $K$
is henselian and not separably closed. By definition,
$K$
is henselian and not separably closed. By definition,
![]() ${Kv_K\neq (Kv_K)^{\mathrm {sep}}}$
if and only if
${Kv_K\neq (Kv_K)^{\mathrm {sep}}}$
if and only if
![]() $v_K\in H_1(K)$
if and only if
$v_K\in H_1(K)$
if and only if
![]() $H_2(K)=\varnothing $
, and if these equivalent conditions hold, then all henselian valuation rings on
$H_2(K)=\varnothing $
, and if these equivalent conditions hold, then all henselian valuation rings on
![]() $K$
are linearly ordered and coarser than
$K$
are linearly ordered and coarser than
![]() $\mathcal {O}_{v_K}$
.
$\mathcal {O}_{v_K}$
.
Remark 2.1. Let
![]() $(K,v)$
be a henselian valued field with
$(K,v)$
be a henselian valued field with
![]() $v \in H_1(K)$
. Then,
$v \in H_1(K)$
. Then,
![]() ${v_K=v_{Kv}\circ v}$
. Indeed, there is a correspondence between the set
${v_K=v_{Kv}\circ v}$
. Indeed, there is a correspondence between the set
![]() $H$
of henselian refinements of
$H$
of henselian refinements of
![]() $v$
on
$v$
on
![]() $K$
and henselian valuations on
$K$
and henselian valuations on
![]() $Kv$
. It is given by sending any refinement
$Kv$
. It is given by sending any refinement
![]() $u$
of
$u$
of
![]() $v$
to the induced valuation
$v$
to the induced valuation
![]() $\overline {u}$
on
$\overline {u}$
on
![]() $Kv$
, as in the following diagram (where valuations are written as places):
$Kv$
, as in the following diagram (where valuations are written as places):

Since the correspondence preserves residue fields,
![]() $H \cap H_1(K)$
is mapped to
$H \cap H_1(K)$
is mapped to
![]() $H_1(Kv)$
, and similarly for
$H_1(Kv)$
, and similarly for
![]() $H \cap H_2(K)$
.
$H \cap H_2(K)$
.

The correspondence preserves the coarsening relation. In particular, it follows that
![]() $v_K$
is mapped to
$v_K$
is mapped to
![]() $v_{Kv}$
and
$v_{Kv}$
and
![]() $v_K=v_{Kv}\circ v$
.
$v_K=v_{Kv}\circ v$
.
This correspondence immediately allows us to prove that condition 6 of our Main Theorem trivializes in equicharacteristic zero.
Lemma 2.2. If
![]() $Kv_K$
is henselian, then it is separably closed.
$Kv_K$
is henselian, then it is separably closed.
Proof. Suppose
![]() $Kv_K$
admits a non-trivial henselian valuation
$Kv_K$
admits a non-trivial henselian valuation
![]() $v$
. Via 2.1 this gives rise to a proper refinement of
$v$
. Via 2.1 this gives rise to a proper refinement of
![]() $v_K$
. Hence
$v_K$
. Hence
![]() $H_2(K)$
is non-empty, so
$H_2(K)$
is non-empty, so
![]() $Kv_K$
is separably closed.
$Kv_K$
is separably closed.
Corollary 2.3. Let
![]() $L\succeq Kv_K$
. Then
$L\succeq Kv_K$
. Then
![]() $(L,v_L)$
cannot have mixed characteristic.
$(L,v_L)$
cannot have mixed characteristic.
Proof. Suppose there is
![]() $L\succeq Kv_K$
such that
$L\succeq Kv_K$
such that
![]() $(L,v_L)$
has mixed characteristic. Restricting
$(L,v_L)$
has mixed characteristic. Restricting
![]() $v_L$
down to
$v_L$
down to
![]() $Kv_K$
yields a henselian valuation (because
$Kv_K$
yields a henselian valuation (because
![]() $Kv_K$
is relatively algebraically closed in
$Kv_K$
is relatively algebraically closed in
![]() $L$
) of mixed characteristic on
$L$
) of mixed characteristic on
![]() $Kv_K$
, which in particular must be non-trivial. By Lemma 2.2,
$Kv_K$
, which in particular must be non-trivial. By Lemma 2.2,
![]() $Kv_K$
must be separably closed. It follows that
$Kv_K$
must be separably closed. It follows that
![]() $L$
is also separably closed, but this implies that
$L$
is also separably closed, but this implies that
![]() $v_L$
is trivial.
$v_L$
is trivial.
2.4 Defect and tame fields
Let
![]() $(K,v) \subseteq (L,w)$
be a finite extension of a henselian valued field (note that
$(K,v) \subseteq (L,w)$
be a finite extension of a henselian valued field (note that
![]() $w$
is uniquely determined). Let
$w$
is uniquely determined). Let
![]() $p$
be the characteristic exponent of
$p$
be the characteristic exponent of
![]() $Kv$
, namely
$Kv$
, namely
![]() $p = 1$
if
$p = 1$
if
![]() $\operatorname {\mathrm {char}}(Kv) = 0$
, and
$\operatorname {\mathrm {char}}(Kv) = 0$
, and
![]() $p = \operatorname {\mathrm {char}}(Kv)$
otherwise. Then one has, by [Reference Engler and Prestel4, Theorem 3.3.3],
$p = \operatorname {\mathrm {char}}(Kv)$
otherwise. Then one has, by [Reference Engler and Prestel4, Theorem 3.3.3],
for some
![]() $d = p^\nu \in \mathbb {N}$
. We say that the extension is defectless if
$d = p^\nu \in \mathbb {N}$
. We say that the extension is defectless if
![]() $d=1$
(or equivalently
$d=1$
(or equivalently
![]() $\nu = 0$
), otherwise we say that the extension has defect (or that it is a defect extension). The valued field
$\nu = 0$
), otherwise we say that the extension has defect (or that it is a defect extension). The valued field
![]() $(K,v)$
is called defectless if all of its finite extensions are defectless. We refer to [Reference Kuhlmann15] for the details on the various equivalent definitions of “tame”.
$(K,v)$
is called defectless if all of its finite extensions are defectless. We refer to [Reference Kuhlmann15] for the details on the various equivalent definitions of “tame”.
Definition 2.4. Let
![]() $(K,v)$
be a henselian valued field and let
$(K,v)$
be a henselian valued field and let
![]() $p$
be the characteristic exponent of the residue field. Then
$p$
be the characteristic exponent of the residue field. Then
![]() $(K,v)$
is called tame if it is algebraically maximal,
$(K,v)$
is called tame if it is algebraically maximal,
![]() $vK$
is
$vK$
is
![]() $p$
-divisible, and
$p$
-divisible, and
![]() $Kv$
is perfect. Equivalently,
$Kv$
is perfect. Equivalently,
![]() $(K,v)$
is tame if it is defectless,
$(K,v)$
is tame if it is defectless,
![]() $vK$
is
$vK$
is
![]() $p$
-divisible, and
$p$
-divisible, and
![]() $Kv$
is perfect.
$Kv$
is perfect.
In the case of valued fields where
![]() $p = 1$
(i.e., valued fields of equicharacteristic zero), tame is equivalent to henselian.
$p = 1$
(i.e., valued fields of equicharacteristic zero), tame is equivalent to henselian.
Remark 2.5 (See [Reference Kuhlmann15, Section 7]).
The class of tame valued fields is an elementary class in the language
![]() $\mathcal {L}_{\mathrm {val}}$
.
$\mathcal {L}_{\mathrm {val}}$
.
2.5 t-Henselianity and saturation
A field
![]() $K$
is said to be t-henselian if it is elementarily equivalent, in
$K$
is said to be t-henselian if it is elementarily equivalent, in
![]() $\mathcal {L}_{\mathrm {ring}}$
, to a field
$\mathcal {L}_{\mathrm {ring}}$
, to a field
![]() $L$
admitting a non-trivial henselian valuation. However, a field
$L$
admitting a non-trivial henselian valuation. However, a field
![]() $K$
can be t-henselian without being henselian. The next fact is well-known, and its proof follows from [Reference Prestel and Ziegler19, Lemma 3.3] and [Reference Prestel18, p. 203].
$K$
can be t-henselian without being henselian. The next fact is well-known, and its proof follows from [Reference Prestel and Ziegler19, Lemma 3.3] and [Reference Prestel18, p. 203].
Fact 2.6. Let
![]() $K$
be t-henselian and
$K$
be t-henselian and
![]() $\aleph _1$
-saturated. Then
$\aleph _1$
-saturated. Then
![]() $K$
admits a non-trivial henselian valuation. In particular, if
$K$
admits a non-trivial henselian valuation. In particular, if
![]() $K$
is t-henselian and
$K$
is t-henselian and
![]() $K \preceq L$
is an
$K \preceq L$
is an
![]() $\aleph _1$
-saturated elementary extension, then
$\aleph _1$
-saturated elementary extension, then
![]() $L$
admits a non-trivial henselian valuation.
$L$
admits a non-trivial henselian valuation.
2.6 Definability in Jahnke–Koenigsmann
For use in later sections, we also summarize two of the main theorems of [Reference Jahnke and Koenigsmann10], which will prove to be fundamental tools in our work. In particular, we highlight how the second part of the upcoming statement allows us to often assume that the value group we are working with is divisible.
Definition 2.7. Let
![]() $p$
be a prime. An ordered abelian group
$p$
be a prime. An ordered abelian group
![]() $\Gamma $
is p-antiregular if:
$\Gamma $
is p-antiregular if:
-
(1) no non-trivial quotient of
 $\Gamma $
is
$\Gamma $
is
 $p$
-divisible,
$p$
-divisible, -
(2)
 $\Gamma $
has no rank
$\Gamma $
has no rank
 $1$
quotient.
$1$
quotient.
Theorem 2.8 [Reference Jahnke and Koenigsmann10, Theorems A and B].
Let
![]() $K$
be a henselian field which is not separably closed. Assume that
$K$
be a henselian field which is not separably closed. Assume that
![]() $K$
satisfies at least one of the following:
$K$
satisfies at least one of the following:
-
(1)
 $Kv_K$
is separably closed,
$Kv_K$
is separably closed, -
(2)
 $Kv_K$
is not t-henselian,
$Kv_K$
is not t-henselian, -
(3) there is a prime
 $p$
such that
$p$
such that
 $v_KK$
is not
$v_KK$
is not
 $p$
-divisible and not
$p$
-divisible and not
 $p$
-antiregular,
$p$
-antiregular,
then
![]() $K$
admits an
$K$
admits an
![]() $\varnothing $
-definable non-trivial henselian valuation. In general, if
$\varnothing $
-definable non-trivial henselian valuation. In general, if
![]() $v_KK$
is not divisible, then
$v_KK$
is not divisible, then
![]() $K$
admits a definable (possibly with parameters) non-trivial henselian valuation.
$K$
admits a definable (possibly with parameters) non-trivial henselian valuation.
3 Divisibility
3.1 Divisibility as an obstruction
Using classical results on elimination of quantifiers for henselian valued fields of residue characteristic zero, we know that the induced structure of the value group is that of an ordered abelian group. The proof of Theorem 1.1 crucially relies on this to obstruct the existence of definable valuations. We use the work of Jahnke and Simon in [Reference Jahnke and Simon11] to generalize this argument.
Definition 3.1. Let
![]() $\mathcal {L}_{{K,\Gamma ,k}}$
be a three-sorted language with sorts
$\mathcal {L}_{{K,\Gamma ,k}}$
be a three-sorted language with sorts
![]() $K$
(with language
$K$
(with language
![]() $\mathcal {L}_{\mathrm {ring}}$
),
$\mathcal {L}_{\mathrm {ring}}$
),
![]() $\Gamma $
(with language
$\Gamma $
(with language
![]() $\mathcal {L}_{\mathrm {oag}} \cup \{\infty \}$
), and
$\mathcal {L}_{\mathrm {oag}} \cup \{\infty \}$
), and
![]() $k$
(with language
$k$
(with language
![]() $\mathcal {L}_{\mathrm {ring}}$
), and functions
$\mathcal {L}_{\mathrm {ring}}$
), and functions
![]() $v\colon K \to \Gamma $
and
$v\colon K \to \Gamma $
and
![]() $\operatorname {res}\colon K \to k$
. Any valued field
$\operatorname {res}\colon K \to k$
. Any valued field
![]() $(K,v)$
can be interpreted as an
$(K,v)$
can be interpreted as an
![]() $\mathcal {L}_{{K,\Gamma ,k}}$
-structure in the natural way.
$\mathcal {L}_{{K,\Gamma ,k}}$
-structure in the natural way.
Fact 3.2 [Reference Jahnke and Simon11, Lemma 3.1].
Let
![]() $(K,v)$
be a tame field of positive residue characteristic. Then the value group
$(K,v)$
be a tame field of positive residue characteristic. Then the value group
![]() $vK$
is purely stably embedded as an ordered abelian group, i.e., for every
$vK$
is purely stably embedded as an ordered abelian group, i.e., for every
![]() $D \subseteq vK^n$
which is
$D \subseteq vK^n$
which is
![]() $\mathcal {L}_{{K,\Gamma ,k}}$
-definable (possibly with parameters), there is
$\mathcal {L}_{{K,\Gamma ,k}}$
-definable (possibly with parameters), there is
![]() $\psi \in \mathcal {L}_{\mathrm {oag}}(vK)$
which defines
$\psi \in \mathcal {L}_{\mathrm {oag}}(vK)$
which defines
![]() $D$
.
$D$
.
The following lemma constitutes the core of the arguments of Jahnke and Koenigsmann, and will be used repeatedly throughout our proofs as well. It relies on a classical fact about divisible ordered abelian groups, which follows from quantifier elimination.
Fact 3.3. Let
![]() $\Gamma $
be a divisible ordered abelian group. Then
$\Gamma $
be a divisible ordered abelian group. Then
![]() $\Gamma $
has no proper,
$\Gamma $
has no proper,
![]() $\mathcal {L}_{\mathrm {oag}}$
-definable (even with parameters) non-trivial convex subgroup.
$\mathcal {L}_{\mathrm {oag}}$
-definable (even with parameters) non-trivial convex subgroup.
Lemma 3.4. Suppose
![]() $(K,v)$
is a tame valued field of positive residue characteristic, with
$(K,v)$
is a tame valued field of positive residue characteristic, with
![]() $vK$
divisible. If
$vK$
divisible. If
![]() $w$
is a proper non-trivial coarsening of
$w$
is a proper non-trivial coarsening of
![]() $v$
, then
$v$
, then
![]() $w$
cannot be
$w$
cannot be
![]() $\mathcal {L}_{\mathrm {val}}$
-definable. In particular, it cannot be
$\mathcal {L}_{\mathrm {val}}$
-definable. In particular, it cannot be
![]() $\mathcal {L}_{\mathrm {ring}}$
-definable.
$\mathcal {L}_{\mathrm {ring}}$
-definable.
Proof. Suppose
![]() $w$
is
$w$
is
![]() $\mathcal {L}_{\mathrm {val}}$
-definable (possibly with parameters); then the corresponding proper non-trivial convex subgroup
$\mathcal {L}_{\mathrm {val}}$
-definable (possibly with parameters); then the corresponding proper non-trivial convex subgroup
is
![]() $\mathcal {L}_{{K,\Gamma ,k}}$
-definable (possibly with parameters) as a subset of
$\mathcal {L}_{{K,\Gamma ,k}}$
-definable (possibly with parameters) as a subset of
![]() $vK$
. By Fact 3.2,
$vK$
. By Fact 3.2,
![]() $\Delta $
is
$\Delta $
is
![]() $\mathcal {L}_{\mathrm {oag}}(vK)$
-definable. This is a contradiction, as divisible ordered abelian groups have no definable proper non-trivial convex subgroups.
$\mathcal {L}_{\mathrm {oag}}(vK)$
-definable. This is a contradiction, as divisible ordered abelian groups have no definable proper non-trivial convex subgroups.
The proof of the following theorem is then adapted directly from [Reference Jahnke and Koenigsmann10, Corollary 6.1].
Theorem 3.5. Let
![]() $(K,v_K)$
be such that
$(K,v_K)$
be such that
![]() $Kv_K$
is perfect of positive characteristic. Assume that
$Kv_K$
is perfect of positive characteristic. Assume that
![]() $K$
admits a definable non-trivial henselian valuation. Then, at least one of the following holds:
$K$
admits a definable non-trivial henselian valuation. Then, at least one of the following holds:
-
(1)
 $Kv_K$
is separably closed,
$Kv_K$
is separably closed, -
(2)
 $Kv_K$
is not t-henselian,
$Kv_K$
is not t-henselian, -
(3) there is
 $L \succeq Kv_K$
such that
$L \succeq Kv_K$
such that
 $v_LL$
is not divisible,
$v_LL$
is not divisible, -
(4)
 $v_KK$
is not divisible,
$v_KK$
is not divisible, -
(5)
 $(K,v_K)$
is not defectless,
$(K,v_K)$
is not defectless, -
(6) there is
 $L \succeq Kv_K$
such that
$L \succeq Kv_K$
such that
 $(L,v_L)$
is not defectless.
$(L,v_L)$
is not defectless.
Proof. We assume
and want to show that
![]() $K$
then cannot admit a non-trivial definable henselian valuation. Note that
$K$
then cannot admit a non-trivial definable henselian valuation. Note that
![]() $\neg 1$
means that
$\neg 1$
means that
![]() $H_2(K) = \varnothing $
. Thus, all henselian valuations on
$H_2(K) = \varnothing $
. Thus, all henselian valuations on
![]() $K$
are linearly ordered and coarser than
$K$
are linearly ordered and coarser than
![]() $v_K$
.
$v_K$
.
Now, let
![]() ${(M,v) \succeq (K,v_K)}$
be an
${(M,v) \succeq (K,v_K)}$
be an
![]() $\aleph _1$
-saturated extension in
$\aleph _1$
-saturated extension in
![]() $\mathcal {L}_{\mathrm {val}}$
. Then,
$\mathcal {L}_{\mathrm {val}}$
. Then,
![]() ${Mv \succeq Kv_K}$
is an
${Mv \succeq Kv_K}$
is an
![]() $\aleph _1$
-saturated elementary extension of a t-henselian field (by
$\aleph _1$
-saturated elementary extension of a t-henselian field (by
![]() $\neg 2$
), hence it is henselian by Fact 2.6. Since
$\neg 2$
), hence it is henselian by Fact 2.6. Since
![]() ${L := Mv\equiv Kv_K}$
is henselian and not separably closed (by
${L := Mv\equiv Kv_K}$
is henselian and not separably closed (by
![]() $\neg 1$
),
$\neg 1$
),
![]() $v_L$
is non-trivial and in fact, by Remark 2.1, we have the following diagram (where the arrows are intended as places):
$v_L$
is non-trivial and in fact, by Remark 2.1, we have the following diagram (where the arrows are intended as places):

from which we can deduce that
![]() $v_M = v_{L} \circ v$
is a proper refinement of
$v_M = v_{L} \circ v$
is a proper refinement of
![]() $v$
. Now, since
$v$
. Now, since
![]() $v_LL$
is divisible (because of
$v_LL$
is divisible (because of
![]() $\neg 3$
), so is
$\neg 3$
), so is
![]() $v_MM$
. Indeed,
$v_MM$
. Indeed,
and we know
![]() $vM$
to be divisible, as
$vM$
to be divisible, as
![]() $v_KK$
is (because of
$v_KK$
is (because of
![]() $\neg 4$
).
$\neg 4$
).
Now, by assumption
![]() $Kv_K$
is a perfect field of positive characteristic and thus so is
$Kv_K$
is a perfect field of positive characteristic and thus so is
![]() $L=Mv\succeq Kv_K$
. It follows that also the residue field
$L=Mv\succeq Kv_K$
. It follows that also the residue field
![]() $Lv_L=Mv_M$
of the valuation
$Lv_L=Mv_M$
of the valuation
![]() $v_L$
on
$v_L$
on
![]() $L$
is perfect. By assumptions
$L$
is perfect. By assumptions
![]() $\neg 5$
and
$\neg 5$
and
![]() $\neg 6$
,
$\neg 6$
,
![]() $v$
and
$v$
and
![]() $v_L$
are defectless. Thus
$v_L$
are defectless. Thus
![]() $v_M$
is defectless (as the composition of defectless valuations is defectless, see [Reference Anscombe and Jahnke2, Lemma 2.9]), and
$v_M$
is defectless (as the composition of defectless valuations is defectless, see [Reference Anscombe and Jahnke2, Lemma 2.9]), and
![]() $(M,v_M)$
is a tame valued field.
$(M,v_M)$
is a tame valued field.
Assume now that there is a non-trivial definable henselian valuation
![]() $u$
on
$u$
on
![]() $K$
, with valuation ring defined by the
$K$
, with valuation ring defined by the
![]() $\mathcal {L}_{\mathrm {ring}}(K)$
-formula
$\mathcal {L}_{\mathrm {ring}}(K)$
-formula
![]() $\psi (x)$
. Because of
$\psi (x)$
. Because of
![]() $\neg 1$
,
$\neg 1$
,
![]() $u$
is a (not necessarily proper) coarsening of
$u$
is a (not necessarily proper) coarsening of
![]() $v_K$
. Now, via the elementary embedding,
$v_K$
. Now, via the elementary embedding,
![]() $\psi (x)$
defines a valuation
$\psi (x)$
defines a valuation
![]() $u^*$
on
$u^*$
on
![]() $M$
, which is a coarsening of
$M$
, which is a coarsening of
![]() $v$
and hence a proper coarsening of
$v$
and hence a proper coarsening of
![]() $v_M$
. This is a contradiction to Lemma 3.4.
$v_M$
. This is a contradiction to Lemma 3.4.
3.2 Failure of divisibility as a source of definability
We now seek to extend the arguments given in [Reference Jahnke and Koenigsmann10, Proposition 5.5] of the case when
![]() $v_KK$
is itself divisible, but there is an elementary extension
$v_KK$
is itself divisible, but there is an elementary extension
![]() $L$
of
$L$
of
![]() $Kv_K$
which is henselian with non-divisible value group
$Kv_K$
which is henselian with non-divisible value group
![]() $v_LL$
.
$v_LL$
.
Proposition 3.6. Let
![]() $K$
be a henselian field, and let
$K$
be a henselian field, and let
![]() $v_K$
be its canonical henselian valuation. If:
$v_K$
be its canonical henselian valuation. If:
-
(1) there is
 $L\equiv Kv_K$
such that
$L\equiv Kv_K$
such that
 $v_L L$
is non-divisible, and
$v_L L$
is non-divisible, and -
(2)
 $v_K K$
is divisible,
$v_K K$
is divisible,
then
![]() $K$
admits an
$K$
admits an
![]() $\varnothing $
-definable non-trivial henselian valuation.
$\varnothing $
-definable non-trivial henselian valuation.
Proof. Let
![]() $L\equiv Kv_K$
be such that
$L\equiv Kv_K$
be such that
![]() $v_L L$
is non-divisible. First, we notice that
$v_L L$
is non-divisible. First, we notice that
![]() $Kv_K$
is not separably closed, and hence by Lemma 2.2 it does not admit any non-trivial henselian valuation. Indeed, if
$Kv_K$
is not separably closed, and hence by Lemma 2.2 it does not admit any non-trivial henselian valuation. Indeed, if
![]() $Kv_K$
were separably closed,
$Kv_K$
were separably closed,
![]() $L$
would also be separably closed, but separably closed valued fields always have divisible value group, and
$L$
would also be separably closed, but separably closed valued fields always have divisible value group, and
![]() $v_LL$
is not divisible by assumption.
$v_LL$
is not divisible by assumption.
We now claim that
![]() $v_L \in H_1(L)$
. Assume for a contradiction that it is not. Then by Theorem 2.8, there is an
$v_L \in H_1(L)$
. Assume for a contradiction that it is not. Then by Theorem 2.8, there is an
![]() $\varnothing $
-definable non-trivial henselian valuation on
$\varnothing $
-definable non-trivial henselian valuation on
![]() $L$
. Thus there is also an
$L$
. Thus there is also an
![]() $\varnothing $
-definable non-trivial henselian valuation
$\varnothing $
-definable non-trivial henselian valuation
![]() $u$
on
$u$
on
![]() $Kv_K$
by elementary equivalence, contradicting the considerations in the previous paragraph.
$Kv_K$
by elementary equivalence, contradicting the considerations in the previous paragraph.
By the Keisler–Shelah isomorphism theorem [Reference Marker17, Theorem 2.5.36], there are an index set
![]() $I$
and an ultrafilter
$I$
and an ultrafilter
![]() $\mathcal U$
on
$\mathcal U$
on
![]() $I$
such that
$I$
such that
![]() $L^{\mathcal U} \cong (Kv_K)^{\mathcal U}$
. Take the ultrapower
$L^{\mathcal U} \cong (Kv_K)^{\mathcal U}$
. Take the ultrapower
![]() $(L^{\mathcal U}, v_L^{\mathcal U}) := (L,v_L)^{\mathcal U}$
as an
$(L^{\mathcal U}, v_L^{\mathcal U}) := (L,v_L)^{\mathcal U}$
as an
![]() $\mathcal {L}_{\mathrm {val}}$
-structure. Then,
$\mathcal {L}_{\mathrm {val}}$
-structure. Then,
![]() $v_L^{\mathcal U}L^{\mathcal U} \equiv v_LL$
is not divisible. Since
$v_L^{\mathcal U}L^{\mathcal U} \equiv v_LL$
is not divisible. Since
![]() $v_L \in H_1(L)$
, then
$v_L \in H_1(L)$
, then
![]() $v_L^{\mathcal U} \in H_1(L^{\mathcal U})$
and thus
$v_L^{\mathcal U} \in H_1(L^{\mathcal U})$
and thus
![]() $v_L^{\mathcal U}$
coarsens the canonical henselian valuation
$v_L^{\mathcal U}$
coarsens the canonical henselian valuation
![]() $v_{L^{\mathcal U}}$
on
$v_{L^{\mathcal U}}$
on
![]() $L^{\mathcal U}$
. In particular, also
$L^{\mathcal U}$
. In particular, also
![]() $v_{L^{\mathcal U}}L^{\mathcal U}$
cannot be divisible, say not
$v_{L^{\mathcal U}}L^{\mathcal U}$
cannot be divisible, say not
![]() $q$
-divisible for some prime
$q$
-divisible for some prime
![]() $q$
. Moreover, if we let
$q$
. Moreover, if we let
![]() $(K^{\mathcal U}, v_K^{\mathcal U}) := (K,v_K)^{\mathcal U}$
as an
$(K^{\mathcal U}, v_K^{\mathcal U}) := (K,v_K)^{\mathcal U}$
as an
![]() $\mathcal {L}_{\mathrm {val}}$
-structure, then
$\mathcal {L}_{\mathrm {val}}$
-structure, then
![]() $K^{\mathcal U}v_K^{\mathcal U} = L^{\mathcal U}$
and
$K^{\mathcal U}v_K^{\mathcal U} = L^{\mathcal U}$
and
![]() $v_K^{\mathcal U}K^{\mathcal U} \equiv v_KK$
is divisible. Now:
$v_K^{\mathcal U}K^{\mathcal U} \equiv v_KK$
is divisible. Now:
-
•
 $K^{\mathcal U}$
is henselian and
$K^{\mathcal U}$
is henselian and
 $v_{K^{\mathcal U}} = v_{L^{\mathcal U}}\circ v_K^{\mathcal U} $
(Remark 2.1),
$v_{K^{\mathcal U}} = v_{L^{\mathcal U}}\circ v_K^{\mathcal U} $
(Remark 2.1), -
•
 $v_{L^{\mathcal U}}L^{\mathcal U} \subseteq v_{K^{\mathcal U}}K^{\mathcal U}$
is a convex subgroup and thus also
$v_{L^{\mathcal U}}L^{\mathcal U} \subseteq v_{K^{\mathcal U}}K^{\mathcal U}$
is a convex subgroup and thus also
 $v_{K^{\mathcal U}}K^{\mathcal U}$
is not
$v_{K^{\mathcal U}}K^{\mathcal U}$
is not
 $q$
-divisible, and
$q$
-divisible, and -
•
 $v_{K^{\mathcal U}}K^{\mathcal U}/v_{L^{\mathcal U}}L^{\mathcal U} \cong v_K^{\mathcal U} K^{\mathcal U}$
is divisible, hence
$v_{K^{\mathcal U}}K^{\mathcal U}/v_{L^{\mathcal U}}L^{\mathcal U} \cong v_K^{\mathcal U} K^{\mathcal U}$
is divisible, hence
 $v_{K^{\mathcal U}}K^{\mathcal U}$
is not
$v_{K^{\mathcal U}}K^{\mathcal U}$
is not
 $q$
-antiregular.
$q$
-antiregular.
We can then apply Theorem 2.8 to
![]() $(K^{\mathcal U}, v_{K^{\mathcal U}})$
(note the different valuation!) and find an
$(K^{\mathcal U}, v_{K^{\mathcal U}})$
(note the different valuation!) and find an
![]() $\varnothing $
-definable non-trivial henselian valuation on
$\varnothing $
-definable non-trivial henselian valuation on
![]() $K^{\mathcal U}$
. Since
$K^{\mathcal U}$
. Since
![]() ${K \preceq K^{\mathcal U}}$
, the same
${K \preceq K^{\mathcal U}}$
, the same
![]() $\mathcal {L}_{\mathrm {ring}}$
-formula defines a non-trivial henselian valuation ring on
$\mathcal {L}_{\mathrm {ring}}$
-formula defines a non-trivial henselian valuation ring on
![]() $K$
.
$K$
.
4 Defect
Defect—i.e., the quantity
![]() $d$
in equation (⋆)—measures how much of the finite extension of a henselian valued field
$d$
in equation (⋆)—measures how much of the finite extension of a henselian valued field
![]() $(K,v)$
is not induced by extensions of its value group
$(K,v)$
is not induced by extensions of its value group
![]() $vK$
and residue field
$vK$
and residue field
![]() $Kv$
. Originally introduced by Ostrowski (see [Reference Roquette21] for a thorough summary of his work), it was then extensively studied by Franz-Viktor Kuhlmann in his thesis [Reference Kuhlmann14] and his subsequent work. While in classical number theoretic situations, defect is trivial, it is a crucial invariant in the model theory of valued fields, in a certain sense limiting the Ax-Kochen/Ershov philosophy. In residue characteristic zero, every extension is defectless; this is why, for example, the classical Ax-Kochen/Ershov theorem can be proven for all henselian equicharacteristic zero valued fields.
$Kv$
. Originally introduced by Ostrowski (see [Reference Roquette21] for a thorough summary of his work), it was then extensively studied by Franz-Viktor Kuhlmann in his thesis [Reference Kuhlmann14] and his subsequent work. While in classical number theoretic situations, defect is trivial, it is a crucial invariant in the model theory of valued fields, in a certain sense limiting the Ax-Kochen/Ershov philosophy. In residue characteristic zero, every extension is defectless; this is why, for example, the classical Ax-Kochen/Ershov theorem can be proven for all henselian equicharacteristic zero valued fields.
Valued fields of positive residue characteristic showcase wildly different behaviour. In particular, the fundamental equality can fail, i.e., there might be an extension with
![]() $d> 1$
. This is usually a serious obstruction to most efforts in understanding complete theories of valued fields. Throughout this section, however, we will deploy such extensions to define henselian valuations.
$d> 1$
. This is usually a serious obstruction to most efforts in understanding complete theories of valued fields. Throughout this section, however, we will deploy such extensions to define henselian valuations.
4.1 A toy situation
Suppose that
![]() $v \in H_1(K)$
and there exists an
$v \in H_1(K)$
and there exists an
![]() $\mathcal {L}_{\mathrm {ring}}$
-definable subset
$\mathcal {L}_{\mathrm {ring}}$
-definable subset
![]() $D$
of
$D$
of
![]() $K$
with
$K$
with
where
![]() $H$
is a proper convex subgroup of
$H$
is a proper convex subgroup of
![]() $vK$
.
$vK$
.

We will prove that whenever
![]() $(K,v)$
is as above, then there is a definable coarsening of
$(K,v)$
is as above, then there is a definable coarsening of
![]() $v$
which corresponds to
$v$
which corresponds to
![]() $H$
, see Section 2.2. This is a simplified version of the situation that will show up later when working with independent defect extensions. All the main ideas are already contained in this proof, with the advantage that we can avoid the technical subtleties of working modulo an interpretation of a finite field extension, which make the proof of Theorem 4.11 cumbersome.
$H$
, see Section 2.2. This is a simplified version of the situation that will show up later when working with independent defect extensions. All the main ideas are already contained in this proof, with the advantage that we can avoid the technical subtleties of working modulo an interpretation of a finite field extension, which make the proof of Theorem 4.11 cumbersome.
Remark 4.1. We will repeatedly use Beth’s definability theorem [Reference Hodges7, Theorem 5.5.4]. In our case, this means that in order to show that a certain subset
![]() $D \subseteq K^n$
is
$D \subseteq K^n$
is
![]() $\mathcal {L}_{\mathrm {ring}}(\overline {c})$
-definable on
$\mathcal {L}_{\mathrm {ring}}(\overline {c})$
-definable on
![]() $K$
, where
$K$
, where
![]() $\overline {c}$
are some candidate parameters, it is enough to work in the augmented language
$\overline {c}$
are some candidate parameters, it is enough to work in the augmented language
![]() ${\mathcal {L} = \mathcal {L}_{\mathrm {ring}}(\overline {c}) \cup \{P(X_1, \dots ,X_n)\}}$
, and show that whenever we take two structures
${\mathcal {L} = \mathcal {L}_{\mathrm {ring}}(\overline {c}) \cup \{P(X_1, \dots ,X_n)\}}$
, and show that whenever we take two structures
![]() ${(L,\overline {c}^{\prime },D_1), (L,\overline {c}^{\prime },D_2) \equiv _{\mathcal {L}} (K,\overline {c},D)}$
, we have
${(L,\overline {c}^{\prime },D_1), (L,\overline {c}^{\prime },D_2) \equiv _{\mathcal {L}} (K,\overline {c},D)}$
, we have
![]() $D_1 = D_2$
. In particular, in the proof of Lemma 4.2, we will consider valuation rings and thus unary predicates.
$D_1 = D_2$
. In particular, in the proof of Lemma 4.2, we will consider valuation rings and thus unary predicates.
Lemma 4.2. Let
![]() $(K,v)$
be a valued field such that
$(K,v)$
be a valued field such that
![]() $v \in H_1(K)$
. Let
$v \in H_1(K)$
. Let
![]() $D \subseteq K$
be an
$D \subseteq K$
be an
![]() $\mathcal {L}_{\mathrm {ring}}$
-definable subset such that, for some proper convex subgroup
$\mathcal {L}_{\mathrm {ring}}$
-definable subset such that, for some proper convex subgroup
![]() $H \subseteq vK$
(possibly equal to the trivial subgroup),
$H \subseteq vK$
(possibly equal to the trivial subgroup),
Let
![]() $v_H$
be the coarsening of
$v_H$
be the coarsening of
![]() $v$
corresponding to
$v$
corresponding to
![]() $H$
and denote by
$H$
and denote by
![]() $\mathcal {O}_H$
its valuation ring. Then
$\mathcal {O}_H$
its valuation ring. Then
![]() $v_H$
is definable.
$v_H$
is definable.
Proof. We will use Beth’s definability theorem as explained in Remark 4.1. We work in
![]() $\mathcal {L}_{\mathrm {val}}$
: let
$\mathcal {L}_{\mathrm {val}}$
: let
![]() $L$
and
$L$
and
![]() $\mathcal {O}_1, \mathcal {O}_2 \subseteq L$
be such that
$\mathcal {O}_1, \mathcal {O}_2 \subseteq L$
be such that
![]() ${(L,\mathcal {O}_1), (L,\mathcal {O}_2) \equiv (K,\mathcal {O}_H)}$
. In particular, both
${(L,\mathcal {O}_1), (L,\mathcal {O}_2) \equiv (K,\mathcal {O}_H)}$
. In particular, both
![]() $\mathcal {O}_1$
and
$\mathcal {O}_1$
and
![]() $\mathcal {O}_2$
are henselian valuation rings on
$\mathcal {O}_2$
are henselian valuation rings on
![]() $L$
, corresponding to valuations
$L$
, corresponding to valuations
![]() $v_1$
and
$v_1$
and
![]() $v_2$
. We want to show that
$v_2$
. We want to show that
![]() $\mathcal {O}_1 = \mathcal {O}_2$
. Note that, since
$\mathcal {O}_1 = \mathcal {O}_2$
. Note that, since
![]() $v_H \in H_1(K)$
, the same holds for
$v_H \in H_1(K)$
, the same holds for
![]() $v_1$
and
$v_1$
and
![]() $v_2$
, and thus
$v_2$
, and thus
![]() $\mathcal {O}_1$
and
$\mathcal {O}_1$
and
![]() $\mathcal {O}_2$
are comparable. Without loss of generality, assume
$\mathcal {O}_2$
are comparable. Without loss of generality, assume
![]() $\mathcal {O}_1 \subseteq \mathcal {O}_2$
. This implies that
$\mathcal {O}_1 \subseteq \mathcal {O}_2$
. This implies that
![]() $\mathcal {O}_1^\times \subseteq \mathcal {O}_2^\times $
. We note that, if
$\mathcal {O}_1^\times \subseteq \mathcal {O}_2^\times $
. We note that, if
![]() $D = \psi (K)$
for some
$D = \psi (K)$
for some
![]() $\mathcal {L}_{\mathrm {ring}}$
-formula
$\mathcal {L}_{\mathrm {ring}}$
-formula
![]() $\psi $
(possibly with parameters), then
$\psi $
(possibly with parameters), then
 $$\begin{align*}(K,\mathcal{O}_H) \vDash \forall x \left(x \notin \mathcal{O}_H \iff \exists u \exists y \left(u \in \mathcal{O}_H^\times \land \psi(y) \land \left(x = u\frac{1}{y}\right)\right)\right). \end{align*}$$
$$\begin{align*}(K,\mathcal{O}_H) \vDash \forall x \left(x \notin \mathcal{O}_H \iff \exists u \exists y \left(u \in \mathcal{O}_H^\times \land \psi(y) \land \left(x = u\frac{1}{y}\right)\right)\right). \end{align*}$$
The same
![]() $\mathcal {L}_{\mathrm {val}}$
-sentence is then true in both
$\mathcal {L}_{\mathrm {val}}$
-sentence is then true in both
![]() $(L,\mathcal {O}_1)$
and
$(L,\mathcal {O}_1)$
and
![]() $(L,\mathcal {O}_2)$
.
$(L,\mathcal {O}_2)$
.
Now, towards proving
![]() $\mathcal {O}_1 = \mathcal {O}_2$
, assume for a contradiction that there is
$\mathcal {O}_1 = \mathcal {O}_2$
, assume for a contradiction that there is
![]() $x \in \mathcal {O}_2$
but
$x \in \mathcal {O}_2$
but
![]() $x \notin \mathcal {O}_1$
: then, there exist
$x \notin \mathcal {O}_1$
: then, there exist
![]() $u \in \mathcal {O}_1^\times \subseteq \mathcal {O}_2^\times $
and
$u \in \mathcal {O}_1^\times \subseteq \mathcal {O}_2^\times $
and
![]() $d \in \psi (L)$
such that
$d \in \psi (L)$
such that
![]() $x = u\frac {1}{d}$
. In particular, then, by the
$x = u\frac {1}{d}$
. In particular, then, by the
![]() $\mathcal {L}_{\mathrm {val}}$
-sentence above,
$\mathcal {L}_{\mathrm {val}}$
-sentence above,
![]() $x \notin \mathcal {O}_2$
, a contradiction. It follows that
$x \notin \mathcal {O}_2$
, a contradiction. It follows that
![]() $\mathcal {O}_1 = \mathcal {O}_2$
.
$\mathcal {O}_1 = \mathcal {O}_2$
.
We can apply Beth’s definability theorem and get that
![]() $\mathcal {O}_H = \varphi (K)$
for some
$\mathcal {O}_H = \varphi (K)$
for some
![]() $\mathcal {L}_{\mathrm {ring}}$
-formula
$\mathcal {L}_{\mathrm {ring}}$
-formula
![]() $\varphi (x)$
.
$\varphi (x)$
.
Remark 4.3. Beth’s definability theorem grants some control over parameters; namely, if
![]() $D$
was
$D$
was
![]() $\varnothing $
-definable to begin with, then so is
$\varnothing $
-definable to begin with, then so is
![]() $\mathcal {O}_H$
. Moreover, the same argument works if we replace
$\mathcal {O}_H$
. Moreover, the same argument works if we replace
![]() $\mathcal {L}_{\mathrm {ring}}$
with some expansion
$\mathcal {L}_{\mathrm {ring}}$
with some expansion
![]() $\mathcal {L}$
; we then get that
$\mathcal {L}$
; we then get that
![]() $v_H$
is
$v_H$
is
![]() $\mathcal {L}$
-definable.
$\mathcal {L}$
-definable.
4.2 Independent defect
Independent defect will be the central tool of our definability proof; the set
![]() $\Sigma _L$
which will be defined in a moment, while not
$\Sigma _L$
which will be defined in a moment, while not
![]() $\mathcal {L}_{\mathrm {ring}}$
-definable per se, will contain enough information to
$\mathcal {L}_{\mathrm {ring}}$
-definable per se, will contain enough information to
![]() $\mathcal {L}_{\mathrm {ring}}$
-define a henselian valuation ring modulo the interpretation of a finite field extension.
$\mathcal {L}_{\mathrm {ring}}$
-define a henselian valuation ring modulo the interpretation of a finite field extension.
Note that every equicharacteristic
![]() $0$
valued field is defectless, so for the rest of this section we assume that our valued fields have residue characteristic
$0$
valued field is defectless, so for the rest of this section we assume that our valued fields have residue characteristic
![]() $p>0$
.
$p>0$
.
Definition 4.4 [Reference Kuhlmann and Rzepka16, Introduction].
Let
![]() $(K,v) \subseteq (L,v)$
be a Galois extension of degree
$(K,v) \subseteq (L,v)$
be a Galois extension of degree
![]() $p$
with defect. For any
$p$
with defect. For any
![]() $\sigma \in {\operatorname {Gal}(L | K)} \setminus \{\mathrm {id}\}$
, we let
$\sigma \in {\operatorname {Gal}(L | K)} \setminus \{\mathrm {id}\}$
, we let

Fact 4.5 [Reference Kuhlmann and Rzepka16, Theorems 3.4 and 3.5].
![]() $\Sigma _\sigma $
does not depend on the choice of
$\Sigma _\sigma $
does not depend on the choice of
![]() $\sigma $
, and is a final segment of
$\sigma $
, and is a final segment of
![]() ${vK}_{\infty }$
. We denote it by
${vK}_{\infty }$
. We denote it by
![]() $\Sigma _L$
.
$\Sigma _L$
.
Definition 4.6 [Reference Kuhlmann and Rzepka16, Introduction].
The extension
![]() $(K,v) \subseteq (L,v)$
has independent defect if there is a (possibly trivial) proper convex subgroup
$(K,v) \subseteq (L,v)$
has independent defect if there is a (possibly trivial) proper convex subgroup
![]() $H \subseteq vK$
such that
$H \subseteq vK$
such that
![]() $vK/H$
does not have a minimum positive element, and further
$vK/H$
does not have a minimum positive element, and further
We say that the extension has dependent defect otherwise.
Definition 4.7 [Reference Kuhlmann and Rzepka16, Introduction].
Let
![]() $(K,v)$
be a henselian valued field of positive residue characteristic
$(K,v)$
be a henselian valued field of positive residue characteristic
![]() $p$
. If
$p$
. If
![]() $\operatorname {\mathrm {char}}(K)=0$
, then let
$\operatorname {\mathrm {char}}(K)=0$
, then let ![]() where
where
![]() $\zeta _p$
is a primitive
$\zeta _p$
is a primitive
![]() $p$
th root of unity. Otherwise let
$p$
th root of unity. Otherwise let ![]() . We denote the unique extension of
. We denote the unique extension of
![]() $v$
to
$v$
to
![]() $K'$
also by
$K'$
also by
![]() $v$
. We say that
$v$
. We say that
![]() $(K,v)$
is an independent defect field if all Galois defect extensions of
$(K,v)$
is an independent defect field if all Galois defect extensions of
![]() $(K',v)$
of degree
$(K',v)$
of degree
![]() $p$
have independent defect.
$p$
have independent defect.
We now prove a result on composition of independent defect valuations with defectless valuations, which will be quite useful later.
Lemma 4.8. Let
![]() $(K,v)$
be a henselian valued field with
$(K,v)$
be a henselian valued field with
![]() $v=\bar {v}\circ w$
, such that
$v=\bar {v}\circ w$
, such that
![]() $(K,w)$
is defectless and
$(K,w)$
is defectless and
![]() $(Kw,\bar {v})$
is a perfect independent defect field. Then
$(Kw,\bar {v})$
is a perfect independent defect field. Then
![]() $(K,v)$
is an independent defect field.
$(K,v)$
is an independent defect field.
Proof. Assume that
![]() $v = \bar {v} \circ w$
, with
$v = \bar {v} \circ w$
, with
![]() $w$
defectless and
$w$
defectless and
![]() $(Kw, \bar {v})$
a perfect independent defect field. If
$(Kw, \bar {v})$
a perfect independent defect field. If
![]() $(K,v)$
has mixed characteristic
$(K,v)$
has mixed characteristic
![]() $(0,p)$
we assume without loss of generality that
$(0,p)$
we assume without loss of generality that
![]() $K$
contains a primitive
$K$
contains a primitive
![]() $p$
th root of unity.
$p$
th root of unity.

Let
![]() $(L,v)$
be a Galois defect extension of degree
$(L,v)$
be a Galois defect extension of degree
![]() $p$
of
$p$
of
![]() $(K,v)$
. In particular, this extension is immediate, i.e.,
$(K,v)$
. In particular, this extension is immediate, i.e.,
![]() $Lv=Kv$
and
$Lv=Kv$
and
![]() $vL=vK$
. We want to show that
$vL=vK$
. We want to show that
![]() $(L,v)\supseteq (K,v)$
has independent defect.
$(L,v)\supseteq (K,v)$
has independent defect.
We first argue that
![]() $(Kw,\bar {v}) \subseteq (Lw,\bar {v})$
is a defect extension. We prove that it is immediate of degree
$(Kw,\bar {v}) \subseteq (Lw,\bar {v})$
is a defect extension. We prove that it is immediate of degree
![]() $p$
. As
$p$
. As
![]() $(K,w)$
is defectless, we have the fundamental equality
$(K,w)$
is defectless, we have the fundamental equality
We argue that we must have
![]() $[Lw:Kw] = p$
and
$[Lw:Kw] = p$
and
![]() $wL = wK$
. Suppose not, i.e., that
$wL = wK$
. Suppose not, i.e., that
![]() $Lw=Kw$
: then
$Lw=Kw$
: then
![]() $\bar {v}(Lw)=\bar {v}(Kw)$
, and thus
$\bar {v}(Lw)=\bar {v}(Kw)$
, and thus
contradicting
![]() $(wL:wK)=p$
.
$(wL:wK)=p$
.
Using
![]() $wL = wK$
and
$wL = wK$
and
![]() $vL=vK$
, we get
$vL=vK$
, we get
and thus
![]() $\bar {v}(Lw)=\bar {v}(Kw)$
. Moreover,
$\bar {v}(Lw)=\bar {v}(Kw)$
. Moreover,
![]() $(Lw)\bar {v}=Lv=Kv=(Kw)\bar {v}$
. This shows that
$(Lw)\bar {v}=Lv=Kv=(Kw)\bar {v}$
. This shows that
![]() $ (Kw,\bar {v}) \subseteq (Lw,\bar {v}) $
is an immediate extension of degree
$ (Kw,\bar {v}) \subseteq (Lw,\bar {v}) $
is an immediate extension of degree
![]() $p$
, in particular a defect extension. Note that as
$p$
, in particular a defect extension. Note that as
![]() $Kw$
is perfect, the extension is separable; moreover, since
$Kw$
is perfect, the extension is separable; moreover, since
![]() $K \subseteq L$
is normal, the same holds for
$K \subseteq L$
is normal, the same holds for
![]() $Kw \subseteq Lw$
(for example, by [Reference Engler and Prestel4, Proposition 3.2.16]), and thus the latter is Galois. Since
$Kw \subseteq Lw$
(for example, by [Reference Engler and Prestel4, Proposition 3.2.16]), and thus the latter is Galois. Since
![]() $(Kw,\bar {v})$
is an independent defect field, the extension
$(Kw,\bar {v})$
is an independent defect field, the extension
![]() $ (Kw,\bar {v}) \subseteq (Lw,\bar {v}) $
has independent defect. By definition, there is a convex subgroup
$ (Kw,\bar {v}) \subseteq (Lw,\bar {v}) $
has independent defect. By definition, there is a convex subgroup
![]() $H$
of
$H$
of
![]() $\bar {v}(Kw)$
such that
$\bar {v}(Kw)$
such that ![]() has no minimum positive element, and further
has no minimum positive element, and further

where
![]() $\tau \in {\operatorname {Gal}({Lw} | {Kw})}$
is a generator, i.e.,
$\tau \in {\operatorname {Gal}({Lw} | {Kw})}$
is a generator, i.e.,
![]() ${\langle \tau \rangle ={\operatorname {Gal}({Lw} | {Kw})}}$
. Since
${\langle \tau \rangle ={\operatorname {Gal}({Lw} | {Kw})}}$
. Since
![]() $\bar {v}(Kw)\subseteq vK$
is a convex subgroup,
$\bar {v}(Kw)\subseteq vK$
is a convex subgroup,
![]() $H$
is also a convex subgroup of the bigger group
$H$
is also a convex subgroup of the bigger group
![]() $vK$
. Then, the embedding
$vK$
. Then, the embedding
![]() $\bar {v}(Kw) \subseteq vK$
gives rise to an embedding
$\bar {v}(Kw) \subseteq vK$
gives rise to an embedding ![]() as convex subgroup, thus
as convex subgroup, thus ![]() also has no minimum positive element. We will now show that
also has no minimum positive element. We will now show that

where
![]() $\sigma \in {\operatorname {Gal}({L} | {K})}$
is such that
$\sigma \in {\operatorname {Gal}({L} | {K})}$
is such that
![]() $\langle \sigma \rangle ={\operatorname {Gal}({L} | {K})}$
. This will prove that the defect in the extension
$\langle \sigma \rangle ={\operatorname {Gal}({L} | {K})}$
. This will prove that the defect in the extension
![]() $(L,v)\supseteq (K,v)$
is independent.
$(L,v)\supseteq (K,v)$
is independent.
As
![]() $\Sigma _L$
is a final segment in
$\Sigma _L$
is a final segment in
![]() ${vK}_{\infty }$
(by Fact 4.5), it is enough to show that
${vK}_{\infty }$
(by Fact 4.5), it is enough to show that
![]() $\Sigma _{L}\cap {\bar {v}(Kw)}_{\infty } = \Sigma _{Lw}$
.
$\Sigma _{L}\cap {\bar {v}(Kw)}_{\infty } = \Sigma _{Lw}$
.
Note that since
![]() $(K,w)$
is henselian,
$(K,w)$
is henselian,
![]() $\mathcal {O}_{(L,w)}$
is fixed setwise by the action of
$\mathcal {O}_{(L,w)}$
is fixed setwise by the action of
![]() ${\operatorname {Gal}({L} | {K})}$
. Thus by [Reference Engler and Prestel4, Proposition 3.2.16(3)],
${\operatorname {Gal}({L} | {K})}$
. Thus by [Reference Engler and Prestel4, Proposition 3.2.16(3)],
![]() $\phi $
induces an automorphism
$\phi $
induces an automorphism
![]() $\bar {\phi }\in {\operatorname {Gal}({Lw} | {Kw})}$
given by
$\bar {\phi }\in {\operatorname {Gal}({Lw} | {Kw})}$
given by
We argue that the map
 $$\begin{align*}\left\lbrace \begin{array}{rcl} {\operatorname{Gal}({L} | {K})} &\to&{\operatorname{Gal}({Lw} | {Kw})}\\ \phi&\mapsto &\bar{\phi} \end{array}\right. \end{align*}$$
$$\begin{align*}\left\lbrace \begin{array}{rcl} {\operatorname{Gal}({L} | {K})} &\to&{\operatorname{Gal}({Lw} | {Kw})}\\ \phi&\mapsto &\bar{\phi} \end{array}\right. \end{align*}$$
is a surjective group homomorphism (cf. the proof of [Reference Engler and Prestel4, Lemma 5.2.6]): indeed, we write
![]() $Lw = Kw(\operatorname {\mathrm {res}}_w(a))$
, and we take any
$Lw = Kw(\operatorname {\mathrm {res}}_w(a))$
, and we take any
![]() $\rho \in {\operatorname {Gal}({Lw} | {Kw})}$
. We let
$\rho \in {\operatorname {Gal}({Lw} | {Kw})}$
. We let
![]() $a_1, \dots , a_p$
be the
$a_1, \dots , a_p$
be the
![]() ${\operatorname {Gal}({L} | {K})}$
-conjugates of
${\operatorname {Gal}({L} | {K})}$
-conjugates of
![]() $a$
.
$a$
.
For some
![]() $i \leq p$
,
$i \leq p$
,
![]() ${\operatorname {\mathrm {res}}_w(a_i) = \rho (\operatorname {\mathrm {res}}_w(a))}$
, so there is
${\operatorname {\mathrm {res}}_w(a_i) = \rho (\operatorname {\mathrm {res}}_w(a))}$
, so there is
![]() $\sigma \in {\operatorname {Gal}({L} | {K})}$
such that
$\sigma \in {\operatorname {Gal}({L} | {K})}$
such that
Thus
![]() $\bar {\sigma }$
and
$\bar {\sigma }$
and
![]() $\rho $
coincide on
$\rho $
coincide on
![]() $Lw$
.
$Lw$
.
Now, since
![]() $(\phi \mapsto \bar {\phi })$
is surjective between finite groups with the same order, it is an isomorphism. It follows that it maps generators of
$(\phi \mapsto \bar {\phi })$
is surjective between finite groups with the same order, it is an isomorphism. It follows that it maps generators of
![]() ${\operatorname {Gal}({L} | {K})}$
to generators of
${\operatorname {Gal}({L} | {K})}$
to generators of
![]() ${\operatorname {Gal}({Lw} | {Kw})}$
.
${\operatorname {Gal}({Lw} | {Kw})}$
.
We can now compare the sets
![]() $\Sigma _L$
and
$\Sigma _L$
and
![]() $\Sigma _{Lw}$
.
$\Sigma _{Lw}$
.
Step 1:
![]() $\Sigma _{Lw}\subseteq \Sigma _{L}\cap {\bar {v}(Kw)}_{\infty }$
.
$\Sigma _{Lw}\subseteq \Sigma _{L}\cap {\bar {v}(Kw)}_{\infty }$
.
Fix
![]() $\sigma \in {\operatorname {Gal}({L} | {K})}$
such that
$\sigma \in {\operatorname {Gal}({L} | {K})}$
such that
![]() $\langle \sigma \rangle ={\operatorname {Gal}({L} | {K})}$
. Then, since the set
$\langle \sigma \rangle ={\operatorname {Gal}({L} | {K})}$
. Then, since the set
![]() $\Sigma _{Lw}$
does not depend on the choice of the generator, we can write
$\Sigma _{Lw}$
does not depend on the choice of the generator, we can write
 $$ \begin{align*} \Sigma_{Lw}&=\left\{ \bar{v}\left( \frac{f-\bar{\sigma}(f)}{f} \right) \mathrel{\Big|} f\in(Lw)^\times \right\}\\ &=\left\{ \bar{v}\left( \frac{\operatorname{\mathrm{res}}_w(f)-\bar{\sigma}(\operatorname{\mathrm{res}}_w(f))}{\operatorname{\mathrm{res}}_w(f)} \right) \mathrel{\Big|} f\in \mathcal{O}_{(L,w)}^\times \right\}\\ &=\left\{ \bar{v}\left(\operatorname{\mathrm{res}}_w\left( \frac{f-\sigma(f)}{f} \right)\right) \mathrel{\Big|} f\in \mathcal{O}_{(L,w)}^\times \right\}\\ &= \left\{ v\left( \frac{f-\sigma(f)}{f} \right) \mathrel{\Big|} f\in \mathcal{O}_{(L,w)}^\times \right\}\cap {\bar{v}(Kw)}_{\infty} \subseteq\Sigma_{L}\cap {\bar{v}(Kw)}_{\infty}, \end{align*} $$
$$ \begin{align*} \Sigma_{Lw}&=\left\{ \bar{v}\left( \frac{f-\bar{\sigma}(f)}{f} \right) \mathrel{\Big|} f\in(Lw)^\times \right\}\\ &=\left\{ \bar{v}\left( \frac{\operatorname{\mathrm{res}}_w(f)-\bar{\sigma}(\operatorname{\mathrm{res}}_w(f))}{\operatorname{\mathrm{res}}_w(f)} \right) \mathrel{\Big|} f\in \mathcal{O}_{(L,w)}^\times \right\}\\ &=\left\{ \bar{v}\left(\operatorname{\mathrm{res}}_w\left( \frac{f-\sigma(f)}{f} \right)\right) \mathrel{\Big|} f\in \mathcal{O}_{(L,w)}^\times \right\}\\ &= \left\{ v\left( \frac{f-\sigma(f)}{f} \right) \mathrel{\Big|} f\in \mathcal{O}_{(L,w)}^\times \right\}\cap {\bar{v}(Kw)}_{\infty} \subseteq\Sigma_{L}\cap {\bar{v}(Kw)}_{\infty}, \end{align*} $$
since
![]() $\bar {v}(\operatorname {\mathrm {res}}_w(x))=v(x)$
for
$\bar {v}(\operatorname {\mathrm {res}}_w(x))=v(x)$
for
![]() $x\in L$
such that
$x\in L$
such that
![]() $v(x)\in \bar {v}(Kw)$
.
$v(x)\in \bar {v}(Kw)$
.
Step 2:
![]() $\Sigma _{Lw} \supseteq \Sigma _L \cap {\bar {v}(Kw)}_{\infty }$
.
$\Sigma _{Lw} \supseteq \Sigma _L \cap {\bar {v}(Kw)}_{\infty }$
.
Let
![]() $v\Big (\frac {f-\sigma (f)}{f}\Big )\in \Sigma _L\cap \bar {v}(Kw)$
, i.e.,
$v\Big (\frac {f-\sigma (f)}{f}\Big )\in \Sigma _L\cap \bar {v}(Kw)$
, i.e.,
![]() $f \in L^\times $
, then because
$f \in L^\times $
, then because
![]() $wL=wK$
, there is
$wL=wK$
, there is
![]() $g\in K^\times $
with
$g\in K^\times $
with
![]() $w(f)=w(g)$
and so for
$w(f)=w(g)$
and so for ![]() we have
we have
 $$\begin{align*}\frac{f-\sigma(f)}{f}=\frac{h-\sigma(h)}{h}, \end{align*}$$
$$\begin{align*}\frac{f-\sigma(f)}{f}=\frac{h-\sigma(h)}{h}, \end{align*}$$
so
 $$\begin{align*}v\left(\frac{f-\sigma(f)}{f}\right)=v\left(\frac{h-\sigma(h)}{h}\right)\in\Sigma_{Lw}.\\[-42pt] \end{align*}$$
$$\begin{align*}v\left(\frac{f-\sigma(f)}{f}\right)=v\left(\frac{h-\sigma(h)}{h}\right)\in\Sigma_{Lw}.\\[-42pt] \end{align*}$$
Question 4.9. Let
![]() $(K,v)$
be a henselian valued field with
$(K,v)$
be a henselian valued field with
![]() $v=\bar {v}\circ w$
, such that both
$v=\bar {v}\circ w$
, such that both
![]() $(K,w)$
and
$(K,w)$
and
![]() $(Kw,\bar {v})$
are independent defect fields. Must then
$(Kw,\bar {v})$
are independent defect fields. Must then
![]() $(K,v)$
be an independent defect field?
$(K,v)$
be an independent defect field?
4.3 Defining valuations from independent defect
We now have all the tools needed to build a definable henselian valuation out of an (independent) defect extension. This subsection is structured in several steps:
-
• Theorem 4.11 contains the core of the argument, showing how to deploy an independent defect extension (and its associated convex subgroup) to build a definable valuation.
-
• Corollary 4.14 shows how to go from our assumptions in the Main Theorem to the situation where the right defect extension actually appears.
-
• Corollaries 4.16 and 4.17 then specialize to the mixed characteristic situation, where some extra care is needed.
Finally, in Section 4.4, we will deal with a scenario that mirrors the one of Proposition 3.6, namely with the situation where
![]() $(K,v_K)$
is defectless, but some elementary extension
$(K,v_K)$
is defectless, but some elementary extension
![]() $L$
of
$L$
of
![]() $Kv_K$
is henselian and
$Kv_K$
is henselian and
![]() $v_L$
admits defect.
$v_L$
admits defect.
The following theorem should be thought of as a more elevated version of Lemma 4.2, where the
![]() $\mathcal {L}_{\mathrm {ring}}$
-definable set
$\mathcal {L}_{\mathrm {ring}}$
-definable set
![]() $D$
now appears as a subset of the cartesian product
$D$
now appears as a subset of the cartesian product
![]() $K^p$
, which we identify along an interpretation with a degree
$K^p$
, which we identify along an interpretation with a degree
![]() $p$
Galois defect extension. For details on interpretations of finite field extensions, see, for example, [Reference Chatzidakis3, Section 3.5].
$p$
Galois defect extension. For details on interpretations of finite field extensions, see, for example, [Reference Chatzidakis3, Section 3.5].
We will often use [Reference Jahnke and Koenigsmann9, Theorem 3.10] to reduce to the case where our valuation of interest is in
![]() $H_1$
. We briefly explain how this is done in the following remark.
$H_1$
. We briefly explain how this is done in the following remark.
Remark 4.10. Suppose that
![]() $K$
is not separably closed, and let
$K$
is not separably closed, and let
![]() $v \in H_2(K)$
. Then, [Reference Jahnke and Koenigsmann9, Theorem 3.10] produces a non-trivial
$v \in H_2(K)$
. Then, [Reference Jahnke and Koenigsmann9, Theorem 3.10] produces a non-trivial
![]() $\varnothing $
-definable henselian valuation
$\varnothing $
-definable henselian valuation
![]() $w$
on
$w$
on
![]() $K$
. A closer look at the proof of [Reference Jahnke and Koenigsmann9, Theorem 3.10] allows us to argue that
$K$
. A closer look at the proof of [Reference Jahnke and Koenigsmann9, Theorem 3.10] allows us to argue that
![]() $w$
is a coarsening of
$w$
is a coarsening of
![]() $v$
. If
$v$
. If
![]() $\operatorname {\mathrm {char}}(K) = p> 0$
, or
$\operatorname {\mathrm {char}}(K) = p> 0$
, or
![]() $K$
contains a primitive
$K$
contains a primitive
![]() $p$
th root of unity, then by construction
$p$
th root of unity, then by construction
![]() $w$
is a (possibly non-proper) coarsening of
$w$
is a (possibly non-proper) coarsening of
![]() $v_K$
, and thus in particular of
$v_K$
, and thus in particular of
![]() $v$
. Otherwise, one moves to
$v$
. Otherwise, one moves to
![]() $L = K(\zeta _p)$
for some primitive
$L = K(\zeta _p)$
for some primitive
![]() $p$
th root of unity
$p$
th root of unity
![]() $\zeta _p$
. On
$\zeta _p$
. On
![]() $L$
, one finds a coarsening
$L$
, one finds a coarsening
![]() $w'$
of
$w'$
of
![]() $v_L$
which is
$v_L$
which is
![]() $\varnothing $
-definable and non-trivial. Its restriction
$\varnothing $
-definable and non-trivial. Its restriction ![]() is then a definable coarsening of
is then a definable coarsening of
![]() $v_K$
([Reference Engler and Prestel4, Theorem 4.4.3]—with the caveat that
$v_K$
([Reference Engler and Prestel4, Theorem 4.4.3]—with the caveat that
![]() $H(K)$
means
$H(K)$
means
![]() $H_1(K) \cup \{\mathcal {O}_{v_K}\}$
here).
$H_1(K) \cup \{\mathcal {O}_{v_K}\}$
here).
Theorem 4.11. Let
![]() $(K,v)$
be a henselian valued field with
$(K,v)$
be a henselian valued field with
![]() $\operatorname {\mathrm {char}}{Kv} = p> 0$
such that
$\operatorname {\mathrm {char}}{Kv} = p> 0$
such that
![]() $(K,v)$
admits a Galois extension of degree
$(K,v)$
admits a Galois extension of degree
![]() $p$
with independent defect. If
$p$
with independent defect. If
![]() $\operatorname {\mathrm {char}}(K)=0$
, we additionally assume that
$\operatorname {\mathrm {char}}(K)=0$
, we additionally assume that
![]() $\zeta _p\in K$
, where
$\zeta _p\in K$
, where
![]() $\zeta _p$
is a primitive
$\zeta _p$
is a primitive
![]() $p$
-th root of unity. Then
$p$
-th root of unity. Then
![]() $K$
admits a non-trivial definable henselian valuation, coarsening
$K$
admits a non-trivial definable henselian valuation, coarsening
![]() $v$
.
$v$
.
Proof. Note that we can assume that
![]() $v \in H_1(K)$
, by Remark 4.10. Let
$v \in H_1(K)$
, by Remark 4.10. Let
![]() $K \subseteq L$
be the degree
$K \subseteq L$
be the degree
![]() $p$
Galois extension with independent defect and take
$p$
Galois extension with independent defect and take
![]() $\theta $
such that
$\theta $
such that
![]() $L=K(\theta )$
. Let
$L=K(\theta )$
. Let
![]() $\sigma $
be a generator of the (cyclic) Galois group
$\sigma $
be a generator of the (cyclic) Galois group
![]() ${\operatorname {Gal}({L} | {K})}$
, and let
${\operatorname {Gal}({L} | {K})}$
, and let

As the extension has independent defect, there is a (possibly trivial) convex subgroup
![]() $H \subsetneq vK$
such that
$H \subsetneq vK$
such that
Recall that
![]() $L=K(\theta )$
can be interpreted in
$L=K(\theta )$
can be interpreted in
![]() $K$
via the
$K$
via the
![]() $K$
-linear isomorphism
$K$
-linear isomorphism
 $$\begin{align*}f\colon\left\{ \begin{array}{rcl} K^p & \to & L=K(\theta)\\ (a_0,\ldots,a_{p-1})&\mapsto &\sum_{i=0}^{p-1} a_i\theta^i. \end{array}\right. \end{align*}$$
$$\begin{align*}f\colon\left\{ \begin{array}{rcl} K^p & \to & L=K(\theta)\\ (a_0,\ldots,a_{p-1})&\mapsto &\sum_{i=0}^{p-1} a_i\theta^i. \end{array}\right. \end{align*}$$
Note that the coefficients of the minimal polynomial of the generator
![]() $\theta $
over
$\theta $
over
![]() $K$
are needed as parameters to describe the multiplication. Now, the action of
$K$
are needed as parameters to describe the multiplication. Now, the action of
![]() $\sigma $
is definable in
$\sigma $
is definable in
![]() $K$
(via the interpretation) using the coefficients of the change of basis matrix. If
$K$
(via the interpretation) using the coefficients of the change of basis matrix. If
![]() $\operatorname {\mathrm {char}}(K)=p$
then the matrix has integer coefficients, so no additional parameter is needed. If
$\operatorname {\mathrm {char}}(K)=p$
then the matrix has integer coefficients, so no additional parameter is needed. If
![]() $\operatorname {\mathrm {char}}(K) = 0$
, then we need to use
$\operatorname {\mathrm {char}}(K) = 0$
, then we need to use
![]() $\zeta _p$
. We will denote the parameter tuple needed to define
$\zeta _p$
. We will denote the parameter tuple needed to define
![]() $D$
in
$D$
in
![]() $K$
by
$K$
by
![]() $\overline {c}$
(i.e., the coefficients of the minimal polynomial of the generator
$\overline {c}$
(i.e., the coefficients of the minimal polynomial of the generator
![]() $\theta $
over
$\theta $
over
![]() $K$
, and
$K$
, and
![]() $\zeta _p$
if necessary).
$\zeta _p$
if necessary).
Thus,
![]() $f^{-1}(D) \subseteq K^p$
is definable in
$f^{-1}(D) \subseteq K^p$
is definable in
![]() $K$
, using
$K$
, using
![]() $\overline {c}$
as parameters; choose an
$\overline {c}$
as parameters; choose an
![]() $\mathcal {L}_{\mathrm {ring}}(\overline {c})$
-formula
$\mathcal {L}_{\mathrm {ring}}(\overline {c})$
-formula
![]() $\psi (\overline {X},\overline {c})$
so that
$\psi (\overline {X},\overline {c})$
so that
![]() $f^{-1}(D) = \psi (K^p,\overline {c})$
. Denote by
$f^{-1}(D) = \psi (K^p,\overline {c})$
. Denote by
![]() $\mathcal {O}_H \subseteq L$
the coarsening of (the unique extension of)
$\mathcal {O}_H \subseteq L$
the coarsening of (the unique extension of)
![]() $v$
corresponding to
$v$
corresponding to
![]() $H$
. We can see
$H$
. We can see
![]() $\mathcal {O}_H$
as a subset
$\mathcal {O}_H$
as a subset
![]() $f^{-1}(\mathcal {O}_H)$
of
$f^{-1}(\mathcal {O}_H)$
of
![]() $K^p$
.
$K^p$
.
Claim.
![]() $f^{-1}(\mathcal {O}_H) \subseteq K^p$
is
$f^{-1}(\mathcal {O}_H) \subseteq K^p$
is
![]() $\mathcal {L}_{\mathrm {ring}}(\overline {c})$
-definable.
$\mathcal {L}_{\mathrm {ring}}(\overline {c})$
-definable.
We will use Beth’s definability theorem. We work in ![]() , where
, where
![]() $P(\overline {X})$
is a
$P(\overline {X})$
is a
![]() $p$
-ary predicate. Under the bijection
$p$
-ary predicate. Under the bijection
![]() $f$
that establishes the interpretation, the predicate will represent the valuation subring
$f$
that establishes the interpretation, the predicate will represent the valuation subring
![]() $\mathcal {O}_H$
of
$\mathcal {O}_H$
of
![]() $K(\theta )$
. We now let
$K(\theta )$
. We now let
![]() $(M,\overline {c}^{\prime },P_1),(M,\overline {c}^{\prime },P_2) \equiv _{\mathcal {L}} (K,\overline {c},f^{-1}(\mathcal {O}_H))$
. Note that the interpretation given by
$(M,\overline {c}^{\prime },P_1),(M,\overline {c}^{\prime },P_2) \equiv _{\mathcal {L}} (K,\overline {c},f^{-1}(\mathcal {O}_H))$
. Note that the interpretation given by
![]() $f$
gives rise to an
$f$
gives rise to an
![]() $\mathcal {L}_{\mathrm {ring}}$
-structure
$\mathcal {L}_{\mathrm {ring}}$
-structure
![]() $N$
and a map
$N$
and a map
![]() $f'$
which is establishing an interpretation of
$f'$
which is establishing an interpretation of
![]() $N$
in
$N$
in
![]() $M$
.
$M$
.
Furthermore, because
![]() $(M,\overline {c}^{\prime },P_1)$
and
$(M,\overline {c}^{\prime },P_1)$
and
![]() $(M,\overline {c}^{\prime },P_2)$
are elementarily equivalent, we have that:
$(M,\overline {c}^{\prime },P_2)$
are elementarily equivalent, we have that:
-
•
 $M\subseteq N$
are fields, and the polynomial with coefficients from
$M\subseteq N$
are fields, and the polynomial with coefficients from
 $\overline {c}'$
is of degree
$\overline {c}'$
is of degree
 $p$
and irreducible over
$p$
and irreducible over
 $M$
; thus, the field extension
$M$
; thus, the field extension
 $M\subseteq N$
is algebraic of degree
$M\subseteq N$
is algebraic of degree
 $p$
;
$p$
; -
•
 $\mathcal {O}_1 = f^{\prime }(P_1)$
and
$\mathcal {O}_1 = f^{\prime }(P_1)$
and
 $\mathcal {O}_2 = f'(P_2)$
are non-trivial henselian valuation rings on
$\mathcal {O}_2 = f'(P_2)$
are non-trivial henselian valuation rings on
 $N$
; we denote the corresponding valuations by
$N$
; we denote the corresponding valuations by
 $v_1$
and
$v_1$
and
 $v_2$
, respectively;
$v_2$
, respectively; -
• there is
 $\ell \geq 2$
such that there is a separable polynomial of degree
$\ell \geq 2$
such that there is a separable polynomial of degree
 $\ell $
over
$\ell $
over
 $Lv_H$
with no root in
$Lv_H$
with no root in
 $Lv_H$
; thus, there are separable polynomials of degree
$Lv_H$
; thus, there are separable polynomials of degree
 $\ell $
over
$\ell $
over
 $Nv_1$
and
$Nv_1$
and
 $Nv_2$
with no root, and thus
$Nv_2$
with no root, and thus
 $v_1, v_2 \in H_1(N)$
,
$v_1, v_2 \in H_1(N)$
, -
• for
 $i =1,2$
,
$i =1,2$
,
 $x \notin \mathcal {O}_i$
if and only if there are
$x \notin \mathcal {O}_i$
if and only if there are
 $u \in \mathcal {O}_i^\times $
and
$u \in \mathcal {O}_i^\times $
and
 $y \in \psi (M^p,\overline {c}')$
such that
$y \in \psi (M^p,\overline {c}')$
such that
 $x = u \frac {1}{f'(y)}$
.
$x = u \frac {1}{f'(y)}$
.
Since
![]() $\mathcal {O}_1, \mathcal {O}_2 \in H_1(N)$
, they must be comparable. Assume, for example, that
$\mathcal {O}_1, \mathcal {O}_2 \in H_1(N)$
, they must be comparable. Assume, for example, that
![]() ${\mathcal {O}_1 \subseteq \mathcal {O}_2}$
. Towards a contradiction, assume now that there is
${\mathcal {O}_1 \subseteq \mathcal {O}_2}$
. Towards a contradiction, assume now that there is
![]() $x \in \mathcal {O}_2$
such that
$x \in \mathcal {O}_2$
such that
![]() $x \notin \mathcal {O}_1$
. In particular, this means that there are
$x \notin \mathcal {O}_1$
. In particular, this means that there are
![]() $u \in \mathcal {O}_1^\times $
and
$u \in \mathcal {O}_1^\times $
and
![]() $y \in \psi (M^p,\overline {c}')$
such that
$y \in \psi (M^p,\overline {c}')$
such that
![]() ${x = u\frac {1}{f'(y)}}$
. But since
${x = u\frac {1}{f'(y)}}$
. But since
![]() $\mathcal {O}_1^\times \subseteq \mathcal {O}_2^\times $
, and thus
$\mathcal {O}_1^\times \subseteq \mathcal {O}_2^\times $
, and thus
![]() $u \in \mathcal {O}_2^\times $
, we get that
$u \in \mathcal {O}_2^\times $
, we get that
![]() $x \notin \mathcal {O}_2$
, a contradiction. Then
$x \notin \mathcal {O}_2$
, a contradiction. Then
![]() $\mathcal {O}_1 = \mathcal {O}_2$
, so
$\mathcal {O}_1 = \mathcal {O}_2$
, so
![]() $P_1 = P_2$
and we can apply Beth’s definability. This means that there is an
$P_1 = P_2$
and we can apply Beth’s definability. This means that there is an
![]() $\mathcal {L}_{\mathrm {ring}}$
-formula
$\mathcal {L}_{\mathrm {ring}}$
-formula
![]() $\psi (\overline {X},\overline {c})$
, such that
$\psi (\overline {X},\overline {c})$
, such that
![]() ${f^{-1}(\mathcal {O}_H) = \psi (K^p,\overline {c})}$
.
${f^{-1}(\mathcal {O}_H) = \psi (K^p,\overline {c})}$
.
![]() $\blacksquare _{\text {Claim}}$
$\blacksquare _{\text {Claim}}$
Now, we can define the (non-trivial) restriction
![]() $\mathcal {O}_H \cap K$
as follows: given
$\mathcal {O}_H \cap K$
as follows: given
![]() $z \in K$
, we have that
$z \in K$
, we have that
 $$\begin{align*}z \in \mathcal{O}_H \cap K \iff K \vDash \psi(z, \underbrace{0, \dots, 0}_{(p-1)\text{-times}}, \overline{c}).\end{align*}$$
$$\begin{align*}z \in \mathcal{O}_H \cap K \iff K \vDash \psi(z, \underbrace{0, \dots, 0}_{(p-1)\text{-times}}, \overline{c}).\end{align*}$$
This exhibits a non-trivial definable henselian valuation ring on
![]() $K$
.
$K$
.
We can now use this theorem to define a non-trivial henselian valuation on certain valued fields with defect, but first we need to produce the Galois defect extensions required to exhibit independent defect.
Lemma 4.12. Let
![]() $(K,v)$
be a perfect valued field of residue characteristic
$(K,v)$
be a perfect valued field of residue characteristic
![]() $p> 0$
. If
$p> 0$
. If
![]() $(K,v)$
is not defectless, then there is a finite extension
$(K,v)$
is not defectless, then there is a finite extension
![]() $K \subseteq K'$
such that
$K \subseteq K'$
such that
![]() $K'$
admits a defect Galois extension of degree
$K'$
admits a defect Galois extension of degree
![]() $p$
.
$p$
.
Proof. Take a defect extension
![]() $K \subseteq L$
. In particular,
$K \subseteq L$
. In particular,
![]() $p^n \mid [L:K]$
for some
$p^n \mid [L:K]$
for some
![]() $n \geq 1$
. We let
$n \geq 1$
. We let
![]() $N$
be the normal hull of
$N$
be the normal hull of
![]() $L$
; note that
$L$
; note that
![]() $p^n \mid [N:K]$
and
$p^n \mid [N:K]$
and
![]() $K \subseteq N$
is Galois. Consider now
$K \subseteq N$
is Galois. Consider now
![]() $H \subseteq {\operatorname {Gal}({N} | {K})}$
to be a
$H \subseteq {\operatorname {Gal}({N} | {K})}$
to be a
![]() $p$
-Sylow subgroup. Then
$p$
-Sylow subgroup. Then ![]() is such that
is such that
![]() $L' \subseteq N$
is Galois and it is a tower
$L' \subseteq N$
is Galois and it is a tower
![]() $L' = L_0 \subseteq L_1 \subseteq \cdots \subseteq L_n = N$
of normal degree
$L' = L_0 \subseteq L_1 \subseteq \cdots \subseteq L_n = N$
of normal degree
![]() $p$
extensions. Moreover, since
$p$
extensions. Moreover, since
![]() $K \subseteq L'$
has degree prime to
$K \subseteq L'$
has degree prime to
![]() $p$
, it is defectless, hence
$p$
, it is defectless, hence
![]() $L' \subseteq N$
is defect. In particular, there is some
$L' \subseteq N$
is defect. In particular, there is some
![]() $\ell \leq n$
such that
$\ell \leq n$
such that
![]() $L_\ell \subseteq L_{\ell +1}$
is a defect Galois extension of degree
$L_\ell \subseteq L_{\ell +1}$
is a defect Galois extension of degree
![]() $p$
, so we take
$p$
, so we take
![]() $K' = L_{\ell }$
.
$K' = L_{\ell }$
.
Remark 4.13. Note that if
![]() $F \subseteq E$
is a finite separable field extension of degree
$F \subseteq E$
is a finite separable field extension of degree
![]() $n$
, we can interpret
$n$
, we can interpret
![]() $E$
inside of
$E$
inside of
![]() $F$
using the coefficients
$F$
using the coefficients
![]() $\overline {c}$
of the minimal polynomial of a primitive element of the extension. Suppose we had a definable valuation
$\overline {c}$
of the minimal polynomial of a primitive element of the extension. Suppose we had a definable valuation
![]() $v$
on
$v$
on
![]() $E$
, say defined by
$E$
, say defined by
![]() $\varphi (X,\overline {d})$
. Using the interpretation we can define
$\varphi (X,\overline {d})$
. Using the interpretation we can define
![]() $\mathcal {O}_v$
(as a subset of
$\mathcal {O}_v$
(as a subset of
![]() $F^n$
) using some other formula
$F^n$
) using some other formula
![]() $\widetilde {\varphi }(\overline {X},\overline {d'})$
, where now
$\widetilde {\varphi }(\overline {X},\overline {d'})$
, where now
![]() $\overline {d'}$
is given by the coordinates of the elements of
$\overline {d'}$
is given by the coordinates of the elements of
![]() $\overline {d}$
in a fixed
$\overline {d}$
in a fixed
![]() $F$
-basis of
$F$
-basis of
![]() $F^n$
, together with
$F^n$
, together with
![]() $\overline {c}$
. The restriction
$\overline {c}$
. The restriction
![]() $v\vert _F$
can then be defined using the formula
$v\vert _F$
can then be defined using the formula

Corollary 4.14. Suppose
![]() $(K,v)$
is a henselian valued field with
$(K,v)$
is a henselian valued field with
![]() $\operatorname {\mathrm {char}}{Kv} = p> 0$
such that
$\operatorname {\mathrm {char}}{Kv} = p> 0$
such that
![]() $(K,v)$
is not defectless, and such that either:
$(K,v)$
is not defectless, and such that either:
-
(1)
 $K$
is perfect, if
$K$
is perfect, if
 $\operatorname {\mathrm {char}}{K} = p> 0$
, or
$\operatorname {\mathrm {char}}{K} = p> 0$
, or -
(2)
 $\mathcal {O}_v/p$
is semi-perfect, if
$\mathcal {O}_v/p$
is semi-perfect, if
 $\operatorname {\mathrm {char}}{K} = 0$
.
$\operatorname {\mathrm {char}}{K} = 0$
.
Then
![]() $K$
admits a non-trivial definable henselian valuation, coarsening
$K$
admits a non-trivial definable henselian valuation, coarsening
![]() $v$
.
$v$
.
Proof. We may assume that
![]() $v \in H_1(K)$
, by Remark 4.10.
$v \in H_1(K)$
, by Remark 4.10.
In the case where
![]() $\operatorname {\mathrm {char}}{K} = 0$
, we make the following two observations:
$\operatorname {\mathrm {char}}{K} = 0$
, we make the following two observations:
-
• Since
 $K$
always admits a definable valuation if
$K$
always admits a definable valuation if
 $v$
is finitely ramified, we may assume that it is infinitely ramified.
$v$
is finitely ramified, we may assume that it is infinitely ramified. -
• The assumptions on
 $(K,v)$
imply that it is a roughly deeply ramified valued field in the sense of [Reference Kuhlmann and Rzepka16, p. 2696] (note that by [Reference Kuhlmann and Rzepka16, Lemma 4.1], we only need to check that
$(K,v)$
imply that it is a roughly deeply ramified valued field in the sense of [Reference Kuhlmann and Rzepka16, p. 2696] (note that by [Reference Kuhlmann and Rzepka16, Lemma 4.1], we only need to check that
 $\mathcal {O}_{v}/p$
is semi-perfect, without looking at the completion of
$\mathcal {O}_{v}/p$
is semi-perfect, without looking at the completion of
 $K$
). Thus, by [Reference Kuhlmann and Rzepka16, Theorem 1.8] any finite extension of it is also roughly deeply ramified.
$K$
). Thus, by [Reference Kuhlmann and Rzepka16, Theorem 1.8] any finite extension of it is also roughly deeply ramified.
If
![]() $\operatorname {\mathrm {char}}{K} = 0$
, let
$\operatorname {\mathrm {char}}{K} = 0$
, let
![]() $K_0 = K(\zeta _p)$
, where
$K_0 = K(\zeta _p)$
, where
![]() $\zeta _p$
is some primitive
$\zeta _p$
is some primitive
![]() $p$
th root of unity. Otherwise, take
$p$
th root of unity. Otherwise, take
![]() $K_0 = K$
. By Lemma 4.12, we have a finite extension
$K_0 = K$
. By Lemma 4.12, we have a finite extension
![]() $K_0 \subseteq K_1$
which admits a Galois defect extension of degree
$K_0 \subseteq K_1$
which admits a Galois defect extension of degree
![]() $p$
. Since
$p$
. Since
![]() $K\subseteq K_1$
is a finite separable field extension, we can find
$K\subseteq K_1$
is a finite separable field extension, we can find
![]() $b\in K_1$
such that
$b\in K_1$
such that
![]() $K_1=K(b)$
.
$K_1=K(b)$
.
The field
![]() $K_1$
admits a Galois defect extension of degree
$K_1$
admits a Galois defect extension of degree
![]() $p$
, i.e there is
$p$
, i.e there is
![]() $c \in K_1$
which has no Artin–Schreier root in
$c \in K_1$
which has no Artin–Schreier root in
![]() $K$
if
$K$
if
![]() $\operatorname {\mathrm {char}}{K} = p$
(resp. no
$\operatorname {\mathrm {char}}{K} = p$
(resp. no
![]() $p$
th root, if
$p$
th root, if
![]() $\operatorname {\mathrm {char}}{K} = 0$
), and the extension
$\operatorname {\mathrm {char}}{K} = 0$
), and the extension
![]() $(K_1,v) \subseteq (K_1(\theta ),v)$
, where
$(K_1,v) \subseteq (K_1(\theta ),v)$
, where
![]() $\theta ^p-\theta = c$
(resp.
$\theta ^p-\theta = c$
(resp.
![]() $\theta ^p = c$
), is an immediate defect extension. Denote by
$\theta ^p = c$
), is an immediate defect extension. Denote by
![]() $L = K_1(\theta )=K(b,\theta )$
. Then, we have to distinguish two cases:
$L = K_1(\theta )=K(b,\theta )$
. Then, we have to distinguish two cases:
-
• If
 $\operatorname {\mathrm {char}}{K} = p$
, then
$\operatorname {\mathrm {char}}{K} = p$
, then
 $K_1$
is a perfect field.
$K_1$
is a perfect field. -
• If
 $\operatorname {\mathrm {char}}{K} = 0$
, then
$\operatorname {\mathrm {char}}{K} = 0$
, then
 $K_1$
is a finite extension of a roughly deeply ramified field, and thus it is roughly deeply ramified itself.
$K_1$
is a finite extension of a roughly deeply ramified field, and thus it is roughly deeply ramified itself.
In both cases,
![]() $K_1$
is an independent defect field (see [Reference Kuhlmann and Rzepka16, Theorem 1.10]), and thus the extension
$K_1$
is an independent defect field (see [Reference Kuhlmann and Rzepka16, Theorem 1.10]), and thus the extension
![]() $(K_1,v) \subseteq (L,v)$
is a degree
$(K_1,v) \subseteq (L,v)$
is a degree
![]() $p$
defect extension with independent defect. By Theorem 4.11, then,
$p$
defect extension with independent defect. By Theorem 4.11, then,
![]() $K_1$
admits a non-trivial definable henselian valuation
$K_1$
admits a non-trivial definable henselian valuation
![]() $v_H$
, with valuation ring defined by
$v_H$
, with valuation ring defined by
![]() $\varphi (X,\overline {c})$
. As
$\varphi (X,\overline {c})$
. As
![]() $K_1=K(b)$
can be interpreted in
$K_1=K(b)$
can be interpreted in
![]() $K$
, by Remark 4.13 the restriction of
$K$
, by Remark 4.13 the restriction of
![]() $v_H$
to
$v_H$
to
![]() $K$
is then
$K$
is then
![]() $\mathcal {L}_{\mathrm {ring}}$
-definable with parameters (namely, the coefficients of the minimal polynomial of
$\mathcal {L}_{\mathrm {ring}}$
-definable with parameters (namely, the coefficients of the minimal polynomial of
![]() $b$
, and the coordinates of
$b$
, and the coordinates of
![]() $\overline {c}$
in a chosen
$\overline {c}$
in a chosen
![]() $K$
-basis of
$K$
-basis of
![]() $K_1$
).
$K_1$
).
As we will later have to deal with definable valuations in some ultrapower of our field
![]() $K$
, we immediately apply results of Anscombe and Jahnke from [Reference Anscombe and Jahnke1] to get rid of parameters in our definition.
$K$
, we immediately apply results of Anscombe and Jahnke from [Reference Anscombe and Jahnke1] to get rid of parameters in our definition.
Remark 4.15. Note that if
![]() $(K,v)$
is a henselian valued field of mixed characteristic, with
$(K,v)$
is a henselian valued field of mixed characteristic, with
![]() $v \in H_1(K)$
, then
$v \in H_1(K)$
, then
![]() $v_K$
is also of mixed characteristic.
$v_K$
is also of mixed characteristic.
Corollary 4.16. Suppose
![]() $(K,v)$
is a henselian valued field of mixed characteristic, such that
$(K,v)$
is a henselian valued field of mixed characteristic, such that
![]() $(K,v)$
is not defectless and
$(K,v)$
is not defectless and
![]() $\mathcal {O}_v/p$
is semi-perfect. Then
$\mathcal {O}_v/p$
is semi-perfect. Then
![]() $K$
admits an
$K$
admits an
![]() $\varnothing $
-definable non-trivial henselian valuation.
$\varnothing $
-definable non-trivial henselian valuation.
Proof. We may assume that
![]() $v \in H_1(K)$
, by Remark 4.10. Now,
$v \in H_1(K)$
, by Remark 4.10. Now,
![]() $v_K$
is also of mixed characteristic, thus Corollary 4.14 yields the existence of a definable non-trivial henselian valuation, and by [Reference Anscombe and Jahnke1, Theorem 1.1(B)] we can conclude that there is an
$v_K$
is also of mixed characteristic, thus Corollary 4.14 yields the existence of a definable non-trivial henselian valuation, and by [Reference Anscombe and Jahnke1, Theorem 1.1(B)] we can conclude that there is an
![]() $\varnothing $
-definable non-trivial henselian one.
$\varnothing $
-definable non-trivial henselian one.
Later, in the proof of Proposition 4.18, we will find ourselves in the situation where we deal with a defect refinement
![]() $v_1$
of a valuation
$v_1$
of a valuation
![]() $v_K^{\mathcal U}$
, where
$v_K^{\mathcal U}$
, where
![]() $K^{\mathcal U}v_K^{\mathcal {U}}$
is perfect.
$K^{\mathcal U}v_K^{\mathcal {U}}$
is perfect.
Lemma 4.17. Suppose
![]() $(K,v)$
is a henselian valued field of mixed characteristic, such that
$(K,v)$
is a henselian valued field of mixed characteristic, such that
![]() $(K,v)$
is not defectless, and there is a coarsening
$(K,v)$
is not defectless, and there is a coarsening
![]() $w$
of
$w$
of
![]() $v$
such that
$v$
such that
![]() $(K,w)$
is defectless and
$(K,w)$
is defectless and
![]() $Kw$
is perfect of characteristic
$Kw$
is perfect of characteristic
![]() $p>0$
. Then
$p>0$
. Then
![]() $K$
admits an
$K$
admits an
![]() $\varnothing $
-definable non-trivial henselian valuation.
$\varnothing $
-definable non-trivial henselian valuation.
Proof. We may assume that
![]() $v \in H_1(K)$
: otherwise, we can use [Reference Jahnke and Koenigsmann9, Theorem 3.10] to find an
$v \in H_1(K)$
: otherwise, we can use [Reference Jahnke and Koenigsmann9, Theorem 3.10] to find an
![]() $\varnothing $
-definable non-trivial henselian valuation. Using Lemma 4.12, there is a finite extension
$\varnothing $
-definable non-trivial henselian valuation. Using Lemma 4.12, there is a finite extension
![]() $K(\zeta _p) \subseteq K_1$
such that
$K(\zeta _p) \subseteq K_1$
such that
![]() $(K_1,v)$
admits a defect extension of degree
$(K_1,v)$
admits a defect extension of degree
![]() $p$
, and we find
$p$
, and we find
![]() $b\in K_1$
such that
$b\in K_1$
such that
![]() $K_1=K(b)$
.
$K_1=K(b)$
.
We now show that
![]() $(K_1,v)$
is an independent defect field. For this we consider the decomposition of
$(K_1,v)$
is an independent defect field. For this we consider the decomposition of
![]() $(K_1,v)$
with respect to the coarsening
$(K_1,v)$
with respect to the coarsening
![]() $(K_1,w)$
and we denote the induced valuation on
$(K_1,w)$
and we denote the induced valuation on
![]() $K_1w$
by
$K_1w$
by
![]() $\bar {v}$
:
$\bar {v}$
:

Note that
![]() $(K_1,w)$
is defectless, because it is a finite extension of
$(K_1,w)$
is defectless, because it is a finite extension of
![]() $(K,w)$
and
$(K,w)$
and
![]() $K_1w$
is perfect because it is a finite extension of
$K_1w$
is perfect because it is a finite extension of
![]() $Kw$
. From Lemma 4.8 it follows that also
$Kw$
. From Lemma 4.8 it follows that also
![]() $(K_1,v)$
is an independent defect field.
$(K_1,v)$
is an independent defect field.
By Theorem 4.11, then,
![]() $K_1$
admits a non-trivial definable henselian valuation
$K_1$
admits a non-trivial definable henselian valuation
![]() $v_H$
, with valuation ring defined by
$v_H$
, with valuation ring defined by
![]() $\varphi (X,\overline {c})$
. As
$\varphi (X,\overline {c})$
. As
![]() $K_1=K(b)$
can be interpreted in
$K_1=K(b)$
can be interpreted in
![]() $K$
, by Remark 4.13 the restriction of
$K$
, by Remark 4.13 the restriction of
![]() $v_H$
to
$v_H$
to
![]() $K$
is then
$K$
is then
![]() $\mathcal {L}_{\mathrm {ring}}$
-definable with parameters (namely, the coefficients of the minimal polynomial of
$\mathcal {L}_{\mathrm {ring}}$
-definable with parameters (namely, the coefficients of the minimal polynomial of
![]() $b$
, and the coordinates of
$b$
, and the coordinates of
![]() $\overline {c}$
in a chosen
$\overline {c}$
in a chosen
![]() $K$
-basis of
$K$
-basis of
![]() $K_1$
).
$K_1$
).
By our assumptions,
![]() $v_K$
is also of mixed characteristic, thus [Reference Anscombe and Jahnke1, Theorem 1.1(B)] yields the existence of an
$v_K$
is also of mixed characteristic, thus [Reference Anscombe and Jahnke1, Theorem 1.1(B)] yields the existence of an
![]() $\varnothing $
-definable non-trivial henselian valuation.
$\varnothing $
-definable non-trivial henselian valuation.
4.4 Defect in elementary extensions of
 $Kv_K$
$Kv_K$
The following proposition is a direct result of Lemma 4.17, while we will need some more work for positive characteristic.
Proposition 4.18. Let
![]() $K$
be a henselian field such that
$K$
be a henselian field such that
![]() $(K,v_K)$
has mixed characteristic and
$(K,v_K)$
has mixed characteristic and
![]() $Kv_K$
is perfect. If:
$Kv_K$
is perfect. If:
-
(1) there is
 $L\equiv Kv_K$
such that
$L\equiv Kv_K$
such that
 $(L,v_L)$
is not defectless, and
$(L,v_L)$
is not defectless, and -
(2)
 $(K,v_K)$
is defectless,
$(K,v_K)$
is defectless,
then
![]() $K$
admits an
$K$
admits an
![]() $\varnothing $
-definable non-trivial henselian valuation.
$\varnothing $
-definable non-trivial henselian valuation.
Proof. Choose
![]() $L$
such that
$L$
such that
![]() $L\equiv Kv_K$
and
$L\equiv Kv_K$
and
![]() $(L,v_L)$
is not defectless. By the Keisler–Shelah isomorphism theorem [Reference Marker17, Theorem 2.5.36], take an index set
$(L,v_L)$
is not defectless. By the Keisler–Shelah isomorphism theorem [Reference Marker17, Theorem 2.5.36], take an index set
![]() $I$
and an ultrafilter
$I$
and an ultrafilter
![]() $\mathcal U$
on
$\mathcal U$
on
![]() $I$
such that
$I$
such that
![]() $(Kv_K)^{\mathcal U} \cong L^{\mathcal U}$
. Consider the ultrapowers
$(Kv_K)^{\mathcal U} \cong L^{\mathcal U}$
. Consider the ultrapowers ![]() and
and ![]() in
in
![]() $\mathcal {L}_{\mathrm {val}}$
. Since
$\mathcal {L}_{\mathrm {val}}$
. Since
![]() $v_L^{\mathcal U}$
is a valuation with defect, while
$v_L^{\mathcal U}$
is a valuation with defect, while
![]() $v_K^{\mathcal U}$
is defectless, the composition
$v_K^{\mathcal U}$
is defectless, the composition
![]() $v_1$
is a non-trivial henselian valuation on
$v_1$
is a non-trivial henselian valuation on
![]() $K^{\mathcal U}$
with defect. The valuation
$K^{\mathcal U}$
with defect. The valuation
![]() $v_1$
is not defectless and of mixed characteristic, since
$v_1$
is not defectless and of mixed characteristic, since
![]() $v_K^{\mathcal {U}}$
is, and its coarsening
$v_K^{\mathcal {U}}$
is, and its coarsening
![]() $v_K^{\mathcal {U}}$
is defectless and has perfect residue field
$v_K^{\mathcal {U}}$
is defectless and has perfect residue field
![]() $K^{\mathcal {U}}v_K^{\mathcal {U}}=L^{\mathcal {U}}$
. Thus by Lemma 4.17, there is an
$K^{\mathcal {U}}v_K^{\mathcal {U}}=L^{\mathcal {U}}$
. Thus by Lemma 4.17, there is an
![]() $\varnothing $
-definable valuation on
$\varnothing $
-definable valuation on
![]() $K^{\mathcal {U}}$
. By elementary equivalence, we can find an
$K^{\mathcal {U}}$
. By elementary equivalence, we can find an
![]() $\varnothing $
-definable henselian valuation on
$\varnothing $
-definable henselian valuation on
![]() $K$
.
$K$
.
In the case of positive characteristic, eliminating the parameters from the definition of the henselian valuation can be tricky; indeed, a theorem along the lines of [Reference Anscombe and Jahnke1, Theorem 1.1(B)] will not be true in general in positive characteristic. However, in our setting (particularly because we can assume
![]() $v_KK$
to be divisible) we manage to get an analogous result, where we take a valuation defined in an elementary extension
$v_KK$
to be divisible) we manage to get an analogous result, where we take a valuation defined in an elementary extension
![]() $K \preceq K^*$
(with parameters possibly in
$K \preceq K^*$
(with parameters possibly in
![]() $K^*$
) and produce a valuation defined with parameters in
$K^*$
) and produce a valuation defined with parameters in
![]() $K$
, thus allowing us to “push it down”.
$K$
, thus allowing us to “push it down”.
Fact 4.19 (cf. [Reference Jahnke8, Proposition 2.4]).
Let
![]() $(K,v)$
be a henselian valued field with non-separably closed nor real closed residue field. Then
$(K,v)$
be a henselian valued field with non-separably closed nor real closed residue field. Then
![]() $v$
has an
$v$
has an
![]() $\mathcal {L}_{\mathrm {ring}}$
-definable refinement.
$\mathcal {L}_{\mathrm {ring}}$
-definable refinement.
Proposition 4.20. Let
![]() $K$
be a perfect henselian field of positive characteristic. If:
$K$
be a perfect henselian field of positive characteristic. If:
-
(1)
 $v_KK$
is divisible, and
$v_KK$
is divisible, and -
(2) there is
 $L\equiv Kv_K$
such that
$L\equiv Kv_K$
such that
 $(L,v_L)$
is not defectless, and
$(L,v_L)$
is not defectless, and -
(3)
 $(K,v_K)$
is defectless,
$(K,v_K)$
is defectless,
then
![]() $K$
admits a definable non-trivial henselian valuation.
$K$
admits a definable non-trivial henselian valuation.
Proof. Note that we may assume that
![]() $Kv_K$
is not separably closed; otherwise, Theorem 2.8 gives an
$Kv_K$
is not separably closed; otherwise, Theorem 2.8 gives an
![]() $\varnothing $
-definable non-trivial henselian valuation.
$\varnothing $
-definable non-trivial henselian valuation.
By the Keisler–Shelah isomorphism theorem [Reference Marker17, Theorem 2.5.36], take an index set
![]() $I$
and an ultrafilter
$I$
and an ultrafilter
![]() $\mathcal U$
on
$\mathcal U$
on
![]() $I$
such that
$I$
such that
![]() ${(Kv_K)^{\mathcal U} \cong L^{\mathcal U}}$
. Consider the ultrapowers
${(Kv_K)^{\mathcal U} \cong L^{\mathcal U}}$
. Consider the ultrapowers ![]() and
and ![]() in
in
![]() $\mathcal{L}_{\mathrm{val}}$
. Since
$\mathcal{L}_{\mathrm{val}}$
. Since
![]() $v_L^{\mathcal U}$
is a valuation with defect, the composition
$v_L^{\mathcal U}$
is a valuation with defect, the composition
![]() $v_1=v_L^{\mathcal U}\circ v_K^{\mathcal U}$
is a non-trivial henselian valuation on
$v_1=v_L^{\mathcal U}\circ v_K^{\mathcal U}$
is a non-trivial henselian valuation on
![]() $K^{\mathcal U}$
with defect. Thus, by Corollary 4.14, there is an
$K^{\mathcal U}$
with defect. Thus, by Corollary 4.14, there is an
![]() $\mathcal {L}_{\mathrm {ring}}(K^{\mathcal U})$
-definable non-trivial henselian valuation
$\mathcal {L}_{\mathrm {ring}}(K^{\mathcal U})$
-definable non-trivial henselian valuation
![]() $v_1^{\prime }$
coarsening
$v_1^{\prime }$
coarsening
![]() $v_1$
, say given by
$v_1$
, say given by
![]() $\varphi (K^{\mathcal U},\overline {\beta })$
for some parameters
$\varphi (K^{\mathcal U},\overline {\beta })$
for some parameters
![]() $\overline {\beta } \in (K^{\mathcal U})^\ell $
,
$\overline {\beta } \in (K^{\mathcal U})^\ell $
,
![]() $\ell \geq 1$
.
$\ell \geq 1$
.
Since
![]() $Kv_K$
is not separably closed, Fact 4.19 yields an
$Kv_K$
is not separably closed, Fact 4.19 yields an
![]() $\mathcal {L}_{\mathrm {ring}}(K)$
-definable valuation
$\mathcal {L}_{\mathrm {ring}}(K)$
-definable valuation
![]() $w$
on
$w$
on
![]() $K$
(not necessarily henselian!) such that
$K$
(not necessarily henselian!) such that
![]() $\mathcal {O}_w \subseteq \mathcal {O}_{v_K}$
. Let
$\mathcal {O}_w \subseteq \mathcal {O}_{v_K}$
. Let
![]() $\psi (X,\overline {c})$
be the formula defining
$\psi (X,\overline {c})$
be the formula defining
![]() $w$
. Denote by
$w$
. Denote by
![]() $w^*$
the valuation corresponding to
$w^*$
the valuation corresponding to
![]() $\psi (K^{\mathcal U},\overline {c})$
. Note that since
$\psi (K^{\mathcal U},\overline {c})$
. Note that since
![]() $(K,v_K) \preceq (K^{\mathcal U}, v_K^{\mathcal U})$
, then we still have that
$(K,v_K) \preceq (K^{\mathcal U}, v_K^{\mathcal U})$
, then we still have that
![]() $w^*$
is a proper refinement of
$w^*$
is a proper refinement of
![]() $v_K^{\mathcal U}$
.
$v_K^{\mathcal U}$
.
As in the proof of [Reference Engler and Prestel4, Theorem 2.3.4], given two valuation rings
![]() $\mathcal {O}_1$
and
$\mathcal {O}_1$
and
![]() $\mathcal {O}_2$
, we let
$\mathcal {O}_2$
, we let

Note that
![]() $\mathcal {O}_1 \cdot \mathcal {O}_2$
contains both
$\mathcal {O}_1 \cdot \mathcal {O}_2$
contains both
![]() $\mathcal {O}_1$
and
$\mathcal {O}_1$
and
![]() $\mathcal {O}_2$
and is always a valuation ring. Indeed, it is the finest valuation ring containing both: if
$\mathcal {O}_2$
and is always a valuation ring. Indeed, it is the finest valuation ring containing both: if
![]() $\mathcal {O}_1, \mathcal {O}_2 \subseteq \mathcal {O}_3$
, then for any
$\mathcal {O}_1, \mathcal {O}_2 \subseteq \mathcal {O}_3$
, then for any
![]() $x \in \mathcal {O}_1$
and
$x \in \mathcal {O}_1$
and
![]() $y \in \mathcal {O}_1 \setminus \mathfrak {m}_2$
, one has that
$y \in \mathcal {O}_1 \setminus \mathfrak {m}_2$
, one has that
![]() $y \notin \mathfrak {m}_3$
, so
$y \notin \mathfrak {m}_3$
, so
![]() $\frac {1}{y} \in \mathcal {O}_3$
and thus
$\frac {1}{y} \in \mathcal {O}_3$
and thus
![]() $\frac {x}{y} \in \mathcal {O}_3$
. We now consider the
$\frac {x}{y} \in \mathcal {O}_3$
. We now consider the
![]() $\mathcal {L}_{\mathrm {ring}}(\overline {c})$
-definable set
$\mathcal {L}_{\mathrm {ring}}(\overline {c})$
-definable set
For each
![]() $\overline {b} \in X$
, we consider the
$\overline {b} \in X$
, we consider the
![]() $\mathcal {L}_{\mathrm {ring}}(\overline {c},\overline {b})$
-definable valuation ring
$\mathcal {L}_{\mathrm {ring}}(\overline {c},\overline {b})$
-definable valuation ring
with corresponding valuation
![]() $v_{\overline {b}}$
. As all coarsenings of a given valuation are comparable, any
$v_{\overline {b}}$
. As all coarsenings of a given valuation are comparable, any
![]() $v_{\overline {b}}$
for
$v_{\overline {b}}$
for
![]() $\overline {b} \in X$
is comparable with
$\overline {b} \in X$
is comparable with
![]() $\mathcal {O}_{v_K^{\mathcal {U}}}$
.
$\mathcal {O}_{v_K^{\mathcal {U}}}$
.
Since
![]() $v_K^{\mathcal U}$
is a tame valuation with divisible value group, Lemma 3.4 implies that
$v_K^{\mathcal U}$
is a tame valuation with divisible value group, Lemma 3.4 implies that
![]() $v_{\overline {b}}$
cannot be a proper coarsening. In particular, then,
$v_{\overline {b}}$
cannot be a proper coarsening. In particular, then,
![]() $\mathcal {O}_{v_{\overline {b}}} \subseteq \mathcal {O}_{v_K^{\mathcal U}}$
. It follows that the union
$\mathcal {O}_{v_{\overline {b}}} \subseteq \mathcal {O}_{v_K^{\mathcal U}}$
. It follows that the union
is a non-trivial
![]() $\mathcal {L}_{\mathrm {ring}}(\overline {c})$
-definable (note the parameters!) valuation ring on
$\mathcal {L}_{\mathrm {ring}}(\overline {c})$
-definable (note the parameters!) valuation ring on
![]() $K^{\mathcal U}$
.
$K^{\mathcal U}$
.
To show that
![]() $\mathcal {O}$
is henselian, we will show that
$\mathcal {O}$
is henselian, we will show that
![]() $\mathcal {O}$
contains
$\mathcal {O}$
contains
![]() $\varphi (K^{\mathcal {U}},\overline {\beta })$
, i.e., that
$\varphi (K^{\mathcal {U}},\overline {\beta })$
, i.e., that
![]() $\overline {\beta } \in X$
. It is enough to show that
$\overline {\beta } \in X$
. It is enough to show that
![]() ${\mathcal {O}_{\overline {\beta }} \neq K^{\mathcal U}}$
. Since
${\mathcal {O}_{\overline {\beta }} \neq K^{\mathcal U}}$
. Since
![]() $\varphi (K^{\mathcal U},\overline {\beta })$
is comparable with
$\varphi (K^{\mathcal U},\overline {\beta })$
is comparable with
![]() $v_K^{\mathcal U}$
, we have two possible cases. Either
$v_K^{\mathcal U}$
, we have two possible cases. Either
![]() $\varphi (K^{\mathcal U},\overline {\beta })$
is coarser than
$\varphi (K^{\mathcal U},\overline {\beta })$
is coarser than
![]() $v_K^{\mathcal U}$
, in which case
$v_K^{\mathcal U}$
, in which case
![]() $\mathcal {O}_{\overline {\beta }} = \varphi (K^{\mathcal {U}},\overline {\beta })$
, or
$\mathcal {O}_{\overline {\beta }} = \varphi (K^{\mathcal {U}},\overline {\beta })$
, or
![]() $\varphi (K^{\mathcal U},\overline {\beta })$
is finer than
$\varphi (K^{\mathcal U},\overline {\beta })$
is finer than
![]() $v_K^{\mathcal U}$
, in which case
$v_K^{\mathcal U}$
, in which case
![]() $\mathcal {O}_{\overline {\beta }}$
is also a refinement of
$\mathcal {O}_{\overline {\beta }}$
is also a refinement of
![]() $v_K^{\mathcal {U}}$
. Either way,
$v_K^{\mathcal {U}}$
. Either way,
![]() $\mathcal {O}_{\overline {\beta }}$
is non-trivial.
$\mathcal {O}_{\overline {\beta }}$
is non-trivial.
We have just shown that
![]() $\mathcal {O}$
is a coarsening of
$\mathcal {O}$
is a coarsening of
![]() $\varphi (K^{\mathcal {U}},\overline {\beta })$
, thus it is henselian. In particular, the same formula defines a non-trivial henselian valuation on
$\varphi (K^{\mathcal {U}},\overline {\beta })$
, thus it is henselian. In particular, the same formula defines a non-trivial henselian valuation on
![]() $K$
, as needed.
$K$
, as needed.
5 Proof of the main theorem
Main theorem. Let
![]() $K$
be perfect, not separably closed, and henselian. If
$K$
be perfect, not separably closed, and henselian. If
![]() ${\operatorname {\mathrm {char}}{K} = 0}$
and
${\operatorname {\mathrm {char}}{K} = 0}$
and
![]() ${\operatorname {\mathrm {char}}{Kv_K} = p> 0}$
, assume that
${\operatorname {\mathrm {char}}{Kv_K} = p> 0}$
, assume that
![]() $\mathcal {O}_{v_K}/p$
is semi-perfect. Then
$\mathcal {O}_{v_K}/p$
is semi-perfect. Then
![]() $K$
admits a definable non-trivial henselian valuation if and only if at least one of the following conditions hold:
$K$
admits a definable non-trivial henselian valuation if and only if at least one of the following conditions hold:
-
(1)
 $Kv_K$
is separably closed,
$Kv_K$
is separably closed, -
(2)
 $Kv_K$
is not t-henselian,
$Kv_K$
is not t-henselian, -
(3) there is
 $L \succeq Kv_K$
such that
$L \succeq Kv_K$
such that
 $v_LL$
is not divisible,
$v_LL$
is not divisible, -
(4)
 $v_KK$
is not divisible,
$v_KK$
is not divisible, -
(5)
 $(K,v_K)$
is not defectless,
$(K,v_K)$
is not defectless, -
(6) there is
 $L \succeq Kv_K$
such that
$L \succeq Kv_K$
such that
 $(L,v_L)$
is not defectless.
$(L,v_L)$
is not defectless.
Proof. If
![]() $\operatorname {\mathrm {char}}{Kv_K} = 0$
, the statement is exactly Theorem 1.1. This is because condition
$\operatorname {\mathrm {char}}{Kv_K} = 0$
, the statement is exactly Theorem 1.1. This is because condition
![]() $5$
is trivial (as equicharacteristic zero henselian valued fields are defectless), and Corollary 2.3 shows that condition
$5$
is trivial (as equicharacteristic zero henselian valued fields are defectless), and Corollary 2.3 shows that condition
![]() $6$
is also trivial in this case.
$6$
is also trivial in this case.
Assume
![]() $\operatorname {\mathrm {char}}{K}v_K = p>0$
and note that
$\operatorname {\mathrm {char}}{K}v_K = p>0$
and note that
![]() $Kv_K$
is perfect: in mixed characteristic,
$Kv_K$
is perfect: in mixed characteristic,
![]() $Kv_K$
is perfect since
$Kv_K$
is perfect since
![]() $\mathcal {O}_{v_K}/p$
is semi-perfect; in positive characteristic,
$\mathcal {O}_{v_K}/p$
is semi-perfect; in positive characteristic,
![]() $Kv_K$
is perfect since
$Kv_K$
is perfect since
![]() $K$
is. Thus, one direction is Theorem 3.5.
$K$
is. Thus, one direction is Theorem 3.5.
In the other direction, we do a case distinction. First, assume
![]() $1 \vee 2 \vee 4$
, then it follows from Theorem 2.8 that
$1 \vee 2 \vee 4$
, then it follows from Theorem 2.8 that
![]() $K$
admits a definable non-trivial henselian valuation.
$K$
admits a definable non-trivial henselian valuation.
If
![]() $3 \wedge \neg 4$
then Proposition 3.6 yields a existence of definable non-trivial henselian valuation.
$3 \wedge \neg 4$
then Proposition 3.6 yields a existence of definable non-trivial henselian valuation.
Suppose now that
![]() $5$
holds, i.e.,
$5$
holds, i.e.,
![]() $(K,v_K)$
is not defectless. Then we get a non-trivial definable henselian valuation from Corollary 4.14.
$(K,v_K)$
is not defectless. Then we get a non-trivial definable henselian valuation from Corollary 4.14.
Finally, assume that
![]() $6$
holds, and since we have already established the case where
$6$
holds, and since we have already established the case where
![]() $1 \vee 2 \vee 3 \vee 4 \vee 5$
holds, we can also assume
$1 \vee 2 \vee 3 \vee 4 \vee 5$
holds, we can also assume
![]() $\neg 1 \land \neg 2 \land \neg 3 \land \neg 4 \land \neg 5$
. Then by Proposition 4.18 (in mixed characteristic) and Proposition 4.20 (in positive characteristic), there is a definable non-trivial henselian valuation on
$\neg 1 \land \neg 2 \land \neg 3 \land \neg 4 \land \neg 5$
. Then by Proposition 4.18 (in mixed characteristic) and Proposition 4.20 (in positive characteristic), there is a definable non-trivial henselian valuation on
![]() $K$
.
$K$
.
6 Examples and questions
We isolate a few interesting examples where our result yields the existence of non-trivial definable henselian valuations. We then discuss the difficulties in building ones satisfying certain properties. We refer to the six conditions in the Main Theorem as conditions
![]() $1$
,
$1$
,
![]() $2$
,
$2$
,
![]() $3$
,
$3$
,
![]() $4$
,
$4$
,
![]() $5$
, and
$5$
, and
![]() $6$
, and to their negations as conditions
$6$
, and to their negations as conditions
![]() $\neg 1$
,
$\neg 1$
,
![]() $\neg 2$
,
$\neg 2$
,
![]() $\neg 3$
,
$\neg 3$
,
![]() $\neg 4$
,
$\neg 4$
,
![]() $\neg 5$
, and
$\neg 5$
, and
![]() $\neg 6$
.
$\neg 6$
.
We start with the following observation.
Remark 6.1. Let
![]() $(K,v)$
be a henselian valued field with
$(K,v)$
be a henselian valued field with
![]() $Kv$
non-henselian and not separably closed. Then
$Kv$
non-henselian and not separably closed. Then
![]() $v=v_K$
is the canonical henselian valuation on
$v=v_K$
is the canonical henselian valuation on
![]() $K$
. Indeed, there can be no proper henselian refinements of
$K$
. Indeed, there can be no proper henselian refinements of
![]() $v$
, as they would correspond to non-trivial henselian valuations on
$v$
, as they would correspond to non-trivial henselian valuations on
![]() $Kv$
via 2.1. Thus
$Kv$
via 2.1. Thus
![]() $H_2(K)$
is empty and
$H_2(K)$
is empty and
![]() $v$
is the finest valuation in
$v$
is the finest valuation in
![]() $H_1(K)$
.
$H_1(K)$
.
The aim of this section is to give some examples for fields where our Main Theorem yields a definable non-trivial henselian valuation because of conditions
![]() $5$
or
$5$
or
![]() $6$
(while at the same time
$6$
(while at the same time
![]() $\neg 1\wedge \neg 2\wedge \neg 3\wedge \neg 4$
holds). This boils down to finding a non-henselian t-henselian field that is not separably closed and such that we can control some properties of the canonical henselian valuation in some elementary extension (to access conditions
$\neg 1\wedge \neg 2\wedge \neg 3\wedge \neg 4$
holds). This boils down to finding a non-henselian t-henselian field that is not separably closed and such that we can control some properties of the canonical henselian valuation in some elementary extension (to access conditions
![]() $3$
and
$3$
and
![]() $6$
).
$6$
).
The construction of non-henselian t-henselian fields goes back to Prestel and Ziegler, see [Reference Prestel and Ziegler19, p. 338]. Other instances can be found in [Reference Fehm and Jahnke5, Proposition 6.7] (note that the field constructed there is elementary equivalent to a field admitting a non-trivial henselian valuation with divisible value group) and in [Reference Jahnke and Koenigsmann10, Examples 3.8 and 5.4] (with an elementary extension
![]() $L$
such that
$L$
such that
![]() $v_LL$
is not divisible). All of these provide fields of characteristic
$v_LL$
is not divisible). All of these provide fields of characteristic
![]() $0$
. In [Reference Anscombe and Jahnke1, Proposition 4.13], there is a construction of a non-henselian t-henselian field of positive characteristic that is elementary equivalent to a field admitting a non-trivial tame valuation with divisible value group. Such a field will serve as the residue field of the canonical henselian valuation to construct examples that satisfy condition
$0$
. In [Reference Anscombe and Jahnke1, Proposition 4.13], there is a construction of a non-henselian t-henselian field of positive characteristic that is elementary equivalent to a field admitting a non-trivial tame valuation with divisible value group. Such a field will serve as the residue field of the canonical henselian valuation to construct examples that satisfy condition
![]() $5$
, see Example 6.8. We will also adapt their construction in Lemma 6.13 and Proposition 6.14 to serve as the residue field of the canonical henselian valuation of an example that satisfies condition
$5$
, see Example 6.8. We will also adapt their construction in Lemma 6.13 and Proposition 6.14 to serve as the residue field of the canonical henselian valuation of an example that satisfies condition
![]() $6$
.
$6$
.
The following is needed to check that the constructed examples satisfy condition
![]() $\neg 3$
.
$\neg 3$
.
Proposition 6.2. Let
![]() $K$
be non-henselian and t-henselian such that there is
$K$
be non-henselian and t-henselian such that there is
![]() $K^*\equiv K$
admitting a non-trivial henselian valuation
$K^*\equiv K$
admitting a non-trivial henselian valuation
![]() $v^*$
with divisible value group. Then for all
$v^*$
with divisible value group. Then for all
![]() $L\equiv K$
,
$L\equiv K$
,
![]() $v_LL$
is divisible.
$v_LL$
is divisible.
Proof. We may assume that
![]() $L$
is henselian and not separably closed. Otherwise
$L$
is henselian and not separably closed. Otherwise
![]() $v_L$
is trivial and
$v_L$
is trivial and
![]() $v_LL$
is the trivial group which is divisible. In particular,
$v_LL$
is the trivial group which is divisible. In particular,
![]() $K$
is not separably closed.
$K$
is not separably closed.
By the Keisler–Shelah isomorphism theorem [Reference Marker17, Theorem 2.5.36], there are an index set
![]() $I$
and an ultrafilter
$I$
and an ultrafilter
![]() $\mathcal U$
on
$\mathcal U$
on
![]() $I$
such that
$I$
such that ![]() . Let
. Let ![]() and
and ![]() .
.
We claim that
![]() $(v^*)^{\mathcal U}$
and
$(v^*)^{\mathcal U}$
and
![]() $(v_L)^{\mathcal U}$
are comparable. Suppose not: then,
$(v_L)^{\mathcal U}$
are comparable. Suppose not: then,
![]() $Lv_L$
is separably closed, and by Theorem 2.8(1)
$Lv_L$
is separably closed, and by Theorem 2.8(1)
![]() $L$
admits an
$L$
admits an
![]() $\varnothing $
-definable non-trivial henselian valuation. The same formula then defines an
$\varnothing $
-definable non-trivial henselian valuation. The same formula then defines an
![]() $\varnothing $
-definable non-trivial henselian valuation on
$\varnothing $
-definable non-trivial henselian valuation on
![]() $K$
, contradicting the fact that
$K$
, contradicting the fact that
![]() $K$
is non-henselian.
$K$
is non-henselian.
Now we have to treat two cases. First, if
![]() $(v_L)^{\mathcal U}$
is a coarsening of
$(v_L)^{\mathcal U}$
is a coarsening of
![]() $(v^*)^{\mathcal U}$
. Then
$(v^*)^{\mathcal U}$
. Then
![]() $(v_L)^{\mathcal U}F$
is a quotient of
$(v_L)^{\mathcal U}F$
is a quotient of
![]() $(v^*)^{\mathcal U}F$
modulo some convex subgroup. Since
$(v^*)^{\mathcal U}F$
modulo some convex subgroup. Since
![]() $v^*K^*$
is divisible by assumption, so is
$v^*K^*$
is divisible by assumption, so is
![]() $(v^*)^{\mathcal U}F=(v^*K^*)^{\mathcal U}$
, which then implies that also
$(v^*)^{\mathcal U}F=(v^*K^*)^{\mathcal U}$
, which then implies that also
![]() $(v_L)^{\mathcal {U}}F=(v_LL)^{\mathcal U}$
and
$(v_L)^{\mathcal {U}}F=(v_LL)^{\mathcal U}$
and
![]() $v_LL$
are divisible.
$v_LL$
are divisible.
Second, if
![]() $(v_L)^{\mathcal U}$
is a proper refinement of
$(v_L)^{\mathcal U}$
is a proper refinement of
![]() $(v^*)^{\mathcal U}$
, then
$(v^*)^{\mathcal U}$
, then
![]() $(v^*)^{\mathcal U}F$
is a non-trivial quotient of
$(v^*)^{\mathcal U}F$
is a non-trivial quotient of
![]() $(v_L)^{\mathcal U}F$
. We assume for a contradiction that
$(v_L)^{\mathcal U}F$
. We assume for a contradiction that
![]() $(v_L)^{\mathcal U}F$
is not
$(v_L)^{\mathcal U}F$
is not
![]() $p$
-divisible for some prime
$p$
-divisible for some prime
![]() $p$
. Now,
$p$
. Now,
![]() $(v_L)^{\mathcal U}F$
is also not
$(v_L)^{\mathcal U}F$
is also not
![]() $p$
-antiregular, since
$p$
-antiregular, since
![]() $(v^*)^{\mathcal U}F$
is a non-trivial quotient, which is divisible. Thus, by Theorem 2.8(3),
$(v^*)^{\mathcal U}F$
is a non-trivial quotient, which is divisible. Thus, by Theorem 2.8(3),
![]() $L$
and thus also
$L$
and thus also
![]() $K$
admit
$K$
admit
![]() $\varnothing $
-definable non-trivial henselian valuations, but
$\varnothing $
-definable non-trivial henselian valuations, but
![]() $K$
is non-henselian, a contradiction. Hence
$K$
is non-henselian, a contradiction. Hence
![]() $(v_L)^{\mathcal U}F=(v_LL)^{\mathcal U}$
is divisible and so is
$(v_L)^{\mathcal U}F=(v_LL)^{\mathcal U}$
is divisible and so is
![]() $v_LL$
.
$v_LL$
.
Remark 6.3. In the following, we will construct examples where
![]() $K$
has positive characteristic. It would be interesting to also produce examples in mixed characteristic. This essentially would amount to finding a way to construct a valued field
$K$
has positive characteristic. It would be interesting to also produce examples in mixed characteristic. This essentially would amount to finding a way to construct a valued field
![]() $(K,v)$
of mixed characteristic, such that
$(K,v)$
of mixed characteristic, such that
![]() $vK$
is divisible,
$vK$
is divisible,
![]() $\mathcal {O}_{v}/p$
is semi-perfect, and
$\mathcal {O}_{v}/p$
is semi-perfect, and
![]() $Kv$
is some prescribed residue field. We are not aware of such a construction.
$Kv$
is some prescribed residue field. We are not aware of such a construction.
6.1 Puiseux series
We use the Puiseux series construction to build an example of a field satisfying conditions
![]() $\neg 1 \land \neg 2 \land \neg 3\land \neg 4 \land 5$
of the Main Theorem.
$\neg 1 \land \neg 2 \land \neg 3\land \neg 4 \land 5$
of the Main Theorem.
Definition 6.4 [Reference Anscombe and Jahnke1, Definition 4.4].
A field
![]() $K$
is of divisible-tame type if there exist
$K$
is of divisible-tame type if there exist
![]() $L \equiv K$
and a non-trivial valuation
$L \equiv K$
and a non-trivial valuation
![]() $w$
on
$w$
on
![]() $L$
such that
$L$
such that
![]() $(L,w)$
is tame with
$(L,w)$
is tame with
![]() $wL$
divisible.
$wL$
divisible.
Remark 6.5. In particular, every divisible-tame type field is perfect.
Fact 6.6 [Reference Anscombe and Jahnke1, Proposition 4.13].
Let
![]() $p$
be a prime or zero. There exists a non-henselian t-henselian field of characteristic
$p$
be a prime or zero. There exists a non-henselian t-henselian field of characteristic
![]() $p$
which is:
$p$
which is:
-
(1) not separably closed, and
-
(2) of divisible-tame type.
We will use the following folklore fact, whose proof we sketch out as we could not find a reference in the literature.
Lemma 6.7. Let
![]() $K_0$
be a field of characteristic
$K_0$
be a field of characteristic
![]() $p>0$
. Consider the Puiseux series over
$p>0$
. Consider the Puiseux series over
![]() $K_0$
,
$K_0$
,

together with the restriction
![]() $v_t$
of the
$v_t$
of the
![]() $t$
-adic valuation from
$t$
-adic valuation from
![]() $K_0(\!(\mathbb {Q})\!)$
. Then,
$K_0(\!(\mathbb {Q})\!)$
. Then,
![]() $(K,v_t)$
is a henselian valued field of positive characteristic,
$(K,v_t)$
is a henselian valued field of positive characteristic,
![]() $v_t$
is not defectless, and if
$v_t$
is not defectless, and if
![]() $K_0$
is perfect, then so is
$K_0$
is perfect, then so is
![]() $K$
.
$K$
.
Proof. As
![]() $(K,v_t)$
is the increasing union of henselian fields,
$(K,v_t)$
is the increasing union of henselian fields,
![]() $v_t$
is henselian. However, it is not algebraically maximal. Indeed, the equation
$v_t$
is henselian. However, it is not algebraically maximal. Indeed, the equation
![]() $X^p-X-\frac {1}{t} = 0$
has no solution in
$X^p-X-\frac {1}{t} = 0$
has no solution in
![]() $K$
, however it admits a solution in
$K$
, however it admits a solution in
![]() $K_0(\!(\mathbb Q)\!)$
, namely
$K_0(\!(\mathbb Q)\!)$
, namely
![]() $a = \sum _{n \geq 0} t^{-\frac {1}{p^n}}$
. Then,
$a = \sum _{n \geq 0} t^{-\frac {1}{p^n}}$
. Then,
![]() $K \subsetneq K(a) \subseteq K_0(\!(\mathbb {Q})\!)$
is a tower of immediate extensions, thus
$K \subsetneq K(a) \subseteq K_0(\!(\mathbb {Q})\!)$
is a tower of immediate extensions, thus
![]() $K \subsetneq K(a)$
is a proper algebraic immediate extension. Note that if
$K \subsetneq K(a)$
is a proper algebraic immediate extension. Note that if
![]() $K_0$
is perfect, then
$K_0$
is perfect, then
![]() $K_0(\!(t^{\frac {1}{n}})\!)^{\frac {1}{p}} = K_0(\!(t^{\frac {1}{np}})\!)$
for every
$K_0(\!(t^{\frac {1}{n}})\!)^{\frac {1}{p}} = K_0(\!(t^{\frac {1}{np}})\!)$
for every
![]() $n$
, and thus the union
$n$
, and thus the union
![]() $K$
is perfect.
$K$
is perfect.
Example 6.8. Let
![]() $K_0$
be a non-henselian t-henselian field of characteristic
$K_0$
be a non-henselian t-henselian field of characteristic
![]() $p>0$
which is not separably closed, and such that there exist
$p>0$
which is not separably closed, and such that there exist
![]() $L \equiv K_0$
and a non-trivial henselian valuation
$L \equiv K_0$
and a non-trivial henselian valuation
![]() $w$
on
$w$
on
![]() $L$
such that
$L$
such that
![]() $wL$
is divisible (such a
$wL$
is divisible (such a
![]() $K_0$
exists, for example, by Fact 6.6). Then,
$K_0$
exists, for example, by Fact 6.6). Then,

satisfies
![]() $\neg 1 \land \neg 2 \land \neg 3\land \neg 4 \land 5$
from our Main Theorem. Indeed, we have
$\neg 1 \land \neg 2 \land \neg 3\land \neg 4 \land 5$
from our Main Theorem. Indeed, we have
![]() $v_K=v_t$
by Remark 6.1. Now conditions
$v_K=v_t$
by Remark 6.1. Now conditions
![]() $\neg 1$
,
$\neg 1$
,
![]() $\neg 2$
, and
$\neg 2$
, and
![]() $\neg 4$
are immediate from the construction, condition
$\neg 4$
are immediate from the construction, condition
![]() $\neg 3$
follows from Proposition 6.2 and condition
$\neg 3$
follows from Proposition 6.2 and condition
![]() $5$
holds because of Lemma 6.7. It then follows that
$5$
holds because of Lemma 6.7. It then follows that
![]() $K$
admits a definable non-trivial henselian valuation.
$K$
admits a definable non-trivial henselian valuation.
6.2 Condition
 $6$
is necessary
$6$
is necessary
We adapt a construction from [Reference Anscombe and Jahnke1] to produce non-henselian, t-henselian fields with defect in some elementary extension. We first introduce a series of weakenings of henselianity.
Definition 6.9 [Reference Anscombe and Jahnke1, Definition 3.3].
Let
![]() $n \geq 1$
. Say that a valued field
$n \geq 1$
. Say that a valued field
![]() $(K,v)$
is
$(K,v)$
is
![]() $n_{\leq }$
-henselian if for every
$n_{\leq }$
-henselian if for every
![]() $f \in \mathcal {O}_v[X]$
of degree
$f \in \mathcal {O}_v[X]$
of degree
![]() $\leq n$
, and
$\leq n$
, and
![]() $a \in \mathcal {O}_v$
, if
$a \in \mathcal {O}_v$
, if
![]() $v(f(a))> 0$
and
$v(f(a))> 0$
and
![]() $v(f'(a)) = 0$
, then there is
$v(f'(a)) = 0$
, then there is
![]() $b \in \mathcal {O}_v$
with
$b \in \mathcal {O}_v$
with
![]() $f(b) = 0$
and
$f(b) = 0$
and
![]() $v(b-a)> 0$
.
$v(b-a)> 0$
.
Definition 6.10 [Reference Engler and Prestel4, Section 4.2].
Let
![]() $q$
be a prime. Say that a valued field
$q$
be a prime. Say that a valued field
![]() $(K,v)$
is q-henselian if
$(K,v)$
is q-henselian if
![]() $v$
extends uniquely to every Galois extension of
$v$
extends uniquely to every Galois extension of
![]() $K$
of
$K$
of
![]() $q$
-power degree.
$q$
-power degree.
Remark 6.11. A valued field
![]() $(K,v)$
is henselian if and only if it is
$(K,v)$
is henselian if and only if it is
![]() $n_\leq $
-henselian for all
$n_\leq $
-henselian for all
![]() $n$
. Being
$n$
. Being
![]() $n_\leq $
-henselian is clearly a first-order property of
$n_\leq $
-henselian is clearly a first-order property of
![]() $(K,v)$
; by [Reference Koenigsmann13, Propositions 1.2 and 1.3], the same is true for
$(K,v)$
; by [Reference Koenigsmann13, Propositions 1.2 and 1.3], the same is true for
![]() $q$
-henselianity.
$q$
-henselianity.
Next, we isolate a new notion built along the lines of t-henselianity and divisible-tame type.
Definition 6.12. We call a field K t-henselian of defect type if there is an elementarily equivalent
![]() $L \equiv K$
which admits some henselian valuation
$L \equiv K$
which admits some henselian valuation
![]() $v$
such that
$v$
such that
![]() $(L,v)$
has defect. We call a field K t-henselian of divisible-defect type if there is an elementarily equivalent
$(L,v)$
has defect. We call a field K t-henselian of divisible-defect type if there is an elementarily equivalent
![]() $L \equiv K$
which admits some henselian valuation
$L \equiv K$
which admits some henselian valuation
![]() $v$
such that
$v$
such that
![]() $(L,v)$
has defect with
$(L,v)$
has defect with
![]() $vL$
divisible.
$vL$
divisible.
We now replicate a construction that first appeared in [Reference Prestel and Ziegler19], and was later refined in [Reference Fehm and Jahnke5] and [Reference Anscombe and Jahnke1]. The proofs are almost verbatim the same as in [Reference Fehm and Jahnke5] and [Reference Anscombe and Jahnke1]; we thus give the appropriate references and explain the differences.
Lemma 6.13 [Reference Anscombe and Jahnke1, Lemma 4.8].
Let
![]() $p> 0$
be a prime. Let
$p> 0$
be a prime. Let
![]() $K$
be a perfect field of characteristic
$K$
be a perfect field of characteristic
![]() $p$
that contains all roots of unity. Let
$p$
that contains all roots of unity. Let
![]() $n> p$
and let
$n> p$
and let
![]() $q$
be a prime with
$q$
be a prime with
![]() $q> n$
. Then, there exists an equicharacteristic valued field
$q> n$
. Then, there exists an equicharacteristic valued field
![]() $(K',v)$
with:
$(K',v)$
with:
-
•
 $K'v = K$
,
$K'v = K$
,
 $vK' = \mathbb Q$
,
$vK' = \mathbb Q$
, -
•
 $K'$
is perfect,
$K'$
is perfect, -
•
 $(K',v)$
is not
$(K',v)$
is not
 $q$
-henselian, but it is
$q$
-henselian, but it is
 $n_{\leq }$
-henselian,
$n_{\leq }$
-henselian, -
•
 $(K',v)$
admits a proper degree
$(K',v)$
admits a proper degree
 $p$
immediate extension.
$p$
immediate extension.
Proof. We follow the proof of [Reference Anscombe and Jahnke1, Lemma 4.8], but we substitute the generalized power series with the Puiseux series. Indeed, inside the Puiseux series ![]() , endowed with the restriction
, endowed with the restriction
![]() $v_t$
of the
$v_t$
of the
![]() $t$
-adic valuation on
$t$
-adic valuation on
![]() $K(\!(\mathbb Q)\!)$
, consider the subfield
$K(\!(\mathbb Q)\!)$
, consider the subfield ![]() . Consider
. Consider ![]() . Note that since
. Note that since
![]() $L$
is henselian, so is
$L$
is henselian, so is
![]() $\widetilde {F}$
. Then, arguing as in [Reference Anscombe and Jahnke1, proof of Lemma 4.8], there is a subgroup
$\widetilde {F}$
. Then, arguing as in [Reference Anscombe and Jahnke1, proof of Lemma 4.8], there is a subgroup
![]() $G \leq {\operatorname {Gal}({F^{\mathrm {sep}}} | {F})}$
with
$G \leq {\operatorname {Gal}({F^{\mathrm {sep}}} | {F})}$
with
![]() $G \cong \mathbb Z_q$
.
$G \cong \mathbb Z_q$
.
Let
![]() $E = \operatorname {Fix}(G) \subseteq F^{\mathrm {sep}}$
, and consider
$E = \operatorname {Fix}(G) \subseteq F^{\mathrm {sep}}$
, and consider ![]() . Then,
. Then,
![]() $(K',v_t)$
has residue field
$(K',v_t)$
has residue field
![]() $K$
and value group
$K$
and value group
![]() $\mathbb Q$
, and it is perfect. Moreover, the roots of
$\mathbb Q$
, and it is perfect. Moreover, the roots of
![]() $X^p-X-\frac {1}{t}$
give rise to immediate extensions of degree
$X^p-X-\frac {1}{t}$
give rise to immediate extensions of degree
![]() $p$
over
$p$
over
![]() $(K',v_t)$
. Now, arguing as in [Reference Anscombe and Jahnke1, Claim 4.8.1],
$(K',v_t)$
. Now, arguing as in [Reference Anscombe and Jahnke1, Claim 4.8.1],
![]() $(K',v_t)$
is not
$(K',v_t)$
is not
![]() $q$
-henselian. Similarly, arguing as in [Reference Anscombe and Jahnke1, Claim 4.8.2],
$q$
-henselian. Similarly, arguing as in [Reference Anscombe and Jahnke1, Claim 4.8.2],
![]() $(K',v_t)$
is
$(K',v_t)$
is
![]() $n_{\leq }$
-henselian (note that they argue that
$n_{\leq }$
-henselian (note that they argue that
![]() $(K',v_t)$
is
$(K',v_t)$
is
![]() $(n!^2!)_{\leq }$
-henselian, using that in their case
$(n!^2!)_{\leq }$
-henselian, using that in their case
![]() $q> n!^2!$
).
$q> n!^2!$
).
As for the last point, note that
![]() $L$
admits an immediate extension of degree
$L$
admits an immediate extension of degree
![]() $p$
, namely given by any root of the Artin–Schreier polynomial
$p$
, namely given by any root of the Artin–Schreier polynomial
![]() $X^p-X-\frac {1}{t}$
. In particular, then,
$X^p-X-\frac {1}{t}$
. In particular, then,
![]() $\widetilde {F}$
also admits an immediate extension of degree
$\widetilde {F}$
also admits an immediate extension of degree
![]() $p$
, and thus so does
$p$
, and thus so does
![]() $K'$
.
$K'$
.
The following construction follows very closely the proof of [Reference Anscombe and Jahnke1, Proposition 4.13], using Lemma 6.13 in place of [Reference Anscombe and Jahnke1, Lemma 4.8] and diverging only in the last paragraph. We sketch out the construction for the convenience of the reader, but invite them to see [Reference Anscombe and Jahnke1] and [Reference Fehm and Jahnke5] for the full details.
Proposition 6.14 [Reference Anscombe and Jahnke1, Proposition 4.13].
Let
![]() $p> 0$
be a prime. There is a non-henselian, t-henselian of divisible-defect type perfect field of characteristic
$p> 0$
be a prime. There is a non-henselian, t-henselian of divisible-defect type perfect field of characteristic
![]() $p$
which is not separably closed.
$p$
which is not separably closed.
Proof. For each
![]() $n \geq 0$
, set
$n \geq 0$
, set
![]() $k_n = n+p+1$
and choose a prime
$k_n = n+p+1$
and choose a prime
![]() $q_n> k_n$
. Let
$q_n> k_n$
. Let
![]() $K_0 = \mathbb F_p^{\mathrm {alg}}$
. Then, using Lemma 6.13, build a sequence
$K_0 = \mathbb F_p^{\mathrm {alg}}$
. Then, using Lemma 6.13, build a sequence
![]() $\{(K_{n+1},\overline {v_n}) \mid n \geq 0\}$
of valued fields such that each
$\{(K_{n+1},\overline {v_n}) \mid n \geq 0\}$
of valued fields such that each
![]() $(K_{n+1},\overline {v_{n}})$
has value group
$(K_{n+1},\overline {v_{n}})$
has value group
![]() $\mathbb Q$
, residue field
$\mathbb Q$
, residue field
![]() $K_{n}$
, is not
$K_{n}$
, is not
![]() $q_n$
-henselian, but it is
$q_n$
-henselian, but it is
![]() ${(k_n)}_{\leq }$
-henselian, and it admits a proper degree
${(k_n)}_{\leq }$
-henselian, and it admits a proper degree
![]() $p$
immediate extension.
$p$
immediate extension.
For any
![]() $n> m \geq 0$
, then, write
$n> m \geq 0$
, then, write ![]() and denote by
and denote by
![]() $\mathcal {O}_{n,m}$
the corresponding valuation ring on
$\mathcal {O}_{n,m}$
the corresponding valuation ring on
![]() $K_n$
. Denote by
$K_n$
. Denote by
![]() $\pi _{n,m} \colon \mathcal {O}_{n,0} \to \mathcal {O}_{m,0}$
the restriction of the residue map
$\pi _{n,m} \colon \mathcal {O}_{n,0} \to \mathcal {O}_{m,0}$
the restriction of the residue map
![]() $\mathcal {O}_{n,m} \to K_m$
. Then, the valuation rings
$\mathcal {O}_{n,m} \to K_m$
. Then, the valuation rings
![]() $(\mathcal {O}_{n,0})_{n \geq 0}$
form a projective system together with the maps
$(\mathcal {O}_{n,0})_{n \geq 0}$
form a projective system together with the maps
![]() $\pi _{n,m}$
. The limit
$\pi _{n,m}$
. The limit
![]() $\mathcal {O}$
is again a valuation ring, together with natural projections
$\mathcal {O}$
is again a valuation ring, together with natural projections
![]() $\pi _{\infty ,n} \colon \mathcal {O} \to \mathcal {O}_{n,0}$
. For each
$\pi _{\infty ,n} \colon \mathcal {O} \to \mathcal {O}_{n,0}$
. For each
![]() $n \geq 0$
, consider the localization
$n \geq 0$
, consider the localization ![]() . Each
. Each
![]() $\mathcal {O}_{v_n}$
is a valuation ring on
$\mathcal {O}_{v_n}$
is a valuation ring on
![]() $K = \operatorname {Frac}(\mathcal {O}) = \bigcup _{n \geq 0} \mathcal {O}_{v_n}$
with residue field
$K = \operatorname {Frac}(\mathcal {O}) = \bigcup _{n \geq 0} \mathcal {O}_{v_n}$
with residue field
![]() $K_n$
and non-trivial divisible value group. Indeed, for each
$K_n$
and non-trivial divisible value group. Indeed, for each
![]() $n \geq 0$
,
$n \geq 0$
,
![]() $\mathcal {O}_{v_n} \subseteq \mathcal {O}_{v_{n+1}}$
, and
$\mathcal {O}_{v_n} \subseteq \mathcal {O}_{v_{n+1}}$
, and
![]() $v_{n}$
induces precisely
$v_{n}$
induces precisely
![]() $\overline {v_n}$
on
$\overline {v_n}$
on
![]() $K_{n+1} = Kv_{n+1}$
.
$K_{n+1} = Kv_{n+1}$
.

We now let
![]() $(K^*,v^*)$
be an ultraproduct of the family
$(K^*,v^*)$
be an ultraproduct of the family
![]() $(K,v_n)_{n \geq 0}$
. Then,
$(K,v_n)_{n \geq 0}$
. Then,
![]() $K^*$
is perfect, and
$K^*$
is perfect, and
![]() $v^*$
is henselian with divisible value group. Moreover,
$v^*$
is henselian with divisible value group. Moreover,
![]() $K$
is not henselian and thus not separably closed.
$K$
is not henselian and thus not separably closed.
Now, we diverge from the proof of [Reference Anscombe and Jahnke1, Proposition 4.13] and argue that
![]() $(K^*,v^*)$
admits a degree
$(K^*,v^*)$
admits a degree
![]() $p$
immediate extension, in particular a defect extension. It is enough to show that each
$p$
immediate extension, in particular a defect extension. It is enough to show that each
![]() $(K,v_n)$
admits one such. We know that
$(K,v_n)$
admits one such. We know that
![]() $(K_{n+1},\overline {v_n})$
admits a degree
$(K_{n+1},\overline {v_n})$
admits a degree
![]() $p$
immediate extension generated by a root
$p$
immediate extension generated by a root
![]() $\alpha $
of an Artin–Schreier polynomial
$\alpha $
of an Artin–Schreier polynomial
![]() $X^p-X-\xi $
, for some
$X^p-X-\xi $
, for some
![]() $\xi \in K_{n+1}$
. Denote by
$\xi \in K_{n+1}$
. Denote by
![]() $\overline {u}$
the prolongation of
$\overline {u}$
the prolongation of
![]() $\overline {v_n}$
to
$\overline {v_n}$
to
![]() $K_{n+1}(\alpha )$
that makes
$K_{n+1}(\alpha )$
that makes
![]() $(K_{n+1}(\alpha ),\overline {u})$
immediate over
$(K_{n+1}(\alpha ),\overline {u})$
immediate over
![]() $(K_{n+1},\overline {v_n})$
. For some
$(K_{n+1},\overline {v_n})$
. For some
![]() $z \in K$
with
$z \in K$
with
![]() $\operatorname {\mathrm {res}}_{v_{n+1}}(z) = \xi $
, we consider the Artin–Schreier polynomial
$\operatorname {\mathrm {res}}_{v_{n+1}}(z) = \xi $
, we consider the Artin–Schreier polynomial
![]() $X^p-X-z$
. Let
$X^p-X-z$
. Let
![]() $w$
be a prolongation of
$w$
be a prolongation of
![]() $v_{n+1}$
to
$v_{n+1}$
to
![]() $K^{\mathrm {alg}}$
: then there is
$K^{\mathrm {alg}}$
: then there is
![]() $a \in K^{\mathrm {alg}}$
with
$a \in K^{\mathrm {alg}}$
with
![]() $a^p-a-z = 0$
and
$a^p-a-z = 0$
and
![]() $\operatorname {\mathrm {res}}_{w}(a) = \alpha $
, by henselianity of
$\operatorname {\mathrm {res}}_{w}(a) = \alpha $
, by henselianity of
![]() $w$
. Then, if we denote by
$w$
. Then, if we denote by
![]() $w$
again the restriction of
$w$
again the restriction of
![]() $w$
to
$w$
to
![]() $K(a)$
, we have that
$K(a)$
, we have that
![]() $K(a)w = Kw(\alpha ) = K_{n+1}(\alpha )$
. We now let
$K(a)w = Kw(\alpha ) = K_{n+1}(\alpha )$
. We now let
![]() $u = \overline {u} \circ w$
. Then,
$u = \overline {u} \circ w$
. Then,
![]() $K(a)u = K_{n+1}(\alpha )\overline {u} = Kv_n$
. Moreover,
$K(a)u = K_{n+1}(\alpha )\overline {u} = Kv_n$
. Moreover,
![]() $v_nK$
is divisible, so
$v_nK$
is divisible, so
![]() $uK(a) = v_nK$
.
$uK(a) = v_nK$
.
Proposition 6.15. Let
![]() $K$
be a non-henselian, t-henselian of defect type, perfect field of characteristic
$K$
be a non-henselian, t-henselian of defect type, perfect field of characteristic
![]() $p$
which is not separably closed. Let
$p$
which is not separably closed. Let
![]() $L \equiv K$
be such that, for some henselian valuation
$L \equiv K$
be such that, for some henselian valuation
![]() $v$
,
$v$
,
![]() $(L,v)$
has defect. Then
$(L,v)$
has defect. Then
![]() $v_L$
has defect.
$v_L$
has defect.
Proof. We distinguish two cases. If
![]() $v$
is a (possibly non-proper) coarsening of
$v$
is a (possibly non-proper) coarsening of
![]() $v_L$
, then we are done, since defect goes up in coarsenings. If
$v_L$
, then we are done, since defect goes up in coarsenings. If
![]() $v$
is a proper refinement of
$v$
is a proper refinement of
![]() $v_L$
, then
$v_L$
, then
![]() $Lv_L$
is separably closed, and since
$Lv_L$
is separably closed, and since
![]() $L$
is perfect, it is in particular algebraically closed. Thus, the valuation
$L$
is perfect, it is in particular algebraically closed. Thus, the valuation
![]() $\overline {v}$
induced by
$\overline {v}$
induced by
![]() $v$
on
$v$
on
![]() $Lv_L$
is defectless. But then, since
$Lv_L$
is defectless. But then, since
![]() $v = \overline {v} \circ v_L$
has defect if and only at least one of
$v = \overline {v} \circ v_L$
has defect if and only at least one of
![]() $v_L$
and
$v_L$
and
![]() $\overline {v}$
has defect [Reference Anscombe and Jahnke2, Lemma 2.9],
$\overline {v}$
has defect [Reference Anscombe and Jahnke2, Lemma 2.9],
![]() $v_L$
must have defect.
$v_L$
must have defect.
Remark 6.16. The construction in Proposition 6.14 shows that in equicharacteristic
![]() $p$
, one cannot eliminate the parameters from Corollary 4.14. Indeed, assume that, on any perfect henselian valued field
$p$
, one cannot eliminate the parameters from Corollary 4.14. Indeed, assume that, on any perfect henselian valued field
![]() $(F,v)$
of characteristic
$(F,v)$
of characteristic
![]() $p>0$
such that
$p>0$
such that
![]() $v$
is not defectless, there is a non-trivial
$v$
is not defectless, there is a non-trivial
![]() $\varnothing $
-definable henselian coarsening
$\varnothing $
-definable henselian coarsening
![]() $w$
of
$w$
of
![]() $v$
. Take a non-henselian, t-henselian of defect type, perfect field
$v$
. Take a non-henselian, t-henselian of defect type, perfect field
![]() $K$
(given by Proposition 6.14), and let
$K$
(given by Proposition 6.14), and let
![]() $L \equiv K$
be such that
$L \equiv K$
be such that
![]() $(L,v_L)$
has defect (which we can assume exists by Proposition 6.15). Then, there is a coarsening
$(L,v_L)$
has defect (which we can assume exists by Proposition 6.15). Then, there is a coarsening
![]() $w$
of
$w$
of
![]() $v_L$
which is
$v_L$
which is
![]() $\varnothing $
-definable. In particular, using the same formula, we can find a non-trivial henselian valuation on
$\varnothing $
-definable. In particular, using the same formula, we can find a non-trivial henselian valuation on
![]() $K$
, a contradiction.
$K$
, a contradiction.
Example 6.17. Let
![]() $p>0$
be a prime. Let
$p>0$
be a prime. Let
![]() $K_0$
be a non-henselian, t-henselian of divisible-defect type, perfect field of characteristic
$K_0$
be a non-henselian, t-henselian of divisible-defect type, perfect field of characteristic
![]() $p$
which is not separably closed. Then,
$p$
which is not separably closed. Then,
satisfies
![]() $\neg 1 \land \neg 2 \land \neg 3 \land \neg 4 \land \neg 5 \land 6$
from our Main Theorem. Indeed, we have
$\neg 1 \land \neg 2 \land \neg 3 \land \neg 4 \land \neg 5 \land 6$
from our Main Theorem. Indeed, we have
![]() $v_K=v_t$
by Remark 6.1. Now conditions
$v_K=v_t$
by Remark 6.1. Now conditions
![]() $\neg 1$
,
$\neg 1$
,
![]() $\neg 2$
,
$\neg 2$
,
![]() $\neg 4$
,
$\neg 4$
,
![]() $6$
are immediate from the construction,
$6$
are immediate from the construction,
![]() $\neg 5$
follows since
$\neg 5$
follows since
![]() $(K_0(\!(\mathbb Q)\!),v_t)$
is tame, and condition
$(K_0(\!(\mathbb Q)\!),v_t)$
is tame, and condition
![]() $\neg 3$
follows from Proposition 6.2. It then follows that
$\neg 3$
follows from Proposition 6.2. It then follows that
![]() $K$
admits a definable non-trivial henselian valuation.
$K$
admits a definable non-trivial henselian valuation.
Question 6.18. Let
![]() $K$
be a non-henselian, t-henselian of divisible-tame type field of characteristic
$K$
be a non-henselian, t-henselian of divisible-tame type field of characteristic
![]() $p$
which is not separably closed. Suppose that
$p$
which is not separably closed. Suppose that
![]() $L \equiv K$
admits a non-trivial henselian valuation. Must
$L \equiv K$
admits a non-trivial henselian valuation. Must
![]() $(L,v_L)$
be defectless? This is the defectless version of Proposition 6.2, and it would yield that if
$(L,v_L)$
be defectless? This is the defectless version of Proposition 6.2, and it would yield that if
![]() $K_0$
is non-henselian, t-henselian of divisible-tame type, not separably closed, then
$K_0$
is non-henselian, t-henselian of divisible-tame type, not separably closed, then
![]() $K_0(\!(\mathbb Q)\!)$
is an example for
$K_0(\!(\mathbb Q)\!)$
is an example for
![]() $\neg 1 \land \neg 2 \land \neg 3 \land \neg 4 \land \neg 5 \land \neg 6$
(and thus admits no non-trivial definable henselian valuation).
$\neg 1 \land \neg 2 \land \neg 3 \land \neg 4 \land \neg 5 \land \neg 6$
(and thus admits no non-trivial definable henselian valuation).
Acknowledgements
This work was done as part of the Ph.D. projects of the authors: we therefore wish to thank Sylvy Anscombe, Arno Fehm, Martin Hils, and Franziska Jahnke for their perfect guidance, highly valued encouragement, and dedication in finding and overcoming the defects in our arguments. We would like to express special thanks to S. Anscombe for pointing us towards Beth definability in time of need, to F. Jahnke for directing us towards and through these questions, and suggesting the use of independent defect, and to A. Fehm for pointing out how the proof of Proposition 3.6 could be simplified and applied in a more general setting. We also wish to thank Blaise Boissonneau, Nicolas Daans, Akash Hossain, and Franz-Viktor Kuhlmann for fruitful discussions. We thank the anonymous reviewer for the useful comments, that in particular led to the addition of Section 6.
This project began when the third author was a Visiting Doctoral Researcher to the Cluster of Excellence “Mathematics Münster”. Our thanks go to “Mathematics Münster” for providing a lively research environment where this project could start.
Funding
This research is supported by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under the Excellence Strategy EXC 2044-390685587, Mathematics Münster: Dynamics-Geometry-Structure. The first two authors are also supported by the German Research Foundation (DFG) via HI 2004/1-1 (part of the French-German ANR-DFG project GeoMod). The second author is also funded by the DFG project 495759320—Modelltheorie bewerteter Körper mit Endomorphismus. The third author is also funded by the DFG project 404427454—Definierbarkeit und Entscheidbarkeit in globalen und lokalen Körpern.