Published online by Cambridge University Press: 12 March 2014
The problem of coding relations by means of a single binary relation is well known in the mathematical literature. It was considered in interpretation theory, and also in connection with investigations of decidability of elementary theories. Using various constructions (see, e.g., [2,6], proofs of Theorem 11 in [7] and Theorem 16.51 in [3]), for any model 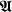 for a countable language, one can construct a model
for a countable language, one can construct a model 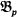 for ℒp (a language with a single binary relation symbol
for ℒp (a language with a single binary relation symbol 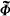 ) in which
) in which 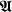 is interpretable. Each of the mentioned constructions has the same weak point: the universe of
is interpretable. Each of the mentioned constructions has the same weak point: the universe of 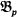 is different than the universe of
is different than the universe of 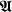 . In [4] we have shown that, in the infinite case, one can eliminate this defect, i.e., for any infinite
. In [4] we have shown that, in the infinite case, one can eliminate this defect, i.e., for any infinite 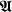 , we have constructed a model
, we have constructed a model 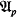 , having the same universe as
, having the same universe as 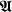 , in which
, in which 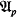 is elementarily definable. In all constructions mentioned above, it appears that formulas, which define
is elementarily definable. In all constructions mentioned above, it appears that formulas, which define 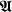 in
in 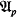 (
(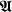 in
in 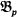 ), are very complicated. In the present paper, another construction of a model for ℒp is given.
), are very complicated. In the present paper, another construction of a model for ℒp is given.