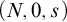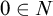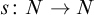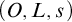1 Introduction
The introduction and study of ordinal numbers goes back to the pioneering works of Cantor in set theory [Reference Cantor2, Reference Cantor3]. In modern language, Cantor’s ordinal numbers are isomorphic classes of well-ordered sets, see e.g. [Reference Fraenkel5]. There is also a ‘concrete’ definition of an ordinal number as a transitive set which is well-ordered under the element relation—see e.g. [Reference Jech7]. Such sets are usually called von Neumann ordinals. Natural numbers can be seen concretely as the finite ordinal numbers. In Dedekind’s approach to the natural number system described in [Reference Dedekind4], the natural numbers are not defined as concrete objects, but rather as abstract entities organized in a certain structure; namely, a triple
![]() $(N,0,s)$
consisting of a set N (a set of ‘abstract’ natural numbers), a distinguished element
$(N,0,s)$
consisting of a set N (a set of ‘abstract’ natural numbers), a distinguished element
![]() $0$
of N (in [Reference Dedekind4], the distinguished element is 1), and a function
$0$
of N (in [Reference Dedekind4], the distinguished element is 1), and a function
![]() $s\colon N\to N$
, which names the ‘successor’ of each natural number. The axioms that such a system should satisfy were formulated by Dedekind, but are often referred to as Peano axioms today (see e.g. [Reference Wang16] for some historical background):
$s\colon N\to N$
, which names the ‘successor’ of each natural number. The axioms that such a system should satisfy were formulated by Dedekind, but are often referred to as Peano axioms today (see e.g. [Reference Wang16] for some historical background):
-
•
 $0$
does not belong to the image of s.
$0$
does not belong to the image of s. -
• s is injective.
-
•
 $X=N$
for any subset X of N that is closed under s and contains
$X=N$
for any subset X of N that is closed under s and contains
 $0$
.
$0$
.
It is an observation due to Lawvere [Reference Lawvere10] that these axioms identify the natural number systems as initial objects in the category of all triples
![]() $(X,x,t)$
where X is a set,
$(X,x,t)$
where X is a set,
![]() $x\in X$
and t is a function
$x\in X$
and t is a function
![]() $t\colon X\to X$
. This ‘universal property’ of the natural number system, freed from its category-theoretic formulation, is actually the ‘definition by induction’ theorem already contained in [Reference Dedekind4]. A morphism
$t\colon X\to X$
. This ‘universal property’ of the natural number system, freed from its category-theoretic formulation, is actually the ‘definition by induction’ theorem already contained in [Reference Dedekind4]. A morphism
![]() $(N,0,s)\to (X,x,t)$
of such triples is defined as a function
$(N,0,s)\to (X,x,t)$
of such triples is defined as a function
![]() $f\colon N\to X$
such that:
$f\colon N\to X$
such that:
-
•
 $f(0)=x,$
$f(0)=x,$
-
•
 $f(s(n))=t(f(n))$
for all
$f(s(n))=t(f(n))$
for all
 $n\in N$
.
$n\in N$
.
The ‘definition by induction’ theorem states that there is exactly one morphism to any other triple
![]() $(X,x,t)$
from the triple
$(X,x,t)$
from the triple
![]() $(N,0,s)$
satisfying the axioms stated above. This theorem is of course well known because of its practical use: it says that recursively defined functions exist and are uniquely determined by the recursion. Intuitively, the theorem can be understood as follows. A triple
$(N,0,s)$
satisfying the axioms stated above. This theorem is of course well known because of its practical use: it says that recursively defined functions exist and are uniquely determined by the recursion. Intuitively, the theorem can be understood as follows. A triple
![]() $(X,x,t)$
can be viewed as an abstraction of the concept of counting—X is the set of figures used in counting, x is where counting begins and the function t names increments when counting. Without further restrictions on such ‘counting systems’, there are many non-isomorphic ones, some of which are quite different from the natural number system, but still useful; for instance, hours on a clock, where counting loops back to
$(X,x,t)$
can be viewed as an abstraction of the concept of counting—X is the set of figures used in counting, x is where counting begins and the function t names increments when counting. Without further restrictions on such ‘counting systems’, there are many non-isomorphic ones, some of which are quite different from the natural number system, but still useful; for instance, hours on a clock, where counting loops back to
![]() $1$
once we pass
$1$
once we pass
![]() $12$
. A morphism of these triples can be viewed as a ‘translation’ of one counting system to another. The universal property of the natural number system presents it as a ‘universal’ counting system, in the sense that it has a unique translation to any other counting system. Incidentally, such intuition is not particular to the natural number system: many structures in mathematics can be defined by natural universal properties—see [Reference Mac Lane11].
$12$
. A morphism of these triples can be viewed as a ‘translation’ of one counting system to another. The universal property of the natural number system presents it as a ‘universal’ counting system, in the sense that it has a unique translation to any other counting system. Incidentally, such intuition is not particular to the natural number system: many structures in mathematics can be defined by natural universal properties—see [Reference Mac Lane11].
Ordinal numbers exhibit a similar structure to natural numbers—there is a ‘starting’ ordinal (the natural number
![]() $0$
), and every ordinal number has a successor. The natural numbers
$0$
), and every ordinal number has a successor. The natural numbers
![]() $0,1,2,3,\ldots $
are the first ordinal numbers. This set is closed under succession. The ordinal number system allows for another type of succession that can be applied to sets of ordinal numbers closed under succession, giving rise to the so-called ‘limit’ ordinal numbers. The infinite sequence of natural numbers is succeeded by a limit ordinal number, usually denoted by
$0,1,2,3,\ldots $
are the first ordinal numbers. This set is closed under succession. The ordinal number system allows for another type of succession that can be applied to sets of ordinal numbers closed under succession, giving rise to the so-called ‘limit’ ordinal numbers. The infinite sequence of natural numbers is succeeded by a limit ordinal number, usually denoted by
![]() $\omega $
. Now, we can take the ‘usual’ successor of
$\omega $
. Now, we can take the ‘usual’ successor of
![]() $\omega $
, call it
$\omega $
, call it
![]() $\omega +1$
, and keep taking its successors until we get another set that is closed under succession, after which we introduce another limit ordinal number—it will be
$\omega +1$
, and keep taking its successors until we get another set that is closed under succession, after which we introduce another limit ordinal number—it will be
![]() $\omega +\omega =\omega \cdot 2$
. The next limit ordinal number will be
$\omega +\omega =\omega \cdot 2$
. The next limit ordinal number will be
![]() $\omega \cdot 3$
. At some point, we reach
$\omega \cdot 3$
. At some point, we reach
![]() $\omega \cdot \omega =\omega ^2$
, then
$\omega \cdot \omega =\omega ^2$
, then
![]() $\omega ^3$
, and so on until we reach
$\omega ^3$
, and so on until we reach
![]() $\omega ^\omega $
, then
$\omega ^\omega $
, then
![]() $\omega ^\omega +1$
, and so on. The process is supposed to continue until all ordinal numbers that we have named no longer form a set. Let us also recall that von Neumann ordinals are defined as sets of preceding ordinals. Thus the first ordinal number, the number
$\omega ^\omega +1$
, and so on. The process is supposed to continue until all ordinal numbers that we have named no longer form a set. Let us also recall that von Neumann ordinals are defined as sets of preceding ordinals. Thus the first ordinal number, the number
![]() $0$
, is defined as
$0$
, is defined as
![]() $0=\varnothing $
and the successor of an ordinal number n is defined as
$0=\varnothing $
and the successor of an ordinal number n is defined as
![]() . A limit ordinal number is one that is the union of all preceding ordinal numbers. We can, in particular, think of
. A limit ordinal number is one that is the union of all preceding ordinal numbers. We can, in particular, think of
![]() $0$
as a limit ordinal number given by the union of its predecessors, since the empty union equals the empty set. Equivalently, limit ordinal numbers are those whose sets of predecessors are closed under succession.
$0$
as a limit ordinal number given by the union of its predecessors, since the empty union equals the empty set. Equivalently, limit ordinal numbers are those whose sets of predecessors are closed under succession.
We may also think of the ordinal number system in terms of a triple
![]() $(O,L,s)$
—this time, O is a class (since the collection of all ordinal numbers is no longer a set), L is a (class) function that specifies limit ordinals and is defined for those subclasses of O which form sets closed under the class function s, which specifies the successor of each ordinal. In this paper we show that the following three axioms on such a triple are suitable as analogues of the three Dedekind–Peano axioms for the ordinal number system:
$(O,L,s)$
—this time, O is a class (since the collection of all ordinal numbers is no longer a set), L is a (class) function that specifies limit ordinals and is defined for those subclasses of O which form sets closed under the class function s, which specifies the successor of each ordinal. In this paper we show that the following three axioms on such a triple are suitable as analogues of the three Dedekind–Peano axioms for the ordinal number system:
-
•
 $L(I{\kern-0.5pt})$
does not belong to the image of s, and also
$L(I{\kern-0.5pt})$
does not belong to the image of s, and also
 $s(L(I{\kern-0.5pt}))\notin I$
, for any I such that
$s(L(I{\kern-0.5pt}))\notin I$
, for any I such that
 $L(I{\kern-0.5pt})$
is defined.
$L(I{\kern-0.5pt})$
is defined. -
• s is injective and
 $L(I{\kern-0.5pt})=L(J{\kern-0.5pt})$
if and only if
$L(I{\kern-0.5pt})=L(J{\kern-0.5pt})$
if and only if
 $\overline {I}=\overline {J}$
and
$\overline {I}=\overline {J}$
and
 $L(I{\kern-0.5pt}),L(J{\kern-0.5pt})$
are defined, where
$L(I{\kern-0.5pt}),L(J{\kern-0.5pt})$
are defined, where
 $\overline {I}$
and
$\overline {I}$
and
 $\overline {J}$
denote closures of I and J, respectively, under s and L predecessors.
$\overline {J}$
denote closures of I and J, respectively, under s and L predecessors. -
•
 $X=O$
for any subclass X of O that is closed under s and that contains
$X=O$
for any subclass X of O that is closed under s and that contains
 $L(I{\kern-0.5pt})$
for each
$L(I{\kern-0.5pt})$
for each
 $I\subseteq X$
such that
$I\subseteq X$
such that
 $L(I{\kern-0.5pt})$
is defined.
$L(I{\kern-0.5pt})$
is defined.
In particular, we prove that:
-
• The system of von Neumann ordinals constitutes a triple
 $(O,L,s)$
satisfying the three axioms above. There is nothing surprising here, as the result relies on the well-known properties of ordinal numbers.
$(O,L,s)$
satisfying the three axioms above. There is nothing surprising here, as the result relies on the well-known properties of ordinal numbers. -
• Any triple
 $(O,L,s)$
satisfying these three axioms has an order which makes it order-isomorphic to the system of ordinal numbers. The order, in fact, is the specialization order of the topology given by the closure operator in the second axiom (without those axioms, this order is merely a preorder).
$(O,L,s)$
satisfying these three axioms has an order which makes it order-isomorphic to the system of ordinal numbers. The order, in fact, is the specialization order of the topology given by the closure operator in the second axiom (without those axioms, this order is merely a preorder). -
• The triple
 $(O,L,s)$
satisfying the three axioms above is an initial object in the category of all triples
$(O,L,s)$
satisfying the three axioms above is an initial object in the category of all triples
 $(O',L',s')$
such that
$(O',L',s')$
such that
 $\overline {I'}=\overline {J'}$
implies
$\overline {I'}=\overline {J'}$
implies
 $L(I')=L(J')$
, whenever those are defined (with the domain of
$L(I')=L(J')$
, whenever those are defined (with the domain of
 $L'$
being the class of all
$L'$
being the class of all
 $s'$
-closed subsets of
$s'$
-closed subsets of
 $O'$
).
$O'$
).
The idea for defining an ordinal number system abstractly goes back to Zermelo (see ‘Seven notes on ordinal numbers and large cardinals’ in [Reference Zermelo18]). His approach is to define it as a particular type of well-ordered class
![]() $(O,\leqslant )$
. The following axioms, added to well-ordering, would suffice:
$(O,\leqslant )$
. The following axioms, added to well-ordering, would suffice:
-
• For every
 $x\in O$
, the class
$x\in O$
, the class
 $\{x\}^> =\{y\in O\mid y<x\}$
is a set.
$\{x\}^> =\{y\in O\mid y<x\}$
is a set. -
• For each subset X of O, the class
 $X^< =\{y\in O\mid \forall _{x\in X}[x<y]\}$
is nonempty.
$X^< =\{y\in O\mid \forall _{x\in X}[x<y]\}$
is nonempty.
There is, of course, an analogous presentation (although less known than the one given by Peano axioms) of the natural number system as a well-ordered set
![]() $(N,\leqslant )$
satisfying the following additional conditions:
$(N,\leqslant )$
satisfying the following additional conditions:
-
• For each
 $x\in N$
, the set
$x\in N$
, the set
 $\{x\}^> $
is finite.
$\{x\}^> $
is finite. -
• For each
 $x\in N$
, the set
$x\in N$
, the set
 $\{x\}^< $
is nonempty.
$\{x\}^< $
is nonempty.
This is an alternative approach to that of Dedekind, where there is greater emphasis on the order structure. The difference between our approach to ordinal numbers and the traditional approaches is similar, where in our approach we try to make minimal use of the order structure. Universal properties of the ordinal number system emerging from the more order-based approach have been established, in various forms, in [Reference Joyal and Moerdijk8, Reference Rosický12]. Our universal property is different from those.
The main new results of the paper are given in the last section. Before that, we redevelop the basic theory of ordinal numbers relative to the set-theoretic context in which these results are proved, ensuring that the paper is self-contained.
This paper grew out from the second author’s rediscovery of Tarski’s addition of sets [Reference Tarski13] and of a universal property for ordinal numbers, known already from [Reference Rosický12]—see [Reference van der Berg14] (although, at the time of writing [Reference van der Berg14], the author was not aware of [Reference Rosický12]). Some of the chapters of [Reference van der Berg14] are based on the present paper (see also Remark 2).
2 The context
There are a number of alternatives for a context in which the theory that we lay down in this paper could be developed. Elaboration of those contexts and comparison of results across the contexts as a future development of our work would certainly be worthwhile. In this paper, we have decided to stick to what we believe to be technically the most simple and intuitive context, given by a ‘universe’ inside the standard Zermelo–Fraenkel axiomatic set theory, including the axioms of foundation and choice (see e.g. [Reference Jech7]). This approach is not unusual. For instance, it is the approach followed in the exposition of category theory in [Reference Lawvere11]. The universes we work with, however, are slightly more general than the more commonly used Grothendieck universes [Reference Bourbaki, Artin, Grothendieck and Verdier1, Reference Gabriel6, Reference Williams17]. The main difference is that our universes do not require closure under power sets and can be empty. Our context is in fact a particular instance of the quite general category-theoretic context used in [Reference Joyal and Moerdijk8]. Generalization of our results to that context is left for future work.
We remark that the definitions, theorems and their proofs contained in this paper could be adapted, after a straightforward modification to their formulation, to ‘absolute’ set theory, where our ‘sets’ could be replaced with ‘classes’ and elements of the fixed universe with ‘sets’. We would then get the form of the definitions and theorems given in Section 1.
For a set X, by
![]() $\mathsf {P} X$
we denote the power set of X, and by
$\mathsf {P} X$
we denote the power set of X, and by
![]() we denote the union of all elements of X. By
we denote the union of all elements of X. By
![]() $\mathbb {N}$
we denote the set of natural numbers. While we do not rely on any prior knowledge of facts about ordinal numbers (proofs of all needed facts are included in the paper), we do rely on knowledge of basic set-theoretic properties of the natural number system. In particular, we will make use of mathematical induction, definition by recursion, as well as the fact that any infinite set has a subset bijective to
$\mathbb {N}$
we denote the set of natural numbers. While we do not rely on any prior knowledge of facts about ordinal numbers (proofs of all needed facts are included in the paper), we do rely on knowledge of basic set-theoretic properties of the natural number system. In particular, we will make use of mathematical induction, definition by recursion, as well as the fact that any infinite set has a subset bijective to
![]() $\mathbb {N}$
.
$\mathbb {N}$
.
Recall that a set X is said to be transitive when
![]() $X\subseteq \mathsf {P} X$
, or equivalently, when
$X\subseteq \mathsf {P} X$
, or equivalently, when
![]() . For a function
. For a function
![]() $f\colon X\to Y$
and a set
$f\colon X\to Y$
and a set
![]() $A\in \mathsf {P} X$
, we write
$A\in \mathsf {P} X$
, we write
![]() $fA$
to denote the image of A under f:
$fA$
to denote the image of A under f:
Definition 1. A universe is a set
![]() $\mathfrak {U}$
satisfying the following:
$\mathfrak {U}$
satisfying the following:
-
(U1)
 $\mathfrak {U}$
is a transitive set.
$\mathfrak {U}$
is a transitive set. -
(U2) If
 $X,Y\in \mathfrak {U}$
then
$X,Y\in \mathfrak {U}$
then
 $\{X,Y\}\in \mathfrak {U}$
.
$\{X,Y\}\in \mathfrak {U}$
. -
(U3)
 for any
for any
 $I \in \mathfrak {U}$
and any function
$I \in \mathfrak {U}$
and any function
 $f\colon I\to \mathfrak {U}$
.
$f\colon I\to \mathfrak {U}$
.
These axioms imply that
![]() $\mathfrak {U}$
is closed under the following standard set-theoretic constructions:
$\mathfrak {U}$
is closed under the following standard set-theoretic constructions:
-
• Singletons. Trivially, since
 $\{x\}=\{x,x\}$
.
$\{x\}=\{x,x\}$
. -
• Union. Because
 .
. -
• Subsets. Let
 $Y\in \mathfrak {U}$
and let
$Y\in \mathfrak {U}$
and let
 $X\subseteq Y$
. If
$X\subseteq Y$
. If
 $X=\varnothing $
, then
$X=\varnothing $
, then
 $X\in \mathfrak {U}$
, because every nonempty transitive set contains the empty set thanks to the axiom of foundation. If
$X\in \mathfrak {U}$
, because every nonempty transitive set contains the empty set thanks to the axiom of foundation. If
 $X\neq \varnothing $
, then let
$X\neq \varnothing $
, then let
 $x_0\in X$
. Consider the function
$x_0\in X$
. Consider the function
 $f\colon Y\to \mathfrak {U}$
defined by Notice that
$f\colon Y\to \mathfrak {U}$
defined by Notice that $$ \begin{gather*} f(y)=\begin{cases} \{y\}, & y\in X,\\ \{x_0\}, & y\notin X. \end{cases} \end{gather*} $$
$$ \begin{gather*} f(y)=\begin{cases} \{y\}, & y\in X,\\ \{x_0\}, & y\notin X. \end{cases} \end{gather*} $$
 $\{x_0\}\in \mathfrak {U}$
since
$\{x_0\}\in \mathfrak {U}$
since
 $x_0 \in X \subseteq Y \in \mathfrak {U}$
and
$x_0 \in X \subseteq Y \in \mathfrak {U}$
and
 $\mathfrak {U}$
is a transitive set closed under singletons. Then
$\mathfrak {U}$
is a transitive set closed under singletons. Then
 .
.
-
• Cartesian products (binary). Let
 $X\in \mathfrak {U}$
and
$X\in \mathfrak {U}$
and
 $Y\in \mathfrak {U}$
. Then for each
$Y\in \mathfrak {U}$
. Then for each $$ \begin{gather*}\{(x,y)\}=\{\{\{x,y\},\{x\}\}\}\in\mathfrak{U}\end{gather*} $$
$$ \begin{gather*}\{(x,y)\}=\{\{\{x,y\},\{x\}\}\}\in\mathfrak{U}\end{gather*} $$
 $x\in X$
and
$x\in X$
and
 $y\in Y$
. For each
$y\in Y$
. For each
 $x\in X$
define a function
$x\in X$
define a function
 $f_x\colon Y\to \mathfrak {U}$
by
$f_x\colon Y\to \mathfrak {U}$
by
 $f_x(y)=\{(x,y)\}$
. Then
$f_x(y)=\{(x,y)\}$
. Then
 for each
for each
 $x\in X$
. Now define a function
$x\in X$
. Now define a function
 $g\colon X\to \mathfrak {U}$
by
$g\colon X\to \mathfrak {U}$
by
 $g(x)=\{\{(x,y)\mid y\in Y\}\}$
. Then
$g(x)=\{\{(x,y)\mid y\in Y\}\}$
. Then
 .
.
-
• Disjoint union. Given
 $X\in \mathfrak {U}$
, the disjoint union
$X\in \mathfrak {U}$
, the disjoint union
 can be defined as Then
can be defined as Then
 where
where
 $f\colon X\to \mathfrak {U}$
is defined by
$f\colon X\to \mathfrak {U}$
is defined by
 $f(x)=x\times \{x\}$
.
$f(x)=x\times \{x\}$
.
-
• Quotient sets. Let
 $X\in \mathfrak {U}$
and let E be an equivalence relation on X. Then
$X\in \mathfrak {U}$
and let E be an equivalence relation on X. Then
 , where q is the function
, where q is the function
 $q\colon X\to \mathfrak {U}$
defined by
$q\colon X\to \mathfrak {U}$
defined by
 $q(x)=\{[x]_E\}$
.
$q(x)=\{[x]_E\}$
. -
• Replacement. Let
 $X\in \mathfrak {U}$
and let f be a function
$X\in \mathfrak {U}$
and let f be a function
 $X\to \mathfrak {U}$
. By (a), we can define a function
$X\to \mathfrak {U}$
. By (a), we can define a function
 $g\colon \mathfrak {U} \to \mathfrak {U}$
such that
$g\colon \mathfrak {U} \to \mathfrak {U}$
such that
 $g(y) = \{y\}$
for each
$g(y) = \{y\}$
for each
 $y\in \mathfrak {U}$
. Then
$y\in \mathfrak {U}$
. Then
 $g\circ f$
is a function
$g\circ f$
is a function
 $X\to \mathfrak {U}$
such that for all
$X\to \mathfrak {U}$
such that for all
 $x\in X$
, The image of X under
$x\in X$
, The image of X under $$ \begin{align*} (g\circ f)(x) &= \{f(x) \}. \end{align*} $$
$$ \begin{align*} (g\circ f)(x) &= \{f(x) \}. \end{align*} $$
 $g\circ f$
is then Then by (U3),
$g\circ f$
is then Then by (U3), $$ \begin{align*} (g\circ f)X &= \{\{f(x)\}\mid x\in X \}. \end{align*} $$
$$ \begin{align*} (g\circ f)X &= \{\{f(x)\}\mid x\in X \}. \end{align*} $$

From this it follows, of course, that when
![]() $\mathfrak {U}$
is not empty, it contains all natural numbers, assuming that they are defined by the recursion
$\mathfrak {U}$
is not empty, it contains all natural numbers, assuming that they are defined by the recursion

Furthermore, when
![]() $\mathfrak {U}$
contains at least one infinite set, it also contains the set
$\mathfrak {U}$
contains at least one infinite set, it also contains the set
![]() $\mathbb {N}$
of all natural numbers (as defined above).
$\mathbb {N}$
of all natural numbers (as defined above).
The empty set
![]() $\varnothing $
is a universe. The sets whose transitive closure have cardinality less than a fixed infinite regular cardinal
$\varnothing $
is a universe. The sets whose transitive closure have cardinality less than a fixed infinite regular cardinal
![]() $\kappa $
form a universe in the sense of the definition above (by Lemma 6.4 in [Reference Kunen9]). In particular, hereditarily finite sets (where
$\kappa $
form a universe in the sense of the definition above (by Lemma 6.4 in [Reference Kunen9]). In particular, hereditarily finite sets (where
![]() $\kappa = \aleph _0$
) form a universe, as do hereditarily countable sets (where
$\kappa = \aleph _0$
) form a universe, as do hereditarily countable sets (where
![]() $\kappa = \aleph _1$
). The so-called Grothendieck universes are exactly those universes in our sense, which are closed under power sets, i.e., if
$\kappa = \aleph _1$
). The so-called Grothendieck universes are exactly those universes in our sense, which are closed under power sets, i.e., if
![]() $X\in \mathfrak {U}$
, then
$X\in \mathfrak {U}$
, then
![]() $\mathsf {P} X\in \mathfrak {U}$
.
$\mathsf {P} X\in \mathfrak {U}$
.
For any two sets A and B, we write
when there is a bijection from A to B. The restricted power set of a set X relative to a universe
![]() $\mathfrak {U}$
is the set
$\mathfrak {U}$
is the set
The following lemmas will be useful.
Lemma 2. When
![]() $\mathfrak {U}$
is nonempty, for any set X and its finite subset
$\mathfrak {U}$
is nonempty, for any set X and its finite subset
![]() $Y\subseteq X$
, we have
$Y\subseteq X$
, we have
![]() $Y\in \mathsf {P}_{\mathfrak {U}} X$
.
$Y\in \mathsf {P}_{\mathfrak {U}} X$
.
Proof. This follows from the fact that when
![]() $\mathfrak {U}$
is nonempty, it contains a set of each finite size.⊣
$\mathfrak {U}$
is nonempty, it contains a set of each finite size.⊣
Lemma 3. If
![]() $A\subseteq B$
and
$A\subseteq B$
and
![]() $B\in \mathsf {P}_{\mathfrak {U}} X$
, then
$B\in \mathsf {P}_{\mathfrak {U}} X$
, then
![]() $A\in \mathsf {P}_{\mathfrak {U}} X$
.
$A\in \mathsf {P}_{\mathfrak {U}} X$
.
Proof. If
![]() $A\subseteq B\approx C\in \mathfrak {U}$
, then A is bijective to a subset of C.⊣
$A\subseteq B\approx C\in \mathfrak {U}$
, then A is bijective to a subset of C.⊣
Lemma 4. If
![]() $C\in {\mathsf {P}}_{\mathfrak {U}}\mathsf {P}_{\mathfrak {U}} X$
then
$C\in {\mathsf {P}}_{\mathfrak {U}}\mathsf {P}_{\mathfrak {U}} X$
then
![]() . In particular, this implies that if
. In particular, this implies that if
![]() $I\in \mathsf {P}_{\mathfrak {U}} X$
, then for any function
$I\in \mathsf {P}_{\mathfrak {U}} X$
, then for any function
![]() $f\colon I\to \mathsf {P}_{\mathfrak {U}} X$
, we have
$f\colon I\to \mathsf {P}_{\mathfrak {U}} X$
, we have
![]() .
.
Proof. Suppose
![]() $C\in \mathsf {P}_{\mathfrak {U}} \mathsf {P}_{\mathfrak {U}} X$
. Then there is a bijection
$C\in \mathsf {P}_{\mathfrak {U}} \mathsf {P}_{\mathfrak {U}} X$
. Then there is a bijection
![]() $h\colon C'\to C$
, where
$h\colon C'\to C$
, where
![]() $C'\in \mathfrak {U}$
. Since for each element
$C'\in \mathfrak {U}$
. Since for each element
![]() $c\in C$
we have
$c\in C$
we have
![]() $c\in \mathsf {P}_{\mathfrak {U}} X$
, by axiom of choice we have a function
$c\in \mathsf {P}_{\mathfrak {U}} X$
, by axiom of choice we have a function
![]() $g\colon C\to \mathfrak {U}$
such that
$g\colon C\to \mathfrak {U}$
such that
![]() $c\approx g(c)$
for each
$c\approx g(c)$
for each
![]() $c\in C$
. Let
$c\in C$
. Let
![]() $g_c$
denote a bijection
$g_c$
denote a bijection
![]() $g_c\colon c\to g(c)$
(we again use the axiom of choice to select such a bijection for each
$g_c\colon c\to g(c)$
(we again use the axiom of choice to select such a bijection for each
![]() $c\in C$
). Now, define a function
$c\in C$
). Now, define a function
![]() $k\colon C'\to \mathfrak {U}$
as follows:
$k\colon C'\to \mathfrak {U}$
as follows:
Then
![]() by (U3). Consider the function
by (U3). Consider the function
![]() defined by
defined by
This function is a surjection. Indeed, for each
![]() there is a
there is a
![]() $c\in C$
such that
$c\in C$
such that
![]() $y\in c$
and so,
$y\in c$
and so,
 $$ \begin{align*} f(g_c(y),h^{-1}(c)) &=g^{-1}_{h(h^{-1}(c))}(g_c(y))\\ &=g^{-1}_c(g_c(y))\\ &=y. \end{align*} $$
$$ \begin{align*} f(g_c(y),h^{-1}(c)) &=g^{-1}_{h(h^{-1}(c))}(g_c(y))\\ &=g^{-1}_c(g_c(y))\\ &=y. \end{align*} $$
So
![]() is bijective to a quotient set of
is bijective to a quotient set of
![]() , and thus
, and thus
![]() . This proves the first part of the lemma.
. This proves the first part of the lemma.
Now suppose
![]() $I\in \mathsf {P}_{\mathfrak {U}} X$
and let
$I\in \mathsf {P}_{\mathfrak {U}} X$
and let
![]() $f\colon I\to \mathsf {P}_{\mathfrak {U}} X$
be a function. Then
$f\colon I\to \mathsf {P}_{\mathfrak {U}} X$
be a function. Then
![]() $fI\in \mathsf {P}_{\mathfrak {U}} \mathsf {P}_{\mathfrak {U}} X$
. By what we have just proved,
$fI\in \mathsf {P}_{\mathfrak {U}} \mathsf {P}_{\mathfrak {U}} X$
. By what we have just proved,
![]() .⊣
.⊣
Lemma 5. Given a function
![]() $f\colon X\to Y$
,
$f\colon X\to Y$
,
Proof. If
![]() $A\approx A'\in \mathfrak {U}$
, then
$A\approx A'\in \mathfrak {U}$
, then
![]() $fA$
is bijective to a suitable quotient of
$fA$
is bijective to a suitable quotient of
![]() $A'$
.⊣
$A'$
.⊣
Lemma 6. If
![]() $A\in \mathsf {P}_{\mathfrak {U}} X$
and
$A\in \mathsf {P}_{\mathfrak {U}} X$
and
![]() $B\in \mathsf {P}_{\mathfrak {U}} Y$
, then
$B\in \mathsf {P}_{\mathfrak {U}} Y$
, then
![]() $A\times B\in \mathsf {P}_{\mathfrak {U}} (X\times Y)$
.
$A\times B\in \mathsf {P}_{\mathfrak {U}} (X\times Y)$
.
Proof. This follows from the fact that
![]() $\mathfrak {U}$
is closed under cartesian products.⊣
$\mathfrak {U}$
is closed under cartesian products.⊣
Lemma 7.
![]() $\mathsf {P}_{\mathfrak {U}} \mathfrak {U} = \mathfrak {U}$
.
$\mathsf {P}_{\mathfrak {U}} \mathfrak {U} = \mathfrak {U}$
.
Proof. Let
![]() $A\in \mathsf {P}_{\mathfrak {U}} \mathfrak {U}$
, i.e.,
$A\in \mathsf {P}_{\mathfrak {U}} \mathfrak {U}$
, i.e.,
![]() $A\subseteq \mathfrak {U}$
such that
$A\subseteq \mathfrak {U}$
such that
![]() $A\approx B\in \mathfrak {U}$
. Then a bijection
$A\approx B\in \mathfrak {U}$
. Then a bijection
![]() $f\colon B\to A$
exists, and since
$f\colon B\to A$
exists, and since
![]() $A\subseteq \mathfrak {U}$
, this gives us
$A\subseteq \mathfrak {U}$
, this gives us
![]() $A = fB \in \mathfrak {U}$
.
$A = fB \in \mathfrak {U}$
.
Now consider
![]() $A\in \mathfrak {U}$
. Then
$A\in \mathfrak {U}$
. Then
![]() $A\subseteq \mathfrak {U}$
by (U1), and since
$A\subseteq \mathfrak {U}$
by (U1), and since
![]() $A\approx A\in \mathfrak {U}$
, this gives us
$A\approx A\in \mathfrak {U}$
, this gives us
![]() $A\in \mathsf {P}_{\mathfrak {U}} \mathfrak {U}$
. We can conclude that
$A\in \mathsf {P}_{\mathfrak {U}} \mathfrak {U}$
. We can conclude that
![]() $\mathsf {P}_{\mathfrak {U}} \mathfrak {U} = \mathfrak {U}$
.⊣
$\mathsf {P}_{\mathfrak {U}} \mathfrak {U} = \mathfrak {U}$
.⊣
Remark. One could relax the context proposed in this section by dropping the axiom of foundation and adopting an axiom on
![]() $\mathfrak {U}$
stating that if it
$\mathfrak {U}$
stating that if it
![]() $\mathfrak {U}$
is non-empty, then it must contain the empty set—see [Reference van der Berg14]. We have refrained from adopting this weaker context in the present paper, as it would result in a slightly more technical presentation of the background material (especially the material on concrete ordinals), without a significant gain in generality.
$\mathfrak {U}$
is non-empty, then it must contain the empty set—see [Reference van der Berg14]. We have refrained from adopting this weaker context in the present paper, as it would result in a slightly more technical presentation of the background material (especially the material on concrete ordinals), without a significant gain in generality.
3 Abstract ordinals
In this section we introduce an abstract notion of an ordinal number system relative to a universe and establish its basic properties. Consider a partially ordered set
![]() $(X,\leqslant )$
. The relation
$(X,\leqslant )$
. The relation
![]() $<$
for the partial order, as a relation from X to X, induces a Galois connection from
$<$
for the partial order, as a relation from X to X, induces a Galois connection from
![]() $\mathsf {P} X$
to itself given by the mappings
$\mathsf {P} X$
to itself given by the mappings
 $$ \begin{align*} S\mapsto S^> &= \{x\in X\mid \forall_{y\in S} [x<y]\}\text{ and}\\ S\mapsto S^< &= \{x\in X\mid \forall_{y\in S} [y<x]\}. \end{align*} $$
$$ \begin{align*} S\mapsto S^> &= \{x\in X\mid \forall_{y\in S} [x<y]\}\text{ and}\\ S\mapsto S^< &= \{x\in X\mid \forall_{y\in S} [y<x]\}. \end{align*} $$
We call
![]() $S^> $
the lower complement of S, and
$S^> $
the lower complement of S, and
![]() $S^< $
the upper complement of S. Note that by ‘
$S^< $
the upper complement of S. Note that by ‘
![]() $a<b$
’ above we mean ‘
$a<b$
’ above we mean ‘
![]() $a\leqslant b\land a\neq b$
’, as usual. Since the two mappings above form a Galois connection, we have
$a\leqslant b\land a\neq b$
’, as usual. Since the two mappings above form a Galois connection, we have
for any
![]() $S\subseteq X$
. We define the incremented join
$S\subseteq X$
. We define the incremented join
of a subset S of X (when it exists) as follows:
Note that since
![]() $S\cap S^< =\varnothing $
, the incremented join of S is never an element of S.
$S\cap S^< =\varnothing $
, the incremented join of S is never an element of S.
It will be convenient to use the following abbreviations (where
![]() $x\in X$
and
$x\in X$
and
![]() $S\subseteq X$
):
$S\subseteq X$
):
The following basic laws are self-evident:
-
(L1)
 $x<x^+ $
,
$x<x^+ $
, -
(L2) there is no z such that
 $x<z<x^+ $
,
$x<z<x^+ $
, -
(L3)
 $x<y \;\Leftrightarrow \; x^+ \leqslant y$
,
$x<y \;\Leftrightarrow \; x^+ \leqslant y$
, -
(L4)
 (for a total order),
(for a total order), -
(L5)
 $x<y^+ \;\Leftrightarrow \;x\leqslant y $
(for a total order),
$x<y^+ \;\Leftrightarrow \;x\leqslant y $
(for a total order), -
(L6)
 $x^+ =y^+ \;\Leftrightarrow \; x=y$
(for a total order),
$x^+ =y^+ \;\Leftrightarrow \; x=y$
(for a total order), -
(L7)
 $x<y \;\Leftrightarrow \; x^+ <y^+ $
(for a total order).
$x<y \;\Leftrightarrow \; x^+ <y^+ $
(for a total order).
Using (L3), we can establish the following:
Lemma 8. For any
![]() $S\subseteq X$
, if
$S\subseteq X$
, if
![]() $x^+$
exists for all
$x^+$
exists for all
![]() $x\in S$
, then
$x\in S$
, then
exists if and only if
exists, and when they exist,
The following (easy) lemma will also be useful:
Lemma 9. Let
![]() $(X,\leqslant )$
be a poset and let
$(X,\leqslant )$
be a poset and let
![]() $S\subseteq X$
. Then:
$S\subseteq X$
. Then:
-
(i) If S does not have a largest element, then
 exists if and only if
exists if and only if
 exists, and when they exist,
exists, and when they exist,
 . Conversely, if
. Conversely, if
 , then S does not have a largest element.
, then S does not have a largest element. -
(ii) If S has a largest element
 $x=\mathop {\mathsf {max}} S$
, then
$x=\mathop {\mathsf {max}} S$
, then
 exists if and only if
exists if and only if
 $x^+ $
exists, and when they exist,
$x^+ $
exists, and when they exist,
 . Conversely, when
. Conversely, when
 $\leqslant $
is a total order, if
$\leqslant $
is a total order, if
 then
then
 $x=\mathop {\mathsf {max}} S$
.
$x=\mathop {\mathsf {max}} S$
. -
(iii) If
 exists then
exists then
 . Conversely, when
. Conversely, when
 $\leqslant $
is a total order, if
$\leqslant $
is a total order, if
 $\mathop {\mathsf {min}} S$
exists, then
$\mathop {\mathsf {min}} S$
exists, then
 .
.
Proof.
-
(i) If S has no largest element, then
and so $$ \begin{gather*} \{x\in X\mid \forall _{y\in S}[y\leqslant x] \}=\{x\in X\mid \forall _{y\in S}[y<x] \} \end{gather*} $$
exists if and only if
$$ \begin{gather*} \{x\in X\mid \forall _{y\in S}[y\leqslant x] \}=\{x\in X\mid \forall _{y\in S}[y<x] \} \end{gather*} $$
exists if and only if exists, and when they exist, they are equal. Now suppose
exists, and when they exist, they are equal. Now suppose
 . Since
. Since
 is never an element of S, we conclude that S does not have a largest element.
is never an element of S, we conclude that S does not have a largest element.
-
(ii) Let
 $x=\mathop {\mathsf {max}} S$
. Then
$x=\mathop {\mathsf {max}} S$
. Then
 $\{x\}^< =S^< $
, and so
$\{x\}^< =S^< $
, and so
 $x^+=\mathop {\mathsf {min}} \{x\}^<$
exists if and only if
$x^+=\mathop {\mathsf {min}} \{x\}^<$
exists if and only if
 exists, and when they exist, they are equal. Now suppose, in the case of total order, that
exists, and when they exist, they are equal. Now suppose, in the case of total order, that
 for some
for some
 $x\in X$
. Then S can only have elements that are strictly smaller than
$x\in X$
. Then S can only have elements that are strictly smaller than
 $x^+ $
, and thus each element of S is less than or equal to x (L5). Also, since
$x^+ $
, and thus each element of S is less than or equal to x (L5). Also, since
 , it does not hold that
, it does not hold that
 $x\in S^< $
, and thus x is not strictly larger than every element of S. We can conclude that
$x\in S^< $
, and thus x is not strictly larger than every element of S. We can conclude that
 $x=\mathop {\mathsf {max}} S$
.
$x=\mathop {\mathsf {max}} S$
. -
(iii) Suppose
 exists. Since
exists. Since
 $S\subseteq (S^> )^< $
, we must have
$S\subseteq (S^> )^< $
, we must have
 for each
for each
 $x\in S$
. This together with the fact that
$x\in S$
. This together with the fact that
 cannot be an element of
cannot be an element of
 $S^> $
forces
$S^> $
forces
 to be an element of S. Hence
to be an element of S. Hence
 . Suppose now that
. Suppose now that
 $\leqslant $
is a total order and
$\leqslant $
is a total order and
 $\mathop {\mathsf {min}} S$
exists. Consider an element
$\mathop {\mathsf {min}} S$
exists. Consider an element
 $x\in (S^> )^< $
. Then x is not an element of
$x\in (S^> )^< $
. Then x is not an element of
 $S^> $
and so we cannot have
$S^> $
and so we cannot have
 $x<\mathop {\mathsf {min}} S$
. Therefore,
$x<\mathop {\mathsf {min}} S$
. Therefore,
 $\mathop {\mathsf {min}} S\leqslant x$
. This proves
$\mathop {\mathsf {min}} S\leqslant x$
. This proves
 .⊣
.⊣
Definition 10. An ordinal system relative to a universe
![]() $\mathfrak {U}$
is a partially ordered set
$\mathfrak {U}$
is a partially ordered set
![]() $\mathcal {O}=(\mathcal {O},\leqslant )$
satisfying the following axioms:
$\mathcal {O}=(\mathcal {O},\leqslant )$
satisfying the following axioms:
-
(O1) For all
 $X\subseteq \mathcal {O}$
, if
$X\subseteq \mathcal {O}$
, if
 $X\neq \varnothing $
, then
$X\neq \varnothing $
, then
 $X^> \in \mathsf {P}_{\mathfrak {U}} \mathcal {O}$
.
$X^> \in \mathsf {P}_{\mathfrak {U}} \mathcal {O}$
. -
(O2)
 exists for each
exists for each
 $X\in \mathsf {P}_{\mathfrak {U}} \mathcal {O}$
.
$X\in \mathsf {P}_{\mathfrak {U}} \mathcal {O}$
.
We refer to elements of
![]() $\mathcal {O}$
as ordinals.
$\mathcal {O}$
as ordinals.
Note that if
![]() $\mathcal {O}$
is nonempty, then Axiom (O1) forces the universe
$\mathcal {O}$
is nonempty, then Axiom (O1) forces the universe
![]() $\mathfrak {U}$
to be nonempty as well. So for any ordinal
$\mathfrak {U}$
to be nonempty as well. So for any ordinal
![]() $x\in \mathcal {O}$
, we have
$x\in \mathcal {O}$
, we have
![]() $\{x\}\in \mathsf {P}_{\mathfrak {U}} \mathcal {O}$
(Lemma 2). Note also that Axiom (O1) is equivalent to its weaker form (the equivalence does not require (O2) and relies on Lemma 3):
$\{x\}\in \mathsf {P}_{\mathfrak {U}} \mathcal {O}$
(Lemma 2). Note also that Axiom (O1) is equivalent to its weaker form (the equivalence does not require (O2) and relies on Lemma 3):
-
(O1′)
 $\{x\}^> \in \mathsf {P}_{\mathfrak {U}} \mathcal {O}$
for all
$\{x\}^> \in \mathsf {P}_{\mathfrak {U}} \mathcal {O}$
for all
 $x\in \mathcal {O}$
.
$x\in \mathcal {O}$
.
Axiom (O2) implies that the mapping
![]() $x\mapsto x^+$
is a function
$x\mapsto x^+$
is a function
![]() $ \mathcal {O}\to \mathcal {O}$
. We call this function the successor function of the ordinal system
$ \mathcal {O}\to \mathcal {O}$
. We call this function the successor function of the ordinal system
![]() $\mathcal {O}$
. For each
$\mathcal {O}$
. For each
![]() $x\in \mathcal {O}$
, an element of
$x\in \mathcal {O}$
, an element of
![]() $\mathcal {O}$
that has the form
$\mathcal {O}$
that has the form
![]() $x^+$
is called a successor ordinal and the successor of x. We call an ordinal that is not a successor ordinal a limit ordinal.
$x^+$
is called a successor ordinal and the successor of x. We call an ordinal that is not a successor ordinal a limit ordinal.
Recall that a poset is a well-ordered set when each of its nonempty subsets has a smallest element.
Theorem 11. A poset
![]() $(\mathcal {O},\leqslant )$
is an ordinal system relative to a universe
$(\mathcal {O},\leqslant )$
is an ordinal system relative to a universe
![]() $\mathfrak {U}$
if and only if it is a well-ordered set (and consecutively, a totally ordered set) satisfying (O1
$\mathfrak {U}$
if and only if it is a well-ordered set (and consecutively, a totally ordered set) satisfying (O1
![]() ${}^{\prime }$
) and such that
${}^{\prime }$
) and such that
![]() $X^< \neq \varnothing $
for all
$X^< \neq \varnothing $
for all
![]() $X\in {\mathsf {P}}_{\mathfrak {U}} (\mathcal {O})$
.
$X\in {\mathsf {P}}_{\mathfrak {U}} (\mathcal {O})$
.
Proof. Consider an ordinal system
![]() $\mathcal {O}$
relative to a universe
$\mathcal {O}$
relative to a universe
![]() $\mathfrak {U}$
. Let X be a nonempty subset of
$\mathfrak {U}$
. Let X be a nonempty subset of
![]() $\mathcal {O}$
. Then
$\mathcal {O}$
. Then
![]() $X^> \in {\mathsf {P}}_{\mathfrak {U}} \mathcal {O}$
by (O1), and thus
$X^> \in {\mathsf {P}}_{\mathfrak {U}} \mathcal {O}$
by (O1), and thus
![]() exists by (O2). By Lemma 9(iii),
exists by (O2). By Lemma 9(iii),
![]() . This proves the ‘only if’ part of the theorem. Note that any well-ordered set is totally ordered: having a smallest element of a two-element subset
. This proves the ‘only if’ part of the theorem. Note that any well-ordered set is totally ordered: having a smallest element of a two-element subset
![]() $\{x,y \}$
forces x and y to be comparable. The ‘if’ part is quite obvious.⊣
$\{x,y \}$
forces x and y to be comparable. The ‘if’ part is quite obvious.⊣
We will use this theorem often without referring to it. One of its consequences is that each nonempty ordinal system has a smallest element. We denote this element by
![]() $0$
. Note that
$0$
. Note that
![]() $0$
is a limit ordinal. Since by the same theorem an ordinal system is a total order, the properties (L4–7) above apply to an ordinal system. In particular, we get that the successor function is injective. We also get the following:
$0$
is a limit ordinal. Since by the same theorem an ordinal system is a total order, the properties (L4–7) above apply to an ordinal system. In particular, we get that the successor function is injective. We also get the following:
Lemma 12. In an ordinal system, for an ordinal x the following conditions are equivalent:
-
(i) x is a limit ordinal.
-
(ii)
 $\{x\}^>$
is closed under successors.
$\{x\}^>$
is closed under successors. -
(iii)
 .
.
Proof. We have
![]() for any ordinal x (L4). If x is a limit ordinal then for each
for any ordinal x (L4). If x is a limit ordinal then for each
![]() $y<x$
we have
$y<x$
we have
![]() $y^+<x$
(L3). So (i)
$y^+<x$
(L3). So (i)
![]() ${}\Rightarrow {}$
(ii). If (ii) holds, by (L1), we get that
${}\Rightarrow {}$
(ii). If (ii) holds, by (L1), we get that
![]() $\{x\}^>$
does not have a largest element. So
$\{x\}^>$
does not have a largest element. So
![]() (Lemma 9). This gives (ii)
(Lemma 9). This gives (ii)
![]() ${}\Rightarrow {}$
(iii). Suppose now
${}\Rightarrow {}$
(iii). Suppose now
![]() . If x were a successor ordinal
. If x were a successor ordinal
![]() $x=y^+$
, then by (L5), y would be the join of
$x=y^+$
, then by (L5), y would be the join of
![]() $\{x\}^>$
. However,
$\{x\}^>$
. However,
![]() $x\neq y$
by (L1), and therefore, x must be a limit ordinal. Thus, (iii)
$x\neq y$
by (L1), and therefore, x must be a limit ordinal. Thus, (iii)
![]() ${}\Rightarrow {}$
(i).⊣
${}\Rightarrow {}$
(i).⊣
The following theorem gives yet another way of thinking about an ordinal system.
Theorem 13. A poset
![]() $(\mathcal {O},\leqslant )$
is an ordinal system relative to a universe
$(\mathcal {O},\leqslant )$
is an ordinal system relative to a universe
![]() $\mathfrak {U}$
if and only if (O1) holds along with the following axioms:
$\mathfrak {U}$
if and only if (O1) holds along with the following axioms:
-
(O2a) For all
 $X\in {\mathsf {P}}_{\mathfrak {U}} \mathcal {O}$
, the join
$X\in {\mathsf {P}}_{\mathfrak {U}} \mathcal {O}$
, the join
 exists.
exists. -
(O2b)
 $x^+$
exists for each
$x^+$
exists for each
 $x\in {\mathcal {O}}$
.
$x\in {\mathcal {O}}$
.
Proof. This can easily be proved using (i) and (ii) of Lemma 9.⊣
Transfinite induction and recursion are well known for well-ordered sets. We formulate them here (in one particular form, out of many possibilities) in the case of ordinal systems, since we will use them later on in the paper. We have included our own direct proofs, for the sake of completeness, but we do not expect these proofs to have any new arguments that do not already exist in the literature.
Theorem 14 (transfinite induction)
Let
![]() $\mathcal {O}$
be an ordinal system and let
$\mathcal {O}$
be an ordinal system and let
![]() $X\subseteq \mathcal {O}$
satisfy the following conditions:
$X\subseteq \mathcal {O}$
satisfy the following conditions:
-
(I1)
 $X^+ \subseteq X;$
$X^+ \subseteq X;$
-
(I2) for every limit ordinal x, if
 $\{x\}^> \subseteq X$
then
$\{x\}^> \subseteq X$
then
 $x\in X$
.
$x\in X$
.
Then
![]() $X=\mathcal {O}$
.
$X=\mathcal {O}$
.
Proof. Since
![]() $\mathcal {O}$
is well-ordered, if
$\mathcal {O}$
is well-ordered, if
![]() $\mathcal {O} \setminus X$
is nonempty, then it has a smallest element y. By (I1), y cannot be a successor of any
$\mathcal {O} \setminus X$
is nonempty, then it has a smallest element y. By (I1), y cannot be a successor of any
![]() $z<y$
in X. By (I2), it also cannot be a limit ordinal. This is a contradiction, since a limit ordinal is defined as one that is not a successor ordinal.⊣
$z<y$
in X. By (I2), it also cannot be a limit ordinal. This is a contradiction, since a limit ordinal is defined as one that is not a successor ordinal.⊣
Here is one of the immediate consequences of transfinite induction (the proof will require also the total order of an ordinal system, as well as the properties (L3) and (L4)):
Corollary 15. Let
![]() $\mathcal {O}$
be an ordinal system relative to a universe
$\mathcal {O}$
be an ordinal system relative to a universe
![]() $\mathfrak {U}$
, and let
$\mathfrak {U}$
, and let
![]() $X\subseteq \mathcal {O}$
satisfy the following conditions:
$X\subseteq \mathcal {O}$
satisfy the following conditions:
-
(S1) X is down-closed in
 $\mathcal {O}$
, i.e., if
$\mathcal {O}$
, i.e., if
 $x<y\in X$
then
$x<y\in X$
then
 $x\in X$
, for all
$x\in X$
, for all
 $x,y\in \mathcal {O}$
;
$x,y\in \mathcal {O}$
; -
(S2) X is an ordinal system relative to
 $\mathfrak {U}$
under the restriction of the order of
$\mathfrak {U}$
under the restriction of the order of
 $\mathcal {O}$
.
$\mathcal {O}$
.
Then
![]() $X=\mathcal {O}$
.
$X=\mathcal {O}$
.
Theorem 16 (transfinite recursion)
Let
![]() $\mathcal {O}$
be an ordinal system and let
$\mathcal {O}$
be an ordinal system and let
![]() $X=(X,L,s)$
, where X is a set, s is a function
$X=(X,L,s)$
, where X is a set, s is a function
![]() $X\to X$
, and L is a function
$X\to X$
, and L is a function
![]() $\mathsf {P}_{\mathfrak {U}} X\to X$
. Then there exists a unique function
$\mathsf {P}_{\mathfrak {U}} X\to X$
. Then there exists a unique function
![]() $f\colon \mathcal {O}\to X$
that satisfies the following conditions:
$f\colon \mathcal {O}\to X$
that satisfies the following conditions:
-
(R1)
 $f(x^+ ) = s(f(x))$
for any
$f(x^+ ) = s(f(x))$
for any
 $x\in \mathcal {O}$
;
$x\in \mathcal {O}$
; -
(R2)
 $f(x) = L(\{f(y)\mid y<x \})$
for any limit ordinal x.
$f(x) = L(\{f(y)\mid y<x \})$
for any limit ordinal x.
Proof. For each ordinal
![]() $x\in \mathcal {O}$
, let
$x\in \mathcal {O}$
, let
![]() $F_x$
be the set consisting of all functions
$F_x$
be the set consisting of all functions
that satisfy the following conditions:
-
(i)
 $f(y^+ ) = s(f(y))$
for any successor ordinal
$f(y^+ ) = s(f(y))$
for any successor ordinal
 $y^+ \leqslant x$
, and
$y^+ \leqslant x$
, and -
(ii)
 $f(y) = L(\{f(z)\mid z<y \})$
for any limit ordinal
$f(y) = L(\{f(z)\mid z<y \})$
for any limit ordinal
 $y\leqslant x$
.
$y\leqslant x$
.
Note that any function f satisfying (R1–2) must have a subfunction in each set
![]() $F_x$
. Also, for any
$F_x$
. Also, for any
![]() $x\in \mathcal {O}$
, a function
$x\in \mathcal {O}$
, a function
![]() $f_x\in F_x$
must have a subfunction in each set
$f_x\in F_x$
must have a subfunction in each set
![]() $F_y$
where
$F_y$
where
![]() $y<x$
. We prove by transfinite induction that for each
$y<x$
. We prove by transfinite induction that for each
![]() $x\in \mathcal {O}$
, the set
$x\in \mathcal {O}$
, the set
![]() $F_x$
contains exactly one function
$F_x$
contains exactly one function
![]() $f_x$
.
$f_x$
.
Successor case: Suppose that for some ordinal x and each
![]() $y\leqslant x$
there exists a unique function
$y\leqslant x$
there exists a unique function
![]() $f_y\in F_y$
. Then
$f_y\in F_y$
. Then
![]() satisfies (i) and (ii), and thus
satisfies (i) and (ii), and thus
![]() $g\in F_{x^+ }$
.
$g\in F_{x^+ }$
.
Now consider any function
![]() $g'\in F_{x^+ }$
. Since g and
$g'\in F_{x^+ }$
. Since g and
![]() $g'$
must each have the unique function
$g'$
must each have the unique function
![]() $f_x\in F_x$
as a subfunction, g and
$f_x\in F_x$
as a subfunction, g and
![]() $g'$
are identical on the domain
$g'$
are identical on the domain
![]() $\{y\mid y\leqslant x \}$
. However, since g and
$\{y\mid y\leqslant x \}$
. However, since g and
![]() $g'$
each satisfies condition (i), we get that
$g'$
each satisfies condition (i), we get that
![]() $g'(x^+ ) = s(f_x(x)) = g(x^+ )$
, and thus
$g'(x^+ ) = s(f_x(x)) = g(x^+ )$
, and thus
![]() $g'=g$
is the unique function in
$g'=g$
is the unique function in
![]() $F_{x^+}$
.
$F_{x^+}$
.
Limit case: Suppose that for some limit ordinal x and each
![]() $y<x$
there exists a unique function
$y<x$
there exists a unique function
![]() $f_y\in F_y$
. Then, for any two ordinals
$f_y\in F_y$
. Then, for any two ordinals
![]() $y<y'<x$
, the function
$y<y'<x$
, the function
![]() $f_y$
is a subfunction of
$f_y$
is a subfunction of
![]() $f_{y'}$
, which is in turn a subfunction of every function in
$f_{y'}$
, which is in turn a subfunction of every function in
![]() $F_x$
. The relation
$F_x$
. The relation
is then a function over the domain
![]() $\{y\mid y\leqslant x\}$
and, moreover, it is easy to see that
$\{y\mid y\leqslant x\}$
and, moreover, it is easy to see that
![]() $g\in F_x$
.
$g\in F_x$
.
Now consider any function
![]() $g'\in F_x$
. Since for each ordinal
$g'\in F_x$
. Since for each ordinal
![]() $y<x$
the unique function
$y<x$
the unique function
![]() $f_y\in F_y$
is a subfunction of both g and
$f_y\in F_y$
is a subfunction of both g and
![]() $g'$
, we see that they are identical on the domain
$g'$
, we see that they are identical on the domain
![]() $\{y\mid y<x \}$
, and since they both satisfy condition (ii), the following holds:
$\{y\mid y<x \}$
, and since they both satisfy condition (ii), the following holds:
We can conclude that
![]() $g'=g$
is the unique function in
$g'=g$
is the unique function in
![]() $F_{x}$
.
$F_{x}$
.
We showed that for each ordinal x, exactly one function
![]() $f_x\in F_x$
exists. Construct a function
$f_x\in F_x$
exists. Construct a function
![]() $f\colon \mathcal {O}\to X$
as follows: for each ordinal x,
$f\colon \mathcal {O}\to X$
as follows: for each ordinal x,
It satisfies (R1–2) because each
![]() $f_x$
satisfies (i) and (ii). Since any function satisfying (R1–2) must have a subfunction in each set
$f_x$
satisfies (i) and (ii). Since any function satisfying (R1–2) must have a subfunction in each set
![]() $F_x$
, we can conclude that f is the unique function satisfying (R1–2).⊣
$F_x$
, we can conclude that f is the unique function satisfying (R1–2).⊣
4 Concrete ordinals
For a universe
![]() $\mathfrak {U}$
, define a
$\mathfrak {U}$
, define a
![]() $\mathfrak {U}$
-ordinal to be a transitive set that belongs to the universe
$\mathfrak {U}$
-ordinal to be a transitive set that belongs to the universe
![]() $\mathfrak {U}$
and is a well-ordered set under the relation
$\mathfrak {U}$
and is a well-ordered set under the relation
Thus, a
![]() $\mathfrak {U}$
-ordinal is nothing but a usual von Neumann ordinal number [Reference von Neumann15] that happens to be an element of
$\mathfrak {U}$
-ordinal is nothing but a usual von Neumann ordinal number [Reference von Neumann15] that happens to be an element of
![]() $\mathfrak {U}$
. In other words, it is a von Neumann ordinal number internal to the universe
$\mathfrak {U}$
. In other words, it is a von Neumann ordinal number internal to the universe
![]() $\mathfrak {U}$
. Thus, at least one direction in the following theorem is well known. We include a full proof for completeness.
$\mathfrak {U}$
. Thus, at least one direction in the following theorem is well known. We include a full proof for completeness.
Theorem 17. A set O is the set of all
![]() $\mathfrak {U}$
-ordinals if and only if the following conditions hold:
$\mathfrak {U}$
-ordinals if and only if the following conditions hold:
-
(a)
 $O \subseteq \mathfrak {U}$
, and if
$O \subseteq \mathfrak {U}$
, and if
 $\varnothing \in \mathfrak {U}$
, then
$\varnothing \in \mathfrak {U}$
, then
 $\varnothing \in O$
;
$\varnothing \in O$
; -
(b) O is a transitive set;
-
(c) O is an ordinal system relative to
 $\mathfrak {U}$
under the relation
$\mathfrak {U}$
under the relation
 , with the corresponding strict ordering given by
, with the corresponding strict ordering given by
 $\in $
.
$\in $
.
When these conditions hold, the incremented join of
![]() $X\in \mathsf {P}_{\mathfrak {U}} O$
is given by
$X\in \mathsf {P}_{\mathfrak {U}} O$
is given by
![]() .
.
Proof. We prove both directions. The proof of the last statement in the theorem is included in Step 1(c).
Step 1. We prove that if O is the set of all
![]() $\mathfrak {U}$
-ordinals, then (a–c) hold. While proving (c), we show that the incremented join of a set of
$\mathfrak {U}$
-ordinals, then (a–c) hold. While proving (c), we show that the incremented join of a set of
![]() $\mathfrak {U}$
-ordinals
$\mathfrak {U}$
-ordinals
![]() $X\in \mathsf {P}_{\mathfrak {U}} O$
is given by
$X\in \mathsf {P}_{\mathfrak {U}} O$
is given by
![]() .
.
Let O be the set of all
![]() $\mathfrak {U}$
-ordinals.
$\mathfrak {U}$
-ordinals.
-
(a) This follows easily from the definition of a
 $\mathfrak {U}$
-ordinal as a transitive element of
$\mathfrak {U}$
-ordinal as a transitive element of
 $\mathfrak {U}$
.
$\mathfrak {U}$
. -
(b) To prove transitivity, let
 $y\in x\in O$
. We want to show that y is a
$y\in x\in O$
. We want to show that y is a
 $\mathfrak {U}$
-ordinal (i.e., an element of
$\mathfrak {U}$
-ordinal (i.e., an element of
 $\mathfrak {U}$
that is transitive and well-ordered by
$\mathfrak {U}$
that is transitive and well-ordered by
 ). Since
). Since
 $x\in \mathfrak {U}$
, we have
$x\in \mathfrak {U}$
, we have
 $y\in \mathfrak {U}$
by (U1). Since y is a subset of the well-ordered set x, y must also be well-ordered.
$y\in \mathfrak {U}$
by (U1). Since y is a subset of the well-ordered set x, y must also be well-ordered.Next, we must prove that y is transitive. Let
 $z\in y$
. Then
$z\in y$
. Then
 $z\in x$
, since x is transitive. We want to show that
$z\in x$
, since x is transitive. We want to show that
 $z\subseteq y$
, so suppose
$z\subseteq y$
, so suppose
 $t\in z$
. Then
$t\in z$
. Then
 $t\in x$
, by transitivity of x. By the fact that
$t\in x$
, by transitivity of x. By the fact that
 is a total order on x, we must have
is a total order on x, we must have
 . We cannot have
. We cannot have
 $t=y$
, since
$t=y$
, since
 $t\in z\in y$
, and so
$t\in z\in y$
, and so
 $t\in y$
.
$t\in y$
. -
(c) We use the characterization of an ordinal system given in Theorem 11(b) as a well-ordered set satisfying (O1
 ${}^{\prime }$
), in which
${}^{\prime }$
), in which
 $X^<\neq \varnothing $
holds for all
$X^<\neq \varnothing $
holds for all
 $X\in \mathsf {P}_{\mathfrak {U}} O$
.
$X\in \mathsf {P}_{\mathfrak {U}} O$
.Notice that the relation
 is a partial order on O: reflexivity is obvious, while transitivity follows from each element of O being a transitive set. By the axiom of foundation,
is a partial order on O: reflexivity is obvious, while transitivity follows from each element of O being a transitive set. By the axiom of foundation,
 $\in $
is the strict ordering on O corresponding to
$\in $
is the strict ordering on O corresponding to
 .
.We can easily prove, as follows, that O satisfies (O1
 ${}^{\prime }$
).
${}^{\prime }$
).-
O1 ′. Consider
 $x\in O$
. Then we have: Since x is a
$x\in O$
. Then we have: Since x is a $$ \begin{gather*} \{x\}^> = \{y\in O\mid y\in x\}\subseteq x. \end{gather*} $$
$$ \begin{gather*} \{x\}^> = \{y\in O\mid y\in x\}\subseteq x. \end{gather*} $$
 $\mathfrak {U}$
-ordinal,
$\mathfrak {U}$
-ordinal,
 $x\in \mathsf {P}_{\mathfrak {U}} O$
and so
$x\in \mathsf {P}_{\mathfrak {U}} O$
and so
 $\{x\}^> \in \mathsf {P}_{\mathfrak {U}} O$
(Lemma 3). Note that by (b) we actually have
$\{x\}^> \in \mathsf {P}_{\mathfrak {U}} O$
(Lemma 3). Note that by (b) we actually have
 $x=\{x\}^> $
, although we did not need this to establish (O1
$x=\{x\}^> $
, although we did not need this to establish (O1
 ${}^{\prime }$
).
${}^{\prime }$
).
Before we prove that O is well-ordered, we will first establish the following two facts.
LetFact 1.
 $x\cap y=\mathop {\mathsf {min}}(y\setminus x)$
for any two
$x\cap y=\mathop {\mathsf {min}}(y\setminus x)$
for any two
 $\mathfrak {U}$
-ordinals x and y such that
$\mathfrak {U}$
-ordinals x and y such that
 ${y\setminus x\neq \varnothing }$
.
${y\setminus x\neq \varnothing }$
. $a\in x\cap y$
. Then
$a\in x\cap y$
. Then
 $a\notin y\setminus x$
, and hence
$a\notin y\setminus x$
, and hence
 $a\neq \mathop {\mathsf {min}}(y\setminus x)$
. By the well-ordering of y, we then get that either
$a\neq \mathop {\mathsf {min}}(y\setminus x)$
. By the well-ordering of y, we then get that either
 $a\in \mathop {\mathsf {min}}(y\setminus x)$
or
$a\in \mathop {\mathsf {min}}(y\setminus x)$
or
 $\mathop {\mathsf {min}}(y\setminus x)\in a$
. By transitivity of x and the fact that
$\mathop {\mathsf {min}}(y\setminus x)\in a$
. By transitivity of x and the fact that
 $\mathop {\mathsf {min}}(y\setminus x)\notin x$
, the second option is excluded. So
$\mathop {\mathsf {min}}(y\setminus x)\notin x$
, the second option is excluded. So
 $a\in \mathop {\mathsf {min}}(y\setminus x)$
. This shows that
$a\in \mathop {\mathsf {min}}(y\setminus x)$
. This shows that
 $x\cap y\subseteq \mathop {\mathsf {min}}(y\setminus x)$
.
$x\cap y\subseteq \mathop {\mathsf {min}}(y\setminus x)$
.
Now suppose
 $a\in \mathop {\mathsf {min}}(y\setminus x)$
. Then
$a\in \mathop {\mathsf {min}}(y\setminus x)$
. Then
 $a\in y$
by transitivity of y. If
$a\in y$
by transitivity of y. If
 $a\notin x$
, then
$a\notin x$
, then
 $a\in y\setminus x$
, which would give
$a\in y\setminus x$
, which would give
 , which is clearly impossible. So
, which is clearly impossible. So
 $a\in x$
. This proves
$a\in x$
. This proves
 $\mathop {\mathsf {min}}(y\setminus x)\subseteq x\cap y$
, and hence
$\mathop {\mathsf {min}}(y\setminus x)\subseteq x\cap y$
, and hence
 $\mathop {\mathsf {min}}(y\setminus x) = x\cap y$
.
$\mathop {\mathsf {min}}(y\setminus x) = x\cap y$
.From Fact 1 we will prove the following.
To see why this holds, considerFact 2.
 for any two
for any two
 $\mathfrak {U}$
-ordinals x and y.
$\mathfrak {U}$
-ordinals x and y. $\mathfrak {U}$
-ordinals x and y such that
$\mathfrak {U}$
-ordinals x and y such that
 $x\subseteq y$
. Then
$x\subseteq y$
. Then
 $x = x\cap y$
, and either
$x = x\cap y$
, and either
 $y\setminus x$
is empty, in which case
$y\setminus x$
is empty, in which case
 $x=y$
, or by Fact 1. The other direction follows trivially from transitivity of y.
$x=y$
, or by Fact 1. The other direction follows trivially from transitivity of y. $$ \begin{gather*} x = x\cap y = \mathop{\mathsf{min}}(y\setminus x) \in y, \end{gather*} $$
$$ \begin{gather*} x = x\cap y = \mathop{\mathsf{min}}(y\setminus x) \in y, \end{gather*} $$
We now show that O is well-ordered under the relation
 . First, we prove that O is totally ordered under
. First, we prove that O is totally ordered under
 . Consider
. Consider
 $x,y\in O$
. If
$x,y\in O$
. If
 $x\neq y$
, then either
$x\neq y$
, then either
 $x\setminus y$
or
$x\setminus y$
or
 $y\setminus x$
is nonempty. Without loss of generality, suppose that
$y\setminus x$
is nonempty. Without loss of generality, suppose that
 $y\setminus x$
is nonempty. By Fact 1,
$y\setminus x$
is nonempty. By Fact 1,
 $\mathop {\mathsf {min}}(y\setminus x)\subseteq x$
. Then, by Fact 2, either
$\mathop {\mathsf {min}}(y\setminus x)\subseteq x$
. Then, by Fact 2, either
 $\mathop {\mathsf {min}}(y\setminus x)\in x$
or
$\mathop {\mathsf {min}}(y\setminus x)\in x$
or
 $\mathop {\mathsf {min}}(y\setminus x) = x$
, and since
$\mathop {\mathsf {min}}(y\setminus x) = x$
, and since
 $\mathop {\mathsf {min}}(y\setminus x)\in y\setminus x$
, we can conclude that
$\mathop {\mathsf {min}}(y\setminus x)\in y\setminus x$
, we can conclude that
 $x=\mathop {\mathsf {min}}(y\setminus x)$
, and thus
$x=\mathop {\mathsf {min}}(y\setminus x)$
, and thus
 $x\in y$
.
$x\in y$
.Now consider a nonempty
 $Y\subseteq O$
, and any
$Y\subseteq O$
, and any
 $y\in Y$
. If
$y\in Y$
. If
 $y\cap Y=\varnothing $
, then for all
$y\cap Y=\varnothing $
, then for all
 $x\in Y$
we have
$x\in Y$
we have
 $x\notin y$
and thus
$x\notin y$
and thus
 $y=\mathop {\mathsf {min}} Y$
by total ordering. If
$y=\mathop {\mathsf {min}} Y$
by total ordering. If
 $y\cap Y\neq \varnothing $
, then
$y\cap Y\neq \varnothing $
, then
 $\mathop {\mathsf {min}}(y\cap Y)$
exists, since
$\mathop {\mathsf {min}}(y\cap Y)$
exists, since
 $y\cap Y\subseteq y$
. For all
$y\cap Y\subseteq y$
. For all
 $x\in Y\setminus y$
, it holds that
$x\in Y\setminus y$
, it holds that
 $x\notin y$
, and thus
$x\notin y$
, and thus
 $y\subseteq x$
(by total ordering and Fact 2), which in turn implies
$y\subseteq x$
(by total ordering and Fact 2), which in turn implies
 $\mathop {\mathsf {min}}(y\cap Y)\in x$
. We can conclude that
$\mathop {\mathsf {min}}(y\cap Y)\in x$
. We can conclude that
 $\mathop {\mathsf {min}}(y\cap Y)\in x$
for all
$\mathop {\mathsf {min}}(y\cap Y)\in x$
for all
 $x\in Y$
, and thus
$x\in Y$
, and thus
 $\mathop {\mathsf {min}} Y = \mathop {\mathsf {min}} (y\cap Y)$
.
$\mathop {\mathsf {min}} Y = \mathop {\mathsf {min}} (y\cap Y)$
.We will now complete the proof of (c) by showing that
 $X^<$
is nonempty for all
$X^<$
is nonempty for all
 $X\in \mathsf {P}_{\mathfrak {U}} O$
, and simultaneously prove that
$X\in \mathsf {P}_{\mathfrak {U}} O$
, and simultaneously prove that
 for all
for all
 $X\in \mathsf {P}_{\mathfrak {U}} O$
.
$X\in \mathsf {P}_{\mathfrak {U}} O$
.Consider
 $X\in \mathsf {P}_{\mathfrak {U}} O$
. By (a) and Lemma 7,
$X\in \mathsf {P}_{\mathfrak {U}} O$
. By (a) and Lemma 7,
 $X\in \mathfrak {U}$
. Then
$X\in \mathfrak {U}$
. Then
 . To show that
. To show that
 is a
is a
 $\mathfrak {U}$
-ordinal, we need to prove that it is a transitive set well-ordered under the relation
$\mathfrak {U}$
-ordinal, we need to prove that it is a transitive set well-ordered under the relation
 .
.Since each element of X is transitive,
 holds, which implies transitivity of
holds, which implies transitivity of
 :
: 
Since O is transitive by (b), and
 $X\subseteq O$
, each element of
$X\subseteq O$
, each element of
 is a
is a
 $\mathfrak {U}$
-ordinal, and thus each element of
$\mathfrak {U}$
-ordinal, and thus each element of
 is a
is a
 $\mathfrak {U}$
-ordinal. Then the fact that
$\mathfrak {U}$
-ordinal. Then the fact that
 is well-ordered under the relation
is well-ordered under the relation
 follows from the fact that O is well-ordered under the same relation, as we have already proven.
follows from the fact that O is well-ordered under the same relation, as we have already proven.Then, since
 is transitive and well-ordered under
is transitive and well-ordered under
 , we have that
, we have that
 is a
is a
 $\mathfrak {U}$
-ordinal.
$\mathfrak {U}$
-ordinal.Now, let us remark that for any
 $X\in \mathsf {P}_{\mathfrak {U}} O$
,
$X\in \mathsf {P}_{\mathfrak {U}} O$
, 
Notice that
 , and consider any
, and consider any
 $y\in X^<$
. Then
$y\in X^<$
. Then
 $X\subseteq y$
, and it is not hard to see that
$X\subseteq y$
, and it is not hard to see that
 , since
, since
 by transitivity of y. Then, by Fact 2,
by transitivity of y. Then, by Fact 2,
 , and so
, and so 
-
Step 2. We prove that if (a)–(c) hold, then O is the set of all
![]() $\mathfrak {U}$
-ordinals.
$\mathfrak {U}$
-ordinals.
Let O be any set satisfying (a)–(c).
First we prove that every element of O is a
![]() $\mathfrak {U}$
-ordinal, i.e., a transitive element of
$\mathfrak {U}$
-ordinal, i.e., a transitive element of
![]() $\mathfrak {U}$
that is well-ordered by the relation
$\mathfrak {U}$
that is well-ordered by the relation
![]() .
.
Let
![]() $x\in O$
. By (c), the set O is ordered under the relation
$x\in O$
. By (c), the set O is ordered under the relation
![]() . In this ordered set,
. In this ordered set,
By (b),
![]() $x\subseteq O$
, and so
$x\subseteq O$
, and so
![]() $x = \{x\}^> $
. By (a) and (c),
$x = \{x\}^> $
. By (a) and (c),
![]() $x\in \mathfrak {U}$
. Furthermore, for any
$x\in \mathfrak {U}$
. Furthermore, for any
![]() $y\in x$
, the following holds:
$y\in x$
, the following holds:
This shows that x is transitive.
Since O is well-ordered under
![]() (by (c) and Theorem 11) and
(by (c) and Theorem 11) and
![]() $x\subseteq O$
, we know x is also well-ordered under the same relation. Thus, every element of O is a
$x\subseteq O$
, we know x is also well-ordered under the same relation. Thus, every element of O is a
![]() $\mathfrak {U}$
-ordinal.
$\mathfrak {U}$
-ordinal.
Now we need to establish that every
![]() $\mathfrak {U}$
-ordinal is in O. We already proved that the set
$\mathfrak {U}$
-ordinal is in O. We already proved that the set
![]() $\mathcal {O}$
of all
$\mathcal {O}$
of all
![]() $\mathfrak {U}$
-ordinals is an ordinal system, and since O is a set of
$\mathfrak {U}$
-ordinals is an ordinal system, and since O is a set of
![]() $\mathfrak {U}$
-ordinals,
$\mathfrak {U}$
-ordinals,
![]() $O\subseteq \mathcal {O}$
. The equality
$O\subseteq \mathcal {O}$
. The equality
![]() $O=\mathcal {O}$
then follows from Corollary 15.⊣
$O=\mathcal {O}$
then follows from Corollary 15.⊣
5 A Dedekind-style axiomatization
A limit-successor system is a triple
![]() $X=(X,L,s)$
, where X is a set, L is a partial function
$X=(X,L,s)$
, where X is a set, L is a partial function
![]() $L\colon \mathsf {P} X\to X$
called the limit function and s is a function
$L\colon \mathsf {P} X\to X$
called the limit function and s is a function
![]() $s\colon X\to X$
called the successor function. A successor-closed subset of a limit-successor system X is a subset I of X such that
$s\colon X\to X$
called the successor function. A successor-closed subset of a limit-successor system X is a subset I of X such that
![]() $sI\subseteq I$
. For a subset
$sI\subseteq I$
. For a subset
![]() $I\subseteq X$
, write
$I\subseteq X$
, write
![]() $s^{-1}I$
to denote
$s^{-1}I$
to denote
and
![]() $L^{-1}I$
to denote
$L^{-1}I$
to denote
A subset
![]() $I\subseteq X$
is said to be closed when
$I\subseteq X$
is said to be closed when
It is not difficult to see that closed subsets form a topology on X; in fact, an Alexandrov topology (arbitrary unions of closed subset are closed). We denote the closure of a subset I in this topology by
![]() $\overline {I}$
. Recall that the corresponding ‘specialization preorder’ given by
$\overline {I}$
. Recall that the corresponding ‘specialization preorder’ given by
is a preorder (as it is for any Alexandrov topology) and that
![]() $x\in \overline {I}$
if and only if
$x\in \overline {I}$
if and only if
![]() $x\leqslant y$
for some
$x\leqslant y$
for some
![]() $y\in I$
.
$y\in I$
.
We abbreviate the operator
![]() $s^{-1}$
composed with itself m times as
$s^{-1}$
composed with itself m times as
![]() $s^{-m}$
, with the
$s^{-m}$
, with the
![]() $m=0$
case giving the identity operator. We write
$m=0$
case giving the identity operator. We write
![]() $ s^{-\infty }$
for the operator defined by
$ s^{-\infty }$
for the operator defined by
and
for the operator
. One can show that the closure of a subset
![]() $I\subseteq X$
can be computed as
$I\subseteq X$
can be computed as
This means that the specialization preorder ‘breaks up’ into two relations
![]() $\leqslant _s$
and
$\leqslant _s$
and
![]() $\prec _L$
, each determined by s and L alone, as explained in what follows. These relations are defined by:
$\prec _L$
, each determined by s and L alone, as explained in what follows. These relations are defined by:

We then have
![]() $x\leqslant y$
if and only if
$x\leqslant y$
if and only if
for some
![]() $z_0,\ldots ,z_{2k}\in X$
, where k can be any natural number
$z_0,\ldots ,z_{2k}\in X$
, where k can be any natural number
![]() $k\geqslant 0$
. Note that
$k\geqslant 0$
. Note that
![]() $\leqslant _s$
is both reflexive and transitive, although the same cannot be claimed for
$\leqslant _s$
is both reflexive and transitive, although the same cannot be claimed for
![]() $\prec _L$
.
$\prec _L$
.
Definition 18. Given a universe
![]() $\mathfrak {U}$
, a
$\mathfrak {U}$
, a
![]() $\mathfrak {U}$
-counting system is a limit-successor system
$\mathfrak {U}$
-counting system is a limit-successor system
![]() $(X,L,s)$
satisfying the following conditions:
$(X,L,s)$
satisfying the following conditions:
-
(C1) The domain of L is the set of all successor-closed subsets
 $I\in \mathsf {P}_{\mathfrak {U}} X$
.
$I\in \mathsf {P}_{\mathfrak {U}} X$
. -
(C2) If I and J belong to the domain of L and
 $\overline {I}=\overline {J}$
, then
$\overline {I}=\overline {J}$
, then
 $L(I{\kern-0.5pt})=L(J{\kern-0.5pt})$
.
$L(I{\kern-0.5pt})=L(J{\kern-0.5pt})$
.
The structure above is the one that will be used for formulating the universal property of an ordinal system at the end of this section. Before that, we give a characterization of ordinal systems as counting systems having further internal properties.
Lemma 19. Let
![]() $\mathfrak {U}$
be a universe and let
$\mathfrak {U}$
be a universe and let
![]() $(X,L,s)$
be a
$(X,L,s)$
be a
![]() $\mathfrak {U}$
-counting system. Then
$\mathfrak {U}$
-counting system. Then
![]() $\prec _L$
is transitive and furthermore,
$\prec _L$
is transitive and furthermore,
for all
![]() $x,y,z\in X$
.
$x,y,z\in X$
.
Proof. To prove transitivity of
![]() $\prec _L$
, suppose
$\prec _L$
, suppose
![]() $x\prec _L y$
and
$x\prec _L y$
and
![]() $y\prec _L z$
. Then
$y\prec _L z$
. Then
![]() $x\in I$
,
$x\in I$
,
![]() $L(I{\kern-0.5pt})=y$
,
$L(I{\kern-0.5pt})=y$
,
![]() $y\in J$
and
$y\in J$
and
![]() $L(J{\kern-0.5pt})=z$
for some successor-closed
$L(J{\kern-0.5pt})=z$
for some successor-closed
![]() $I,J\in \mathsf {P}_{\mathfrak {U}}X$
. Then the union
$I,J\in \mathsf {P}_{\mathfrak {U}}X$
. Then the union
![]() (Lemma 4) is also successor-closed, and hence it belongs to the domain of L by (C1). Since
(Lemma 4) is also successor-closed, and hence it belongs to the domain of L by (C1). Since
![]() $L(I{\kern-0.5pt})\in J$
, we get that
$L(I{\kern-0.5pt})\in J$
, we get that
![]() $I\subseteq \overline {J}$
. This implies that
$I\subseteq \overline {J}$
. This implies that
![]() . By (C2),
. By (C2),
![]() . Having
. Having
![]() and
and
![]() means that
means that
![]() $x\prec _L z$
. This completes the proof of transitivity.
$x\prec _L z$
. This completes the proof of transitivity.
To prove the second property, suppose
![]() $x\leqslant _s y\prec _L z$
. Then
$x\leqslant _s y\prec _L z$
. Then
![]() $s^{m}(x)=y$
and
$s^{m}(x)=y$
and
![]() $y\in J$
where
$y\in J$
where
![]() $L(J{\kern-0.5pt})=z$
, for some
$L(J{\kern-0.5pt})=z$
, for some
![]() $m\in \mathbb {N}$
and some successor-closed
$m\in \mathbb {N}$
and some successor-closed
![]() $J\in \mathsf {P}_{\mathfrak {U}} X$
. Here we also expand J, this time adding to it all elements of the form
$J\in \mathsf {P}_{\mathfrak {U}} X$
. Here we also expand J, this time adding to it all elements of the form
![]() $s^{k}(x)$
, where
$s^{k}(x)$
, where
![]() $k\in \{0,\ldots ,m-1\}$
. The resulting set
$k\in \{0,\ldots ,m-1\}$
. The resulting set
is clearly successor-closed and belongs to
![]() $\mathsf {P}_{\mathfrak {U}} X$
(Lemmas 2 and 4). Then, since
$\mathsf {P}_{\mathfrak {U}} X$
(Lemmas 2 and 4). Then, since
![]() $\overline {K}=\overline {J}$
, we get that
$\overline {K}=\overline {J}$
, we get that
![]() $L(K)=L(J{\kern-0.5pt})$
by (C2). This implies
$L(K)=L(J{\kern-0.5pt})$
by (C2). This implies
![]() $x\prec _L z$
.⊣
$x\prec _L z$
.⊣
This lemma gives that in a
![]() $\mathfrak {U}$
-counting system
$\mathfrak {U}$
-counting system
![]() $(X,L,s)$
, for any
$(X,L,s)$
, for any
![]() $x,z\in X$
we have
$x,z\in X$
we have
as a result of which the previous computation of the closure of a subset
![]() $I\subseteq X$
simplifies to
$I\subseteq X$
simplifies to
Note that
![]() $x\leqslant z$
now intuitively means that z is a finite successor of x, or z is a finite successor of the limit of a set containing x. Using this characterization of
$x\leqslant z$
now intuitively means that z is a finite successor of x, or z is a finite successor of the limit of a set containing x. Using this characterization of
![]() $\leqslant $
, it is also easy to confirm the following two facts:
$\leqslant $
, it is also easy to confirm the following two facts:
-
• s is increasing under
 $\leqslant $
$\leqslant $
-
•
 $x<y \Rightarrow s(x)\leqslant y$
, for all
$x<y \Rightarrow s(x)\leqslant y$
, for all
 $x,y\in X$
.
$x,y\in X$
.
Theorem 20. The specialization preorder of a
![]() $\mathfrak {U}$
-counting system
$\mathfrak {U}$
-counting system
![]() $(X,L,s)$
makes X an ordinal system relative to
$(X,L,s)$
makes X an ordinal system relative to
![]() $\mathfrak {U}$
, provided the following conditions hold:
$\mathfrak {U}$
, provided the following conditions hold:
-
(C3)
 $s^{-1}\{L(I{\kern-0.5pt})\}=\varnothing =I\cap \{s(L(I{\kern-0.5pt}))\}$
for all I such that
$s^{-1}\{L(I{\kern-0.5pt})\}=\varnothing =I\cap \{s(L(I{\kern-0.5pt}))\}$
for all I such that
 $L(I{\kern-0.5pt})$
is defined.
$L(I{\kern-0.5pt})$
is defined. -
(C4) s is injective and L has the property that if
 $L(I{\kern-0.5pt})=L(J{\kern-0.5pt})$
then
$L(I{\kern-0.5pt})=L(J{\kern-0.5pt})$
then
 $\overline {I}=\overline {J}$
.
$\overline {I}=\overline {J}$
. -
(C5)
 $J=X$
for any successor-closed set J having the property that
$J=X$
for any successor-closed set J having the property that
 $I\subseteq J\Rightarrow L(I{\kern-0.5pt})\in J$
every time
$I\subseteq J\Rightarrow L(I{\kern-0.5pt})\in J$
every time
 $L(I{\kern-0.5pt})$
is defined.
$L(I{\kern-0.5pt})$
is defined.
When these conditions hold, s is the successor function of the ordinal system and
![]() whenever
whenever
![]() $L(I{\kern-0.5pt})$
is defined; moreover, the limit ordinals are exactly the elements of X of the form
$L(I{\kern-0.5pt})$
is defined; moreover, the limit ordinals are exactly the elements of X of the form
![]() $L(I{\kern-0.5pt})$
. Furthermore, the closure of
$L(I{\kern-0.5pt})$
. Furthermore, the closure of
![]() $I\in \mathsf {P}_{\mathfrak {U}} X$
is given by
$I\in \mathsf {P}_{\mathfrak {U}} X$
is given by
![]() . Finally, any ordinal system relative to
. Finally, any ordinal system relative to
![]() $\mathfrak {U}$
arises this way from a (unique)
$\mathfrak {U}$
arises this way from a (unique)
![]() $\mathfrak {U}$
-counting system satisfying (C3–5).
$\mathfrak {U}$
-counting system satisfying (C3–5).
Before proving the theorem, let us illustrate axioms (C1–5) in the case when
![]() $\mathfrak {U}$
is the universe of hereditarily finite sets. Then L is only defined on finite successor-closed sets. Injectivity of s in (C4) forces every element x of such set to have the property
$\mathfrak {U}$
is the universe of hereditarily finite sets. Then L is only defined on finite successor-closed sets. Injectivity of s in (C4) forces every element x of such set to have the property
![]() $\exists _{m\in \mathbb {N}\setminus \{0\}}[s^m(x)=x]$
. At the same time, by (C3), such x cannot lie in the image of L. So
$\exists _{m\in \mathbb {N}\setminus \{0\}}[s^m(x)=x]$
. At the same time, by (C3), such x cannot lie in the image of L. So
has the second property in (C5). Moreover, by injectivity of s again, J is also successor-closed. Then, by (C5),
![]() $J=X$
and so L can only be defined on the empty set. With this provision, the triple
$J=X$
and so L can only be defined on the empty set. With this provision, the triple
![]() $(X,L,s)$
becomes a triple
$(X,L,s)$
becomes a triple
![]() $(X,0,s)$
where
$(X,0,s)$
where
![]() $0$
is the unique element in the image of L,
$0$
is the unique element in the image of L,
![]() $0=L(\varnothing )$
. The axioms (C1–2) then trivially hold, while (C3–5) take the form of the axioms of Dedekind for a natural number system:
$0=L(\varnothing )$
. The axioms (C1–2) then trivially hold, while (C3–5) take the form of the axioms of Dedekind for a natural number system:
-
• The first equality in (C3) states that
 $0$
does not belong to the image of s, while the second equality holds trivially.
$0$
does not belong to the image of s, while the second equality holds trivially. -
• (C4) just states that s is injective.
-
• (C5) becomes the usual principle of mathematical induction.
Proof of Theorem 20. Suppose conditions (C1–5) hold.
Step 1. As a first step, we prove that the specialization preorder is antisymmetric, i.e., that it is a partial order.
For this, we first show that
![]() $\prec _L$
is ‘antireflexive’: it is impossible to have
$\prec _L$
is ‘antireflexive’: it is impossible to have
![]() $x\prec _L x$
. Indeed, suppose
$x\prec _L x$
. Indeed, suppose
![]() $x\in I$
and
$x\in I$
and
![]() $L(I{\kern-0.5pt})=x$
. Since I is successor-closed by (C1),
$L(I{\kern-0.5pt})=x$
. Since I is successor-closed by (C1),
![]() $s(x)\in I$
. But then
$s(x)\in I$
. But then
![]() $s(x)\in I\cap \{s(L(I{\kern-0.5pt}))\}$
, which is impossible by (C3).
$s(x)\in I\cap \{s(L(I{\kern-0.5pt}))\}$
, which is impossible by (C3).
Next, we show antisymmetry of
![]() $\leqslant _s$
. Suppose
$\leqslant _s$
. Suppose
![]() $x\leqslant _s z\leqslant _s x$
and
$x\leqslant _s z\leqslant _s x$
and
![]() $x\neq z$
. Then we get that
$x\neq z$
. Then we get that
![]() $s^k(x)=x$
for
$s^k(x)=x$
for
![]() $k>1$
. We will now show that this is not possible. In fact, we establish a slightly stronger property, which will be useful later on as well:
$k>1$
. We will now show that this is not possible. In fact, we establish a slightly stronger property, which will be useful later on as well:
Property 1.
![]() $s^k(x)\neq x$
for all
$s^k(x)\neq x$
for all
![]() $x\in X$
and all natural numbers
$x\in X$
and all natural numbers
![]() $k>0$
.
$k>0$
.
Actually, we have already established this property in the remark after the theorem. Here is a more detailed argument. Consider the set
We will use (C5) to show that
![]() $J=X$
.
$J=X$
.
First, we show that J is successor-closed. Let
![]() $y\in J$
, and suppose
$y\in J$
, and suppose
![]() $s^k(s(y)) = s(y)$
for some
$s^k(s(y)) = s(y)$
for some
![]() $k>0$
. Then, by injectivity of s (which is required in (C4)),
$k>0$
. Then, by injectivity of s (which is required in (C4)),
![]() $s^{k-1}(s(y)) = y$
, which is impossible. So
$s^{k-1}(s(y)) = y$
, which is impossible. So
![]() $s(y)\in J$
, showing that J is successor-closed.
$s(y)\in J$
, showing that J is successor-closed.
Now let
![]() $I\in \mathsf {P}_{\mathfrak {U}} X$
be a successor-closed subset of J (by (C1), I is such if and only if
$I\in \mathsf {P}_{\mathfrak {U}} X$
be a successor-closed subset of J (by (C1), I is such if and only if
![]() $L(I{\kern-0.5pt})$
is defined). Then
$L(I{\kern-0.5pt})$
is defined). Then
![]() $L(I{\kern-0.5pt})\neq s^k(L(I{\kern-0.5pt}))$
for all
$L(I{\kern-0.5pt})\neq s^k(L(I{\kern-0.5pt}))$
for all
![]() $k>0$
by the first equality in (C3). Thus
$k>0$
by the first equality in (C3). Thus
![]() $L(I{\kern-0.5pt})\in J$
, and we can apply (C5) to get
$L(I{\kern-0.5pt})\in J$
, and we can apply (C5) to get
![]() $J=X$
, as desired. Antisymmetry of
$J=X$
, as desired. Antisymmetry of
![]() $\leqslant _s$
has thus been established.
$\leqslant _s$
has thus been established.
We are now ready to prove the antisymmetry of
![]() $\leqslant $
. Suppose
$\leqslant $
. Suppose
![]() $x\leqslant z$
and
$x\leqslant z$
and
![]() $z\leqslant x$
. There are four cases to consider:
$z\leqslant x$
. There are four cases to consider:
Case 1. (
 $x\leqslant _s z\leqslant _s x$
)
$x\leqslant _s z\leqslant _s x$
)
Then
![]() $x=z$
by antisymmetry of
$x=z$
by antisymmetry of
![]() $\leqslant _s$
.
$\leqslant _s$
.
Case 2. (
 $x\prec _L y\leqslant _s z\leqslant _s x$
for some y)
$x\prec _L y\leqslant _s z\leqslant _s x$
for some y)
Then
 $$\begin{align*}\kern3pc &y\leqslant_s z\leqslant_s x \prec_L y \nonumber\\ \kern86pt\quad \Rightarrow \quad &y\leqslant_s x \prec_L y \kern85pt(\mathrm{by\ transitivity\ of} \leqslant_s)\\ \kern86pt\quad \Rightarrow \quad &y \prec_L y, \kern133pt(\mathrm{by\ Lemma\ 19}) \end{align*} $$
$$\begin{align*}\kern3pc &y\leqslant_s z\leqslant_s x \prec_L y \nonumber\\ \kern86pt\quad \Rightarrow \quad &y\leqslant_s x \prec_L y \kern85pt(\mathrm{by\ transitivity\ of} \leqslant_s)\\ \kern86pt\quad \Rightarrow \quad &y \prec_L y, \kern133pt(\mathrm{by\ Lemma\ 19}) \end{align*} $$
which we have shown to be impossible.
Case 3. (
 $x\leqslant _s z\prec _L y\leqslant _s x$
for some y)
$x\leqslant _s z\prec _L y\leqslant _s x$
for some y)
Then, similarly, we get the impossible
 $$ \begin{align*} &y\leqslant_s x\leqslant_s z \prec_L y \nonumber\\ \kern86pt\quad \Rightarrow \quad &y\leqslant_s z \prec_L y \kern85.5pt(\mathrm{by\ transitivity\ of} \leqslant_s)\\ \kern86pt\quad \Rightarrow \quad &y \prec_L y. \kern133.5pt(\mathrm{by\ Lemma\ 19}) \end{align*} $$
$$ \begin{align*} &y\leqslant_s x\leqslant_s z \prec_L y \nonumber\\ \kern86pt\quad \Rightarrow \quad &y\leqslant_s z \prec_L y \kern85.5pt(\mathrm{by\ transitivity\ of} \leqslant_s)\\ \kern86pt\quad \Rightarrow \quad &y \prec_L y. \kern133.5pt(\mathrm{by\ Lemma\ 19}) \end{align*} $$
Case 4. (
 $x\prec _L y\leqslant _s z\prec _L y'\leqslant _s x$
for some
$x\prec _L y\leqslant _s z\prec _L y'\leqslant _s x$
for some
 $y,y'$
)
$y,y'$
)
In this case, too, we get the impossible
 $$ \begin{align*} &y\leqslant_s z\prec_L y' \leqslant_s x\prec_L y \nonumber\\ \kern60pt\quad \Rightarrow \quad &y\prec_L y'\prec_L y \kern134pt(\mathrm{by\ Lemma\ 19})\\\kern60pt\quad \Rightarrow \quad &y \prec_L y. \kern60pt(\mathrm{by\ transitivity\ of} \prec_{L} \mathrm{from\ Lemma\ 19}) \end{align*} $$
$$ \begin{align*} &y\leqslant_s z\prec_L y' \leqslant_s x\prec_L y \nonumber\\ \kern60pt\quad \Rightarrow \quad &y\prec_L y'\prec_L y \kern134pt(\mathrm{by\ Lemma\ 19})\\\kern60pt\quad \Rightarrow \quad &y \prec_L y. \kern60pt(\mathrm{by\ transitivity\ of} \prec_{L} \mathrm{from\ Lemma\ 19}) \end{align*} $$
We have thus shown that the specialization preorder is antisymmetric. We will now establish the following property, which will be useful later on.
Property 2. If
![]() $x<s(y)$
then
$x<s(y)$
then
![]() $x\leqslant y$
, for all
$x\leqslant y$
, for all
![]() $x,y\in X$
.
$x,y\in X$
.
Suppose
![]() $x<s(y)$
. Again, we have two cases:
$x<s(y)$
. Again, we have two cases:
Case 1. (
 $x\leqslant _s s(y)$
)
$x\leqslant _s s(y)$
)
This, together with
![]() $x\neq s(y)$
, gives
$x\neq s(y)$
, gives
![]() $x\leqslant y$
by injectivity of s from (C4).
$x\leqslant y$
by injectivity of s from (C4).
Case 2. (
 $x\prec _L x'\leqslant _s s(y)$
for some
$x\prec _L x'\leqslant _s s(y)$
for some
 $x'\in X$
)
$x'\in X$
)
Since
![]() $x'\neq s(y)$
by the first equality in (C3), by injectivity of s (from (C4)), we must have
$x'\neq s(y)$
by the first equality in (C3), by injectivity of s (from (C4)), we must have
![]() $x'\leqslant _s y$
. This gives us
$x'\leqslant _s y$
. This gives us
![]() $x\leqslant y$
.
$x\leqslant y$
.
We get
![]() $x\leqslant y$
in both cases.
$x\leqslant y$
in both cases.
Step 2. We prove that the specialization preorder is a total order.
We will prove this by simultaneously establishing the following:
Property 3. Let
![]() $y\in X$
, and let
$y\in X$
, and let
![]() $I\subseteq X$
. If
$I\subseteq X$
. If
![]() $x<y$
for all
$x<y$
for all
![]() $x\in I$
and
$x\in I$
and
![]() $L(I{\kern-0.5pt})$
is defined, then
$L(I{\kern-0.5pt})$
is defined, then
![]() $L(I{\kern-0.5pt})\leqslant y$
.
$L(I{\kern-0.5pt})\leqslant y$
.
Let
We will use (C5) to show that
![]() $J=X$
. For this, we first prove that J is successor-closed. Let
$J=X$
. For this, we first prove that J is successor-closed. Let
![]() $x\in J$
, and consider any
$x\in J$
, and consider any
![]() $y\in X$
. Since
$y\in X$
. Since
![]() $x\leqslant s(x)$
, if
$x\leqslant s(x)$
, if
![]() $y\leqslant x$
, then
$y\leqslant x$
, then
![]() $y\leqslant s(x)$
. If
$y\leqslant s(x)$
. If
![]() $x<y$
, then
$x<y$
, then
![]() $s(x)\leqslant y$
, as remarked after Lemma 19. This proves that J is successor-closed.
$s(x)\leqslant y$
, as remarked after Lemma 19. This proves that J is successor-closed.
Now consider
![]() $L(I{\kern-0.5pt})$
, where
$L(I{\kern-0.5pt})$
, where
![]() $I\subseteq J$
. To prove that
$I\subseteq J$
. To prove that
![]() $L(I{\kern-0.5pt})\in J$
, we proceed as follows. Let
$L(I{\kern-0.5pt})\in J$
, we proceed as follows. Let
![]() $x\in X$
. If
$x\in X$
. If
![]() $x\leqslant y$
for at least one
$x\leqslant y$
for at least one
![]() $y\in I$
, then
$y\in I$
, then
![]() $x\leqslant L(I{\kern-0.5pt})$
, since
$x\leqslant L(I{\kern-0.5pt})$
, since
![]() $y\prec _L L(I{\kern-0.5pt})$
. Thus, it suffices to prove that the set
$y\prec _L L(I{\kern-0.5pt})$
. Thus, it suffices to prove that the set
is the entire
![]() $K_I=X$
. This we prove using (C5).
$K_I=X$
. This we prove using (C5).
First, we show that
![]() $K_I$
is successor-closed. Suppose
$K_I$
is successor-closed. Suppose
![]() $x\in K_I$
. If
$x\in K_I$
. If
![]() $y<s(x)$
for all
$y<s(x)$
for all
![]() $y\in I$
, then by Property 2,
$y\in I$
, then by Property 2,
![]() $y\leqslant x$
for all
$y\leqslant x$
for all
![]() $y\in I$
. If
$y\in I$
. If
![]() $y=x$
for some
$y=x$
for some
![]() $y\in I$
, then
$y\in I$
, then
![]() $x\in I$
, and, since I is successor-closed by (C1), we will have
$x\in I$
, and, since I is successor-closed by (C1), we will have
![]() $s(x)\in I$
, which will violate the assumption that
$s(x)\in I$
, which will violate the assumption that
![]() $y<s(x)$
for all
$y<s(x)$
for all
![]() $y\in I$
. So we get that
$y\in I$
. So we get that
![]() $y<x$
for all
$y<x$
for all
![]() $y\in I$
. Then
$y\in I$
. Then
![]() $L(I{\kern-0.5pt})\leqslant x$
, since
$L(I{\kern-0.5pt})\leqslant x$
, since
![]() $x\in K_I$
. This implies
$x\in K_I$
. This implies
![]() $L(I{\kern-0.5pt})\leqslant s(x)$
, thus proving that
$L(I{\kern-0.5pt})\leqslant s(x)$
, thus proving that
![]() $K_I$
is successor-closed.
$K_I$
is successor-closed.
Now let
![]() $H\subseteq K_I$
be such that
$H\subseteq K_I$
be such that
![]() $L(H)$
is defined. Suppose
$L(H)$
is defined. Suppose
![]() $y<L(H) $
for all
$y<L(H) $
for all
![]() $y\in I$
. From the first equality in (C3), we get that
$y\in I$
. From the first equality in (C3), we get that
![]() $y\prec _L L(H) $
for each
$y\prec _L L(H) $
for each
![]() $y\in I$
. So for each
$y\in I$
. So for each
![]() $y\in I$
, there exists
$y\in I$
, there exists
![]() $G_y$
such that
$G_y$
such that
![]() $y\in G_y$
and
$y\in G_y$
and
![]() $L(G_y)=L(H) $
. This implies that
$L(G_y)=L(H) $
. This implies that
![]() $\overline {G_y}= \overline {H}$
for each
$\overline {G_y}= \overline {H}$
for each
![]() $y\in I$
(by (C4)), and so
$y\in I$
(by (C4)), and so
![]() $I\subseteq \overline {H}$
. Since
$I\subseteq \overline {H}$
. Since
![]() $I\subseteq J$
, each element of H is comparable with each element of I. We consider two cases.
$I\subseteq J$
, each element of H is comparable with each element of I. We consider two cases.
Case 1. (for every
 $h\in H$
, there exists
$h\in H$
, there exists
 $y\in I$
such that
$y\in I$
such that
 $h\leqslant y$
)
$h\leqslant y$
)
Then
![]() $H\subseteq \overline {I}$
. This would then give
$H\subseteq \overline {I}$
. This would then give
![]() $\overline {I}=\overline {H}$
, and so by (C2),
$\overline {I}=\overline {H}$
, and so by (C2),
![]() $L(I{\kern-0.5pt})=L(H) $
, showing that
$L(I{\kern-0.5pt})=L(H) $
, showing that
![]() $L(I{\kern-0.5pt})\leqslant L(H) $
, as desired.
$L(I{\kern-0.5pt})\leqslant L(H) $
, as desired.
Case 2. (there exists
 $h\in H$
such that
$h\in H$
such that
 $y<h$
for every
$y<h$
for every
 $y\in I$
)
$y\in I$
)
Since
![]() $H\subseteq K_I$
, this gives us
$H\subseteq K_I$
, this gives us
![]() $L(I{\kern-0.5pt})\leqslant h$
. This, together with
$L(I{\kern-0.5pt})\leqslant h$
. This, together with
![]() $h\prec _L L(H)$
, will give
$h\prec _L L(H)$
, will give
![]() $L(I{\kern-0.5pt})\leqslant L(H)$
.
$L(I{\kern-0.5pt})\leqslant L(H)$
.
In both cases,
![]() $L(I{\kern-0.5pt})\leqslant L(H)$
. We have thus shown that
$L(I{\kern-0.5pt})\leqslant L(H)$
. We have thus shown that
![]() $K_I$
has the required properties for us to apply (C5) to conclude that
$K_I$
has the required properties for us to apply (C5) to conclude that
![]() $K_I=X$
. This, then, shows that
$K_I=X$
. This, then, shows that
![]() $L(I{\kern-0.5pt})\in J$
, and so J has the required properties to conclude that
$L(I{\kern-0.5pt})\in J$
, and so J has the required properties to conclude that
![]() $J=X$
. The proof that the specialization preorder is a total order is now complete. At the same time, since
$J=X$
. The proof that the specialization preorder is a total order is now complete. At the same time, since
![]() $J=X$
, and for each
$J=X$
, and for each
![]() $I\subseteq J$
such that
$I\subseteq J$
such that
![]() $L(I{\kern-0.5pt})$
is defined,
$L(I{\kern-0.5pt})$
is defined,
![]() $K_I=X$
, we have also established Property 3.
$K_I=X$
, we have also established Property 3.
Step 3. We now show that
![]() whenever
whenever
![]() $L(I{\kern-0.5pt})$
is defined, and that
$L(I{\kern-0.5pt})$
is defined, and that
![]() $s(x)=x^+$
for all
$s(x)=x^+$
for all
![]() $x\in X$
.
$x\in X$
.
Properties 1 and 3 show that
![]() $L(I{\kern-0.5pt})$
is the join of I for any I such that
$L(I{\kern-0.5pt})$
is the join of I for any I such that
![]() $L(I{\kern-0.5pt})$
is defined. Indeed, if
$L(I{\kern-0.5pt})$
is defined. Indeed, if
![]() $x\leqslant y$
for all
$x\leqslant y$
for all
![]() $x\in I$
, then for each
$x\in I$
, then for each
![]() $x\in I$
, we also have
$x\in I$
, we also have
![]() $s(x)\leqslant y$
. Since
$s(x)\leqslant y$
. Since
![]() $x<s(x)$
, as clearly
$x<s(x)$
, as clearly
![]() $x\leqslant s(x)$
and by Property 1,
$x\leqslant s(x)$
and by Property 1,
![]() $x\neq s(x)$
, we get that
$x\neq s(x)$
, we get that
![]() $x<y$
for all
$x<y$
for all
![]() $x\in I$
. Then, by Property 3,
$x\in I$
. Then, by Property 3,
![]() $L(I{\kern-0.5pt})\leqslant y$
, thus showing that
$L(I{\kern-0.5pt})\leqslant y$
, thus showing that
![]() $L(I{\kern-0.5pt})$
is a join of I.
$L(I{\kern-0.5pt})$
is a join of I.
Furthermore, when
![]() $L(I{\kern-0.5pt})$
is defined, I is successor-closed and so it cannot have a largest element, by Property 1. Then the join
$L(I{\kern-0.5pt})$
is defined, I is successor-closed and so it cannot have a largest element, by Property 1. Then the join
![]() $L(I{\kern-0.5pt})$
of I must also be the incremented join of I (Lemma 9).
$L(I{\kern-0.5pt})$
of I must also be the incremented join of I (Lemma 9).
Finally, the property
![]() $x<s(x)$
, together with the fact that
$x<s(x)$
, together with the fact that
![]() $s(x)\leqslant y$
whenever
$s(x)\leqslant y$
whenever
![]() $x< y$
, implies that
$x< y$
, implies that
![]() $s(x)=x^+$
for each
$s(x)=x^+$
for each
![]() $x\in X$
. Thus, once we prove that X is an ordinal system under the specialization preorder, we have that s is its successor function and L is given by the join.
$x\in X$
. Thus, once we prove that X is an ordinal system under the specialization preorder, we have that s is its successor function and L is given by the join.
Step 4. We prove that X is an ordinal system under the specialization preorder, where limit ordinals are exactly the elements of the form
![]() $L(I{\kern-0.5pt})$
.
$L(I{\kern-0.5pt})$
.
Consider the set
If
![]() $x\in J$
, then by Property 2,
$x\in J$
, then by Property 2,
![]() (Lemmas 2 and 4), and so
(Lemmas 2 and 4), and so
![]() $s(x)\in J$
. For any
$s(x)\in J$
. For any
![]() $x\in J$
, we therefore have
$x\in J$
, we therefore have
 $$ \begin{align*} \overline{\{x\}} &= \{y\in X\mid y\leqslant x\}\nonumber\\ &= \{y\in X\mid y < s(x)\} \qquad\qquad\qquad{by\ Property\ 2}\\ &= \{s(x)\}^> \in \mathsf{P}_{\mathfrak{U}} X.\nonumber \end{align*} $$
$$ \begin{align*} \overline{\{x\}} &= \{y\in X\mid y\leqslant x\}\nonumber\\ &= \{y\in X\mid y < s(x)\} \qquad\qquad\qquad{by\ Property\ 2}\\ &= \{s(x)\}^> \in \mathsf{P}_{\mathfrak{U}} X.\nonumber \end{align*} $$
Suppose
![]() $I\subseteq J$
is such that
$I\subseteq J$
is such that
![]() $L(I{\kern-0.5pt})$
is defined, and define a function
$L(I{\kern-0.5pt})$
is defined, and define a function
![]() $f\colon I\to \mathsf {P}_{\mathfrak {U}} X$
by
$f\colon I\to \mathsf {P}_{\mathfrak {U}} X$
by
![]() $f(x) = \overline {\{x\}}$
. Then, by Lemma 4,
$f(x) = \overline {\{x\}}$
. Then, by Lemma 4,
Notice that
, since
![]() $\overline {I}$
is the down-closure of I under the specialization preorder.
$\overline {I}$
is the down-closure of I under the specialization preorder.
Then, note that
holds for all
![]() $I\subseteq X$
, as is true in any Alexandrov topology, and thus
$I\subseteq X$
, as is true in any Alexandrov topology, and thus

and so
![]() $L(I{\kern-0.5pt})\in J$
. By (C5),
$L(I{\kern-0.5pt})\in J$
. By (C5),
![]() $J=X$
, and thus (O1
$J=X$
, and thus (O1
![]() ${}^{\prime }$
) holds.
${}^{\prime }$
) holds.
To prove that X is an ordinal system under the specialization preorder, it remains to show that it satisfies (O2), i.e., that for any
![]() $Y\in \mathsf {P}_{\mathfrak {U}} X$
, the incremented join of Y exists in X. If Y has a largest element, then the successor of that element is the incremented join of Y (Lemma 9). If
$Y\in \mathsf {P}_{\mathfrak {U}} X$
, the incremented join of Y exists in X. If Y has a largest element, then the successor of that element is the incremented join of Y (Lemma 9). If
![]() $\mathfrak {U}$
does not contain an infinite set, then Y is finite, and so it has a largest element.
$\mathfrak {U}$
does not contain an infinite set, then Y is finite, and so it has a largest element.
Now consider
![]() $Y\in \mathsf {P}_{\mathfrak {U}} X$
that has no largest element, with
$Y\in \mathsf {P}_{\mathfrak {U}} X$
that has no largest element, with
![]() $\mathfrak {U}$
containing an infinite set. We define:
$\mathfrak {U}$
containing an infinite set. We define:
This is, of course, the closure of Y under s. Consider a function
![]() $f\colon Y\times \mathbb {N}\to X$
defined by
$f\colon Y\times \mathbb {N}\to X$
defined by
![]() $f(x,n) = s^n(x)$
. Then, by Lemmas 5 and 6,
$f(x,n) = s^n(x)$
. Then, by Lemmas 5 and 6,
 $$ \begin{align*} s^\infty Y &= \{ s^n (x)\mid [x\in Y]\land [n\in\mathbb{N}]\}\\ &= \{ f(x,n) \mid (x,n) \in Y\times \mathbb{N} \}\\ &= f(Y\times \mathbb{N}) \in \mathsf{P}_{\mathfrak{U}} X. \end{align*} $$
$$ \begin{align*} s^\infty Y &= \{ s^n (x)\mid [x\in Y]\land [n\in\mathbb{N}]\}\\ &= \{ f(x,n) \mid (x,n) \in Y\times \mathbb{N} \}\\ &= f(Y\times \mathbb{N}) \in \mathsf{P}_{\mathfrak{U}} X. \end{align*} $$
Thus
![]() $L(s^\infty Y)$
is defined, by (C1). Since
$L(s^\infty Y)$
is defined, by (C1). Since
![]() $Y\subseteq s^\infty Y$
, it holds that
$Y\subseteq s^\infty Y$
, it holds that
![]() $y<L(s^\infty Y)$
for all
$y<L(s^\infty Y)$
for all
![]() $y\in Y$
. Let
$y\in Y$
. Let
![]() $y\in Y$
. We prove by induction on n that for each
$y\in Y$
. We prove by induction on n that for each
![]() $n\in \mathbb {N}$
, we have
$n\in \mathbb {N}$
, we have
![]() $s^n(y)<z$
for some
$s^n(y)<z$
for some
![]() $z\in Y$
.
$z\in Y$
.
Base case. If
![]() $n=0$
, this follows from the fact that Y does not have a largest element.
$n=0$
, this follows from the fact that Y does not have a largest element.
Induction step. Suppose
![]() $s^n(y)<z$
for some
$s^n(y)<z$
for some
![]() $z\in Y$
. Then
$z\in Y$
. Then
![]() $s^{n+1}(y) = s(s^n(y))\leqslant z$
. Since z cannot be the largest element of Y, we must have
$s^{n+1}(y) = s(s^n(y))\leqslant z$
. Since z cannot be the largest element of Y, we must have
![]() $z<z'$
for some
$z<z'$
for some
![]() $z'\in Y$
. Then
$z'\in Y$
. Then
![]() $s^{n+1}(y)<z'$
.
$s^{n+1}(y)<z'$
.
What we have shown implies that the incremented join
![]() $ L(s^\infty Y)$
of
$ L(s^\infty Y)$
of
![]() $s^\infty Y$
is also the incremented join of Y.
$s^\infty Y$
is also the incremented join of Y.
We have thus proven that the specialization preorder of a
![]() $\mathfrak {U}$
-counting system satisfying (C3–5) makes it an ordinal system relative to
$\mathfrak {U}$
-counting system satisfying (C3–5) makes it an ordinal system relative to
![]() $\mathfrak {U}$
, with s as its successor function, and L given equivalently by join and by incremented join. This also establishes that, if an ordinal system relative to
$\mathfrak {U}$
, with s as its successor function, and L given equivalently by join and by incremented join. This also establishes that, if an ordinal system relative to
![]() $\mathfrak {U}$
arises this way from a
$\mathfrak {U}$
arises this way from a
![]() $\mathfrak {U}$
-counting system satisfying (C3–5), then this
$\mathfrak {U}$
-counting system satisfying (C3–5), then this
![]() $\mathfrak {U}$
-counting system is unique.
$\mathfrak {U}$
-counting system is unique.
We now prove the existence of such a
![]() $\mathfrak {U}$
-counting system. Actually, before doing that, note that by (C3), no element of X of the form
$\mathfrak {U}$
-counting system. Actually, before doing that, note that by (C3), no element of X of the form
![]() $L(I{\kern-0.5pt})$
can be a successor ordinal, and so it must be a limit ordinal. Conversely, for a limit ordinal x we have
$L(I{\kern-0.5pt})$
can be a successor ordinal, and so it must be a limit ordinal. Conversely, for a limit ordinal x we have
![]() $x = L(\{x\}^>)$
(Lemma 12). This shows that limit ordinals are precisely the ordinals of the form
$x = L(\{x\}^>)$
(Lemma 12). This shows that limit ordinals are precisely the ordinals of the form
![]() $L(I{\kern-0.5pt})$
.
$L(I{\kern-0.5pt})$
.
For an ordinal system
![]() $\mathcal {O}$
relative to
$\mathcal {O}$
relative to
![]() $\mathfrak {U}$
, consider the limit-successor system
$\mathfrak {U}$
, consider the limit-successor system
![]() , where
, where
![]() is the usual join restricted to the domain required by (C1) (i.e., successor-closed elements of
is the usual join restricted to the domain required by (C1) (i.e., successor-closed elements of
![]() $\mathsf {P}_{\mathfrak {U}} X$
).
$\mathsf {P}_{\mathfrak {U}} X$
).
Step 5. We show that (C1–5) hold for the limit-successor system
![]() and that the corresponding specialization preorder matches with the order of
and that the corresponding specialization preorder matches with the order of
![]() $\mathcal {O}$
. In this step we also show that
$\mathcal {O}$
. In this step we also show that
![]() holds for each
holds for each
![]() $I\in \mathsf {P}_{\mathfrak {U}} \mathcal {O}$
.
$I\in \mathsf {P}_{\mathfrak {U}} \mathcal {O}$
.
By Theorem 13, L is indeed defined over the entire domain required in (C1). To prove (C2), first we establish that
for each
![]() $I\in \mathsf {P}_{\mathfrak {U}} \mathcal {O}$
. It is easy to see that
$I\in \mathsf {P}_{\mathfrak {U}} \mathcal {O}$
. It is easy to see that
is closed, so
. To show
, let
. We have well-ordering and hence total order by Theorem 11. Then
and so
![]() $x\leqslant y\in I$
for some y. Consider
$x\leqslant y\in I$
for some y. Consider
We consider two cases:
Case 1. (
 $y'$
is a successor ordinal)
$y'$
is a successor ordinal)
Then
![]() $y'=y'{}'{}^+$
for some ordinal
$y'=y'{}'{}^+$
for some ordinal
![]() $y'{}'$
. Since
$y'{}'$
. Since
![]() $y'\in \overline {I}$
, we must have
$y'\in \overline {I}$
, we must have
![]() $y'{}'\in \overline {I}$
. Then
$y'{}'\in \overline {I}$
. Then
![]() $y'{}'<x$
and so
$y'{}'<x$
and so
![]() $y'\leqslant x$
by (L3). This gives
$y'\leqslant x$
by (L3). This gives
![]() $x=y'$
and so
$x=y'$
and so
![]() $x\in \overline {I}$
.
$x\in \overline {I}$
.
Case 2. (
 $y'$
is a limit ordinal)
$y'$
is a limit ordinal)
Then
![]() $\{y'\}^> $
is successor-closed. Furthermore, we have
$\{y'\}^> $
is successor-closed. Furthermore, we have
By closure of
![]() $\overline {I}$
, we get
$\overline {I}$
, we get
![]() $\{y'\}^> \subseteq \overline {I}$
. Since
$\{y'\}^> \subseteq \overline {I}$
. Since
![]() $y<x$
for all
$y<x$
for all
![]() $y<y'$
, we get
$y<y'$
, we get
![]() $y'\leqslant x$
. This gives
$y'\leqslant x$
. This gives
![]() $x=y'$
and so
$x=y'$
and so
![]() $x\in \overline {I}$
.
$x\in \overline {I}$
.
We have thus established that the equality
![]() holds for each
holds for each
![]() $I\in \mathsf {P}_{\mathfrak {U}} \mathcal {O}$
. From this it follows that the specialization preorder matches with the order of
$I\in \mathsf {P}_{\mathfrak {U}} \mathcal {O}$
. From this it follows that the specialization preorder matches with the order of
![]() $\mathcal {O}$
. We then get that (C2) holds by the fact that if down-closures of two subsets of a poset are equal, then so are their joins. Thus
$\mathcal {O}$
. We then get that (C2) holds by the fact that if down-closures of two subsets of a poset are equal, then so are their joins. Thus
![]() is a
is a
![]() $\mathfrak {U}$
-counting system.
$\mathfrak {U}$
-counting system.
It remains to show that (C3–5) hold. Consider a successor-closed
![]() $I\in \mathsf {P}_{\mathfrak {U}} \mathcal {O}$
. I has no maximum element thanks to (L1) and thus,
$I\in \mathsf {P}_{\mathfrak {U}} \mathcal {O}$
. I has no maximum element thanks to (L1) and thus,
![]() by Lemma 9. By the same lemma,
by Lemma 9. By the same lemma,
![]() cannot be a successor if I has no maximum. Thus,
cannot be a successor if I has no maximum. Thus,
![]() , which is the first part of (C3). Since
, which is the first part of (C3). Since
![]() for each
for each
![]() $x\in I$
, we have that
$x\in I$
, we have that
![]() , which means the second part of (C3) also holds, i.e.,
, which means the second part of (C3) also holds, i.e.,
![]() .
.
We already know that
![]() $\_^+$
is injective, so to see that (C4) holds, consider another successor-closed
$\_^+$
is injective, so to see that (C4) holds, consider another successor-closed
![]() $J\in \mathsf {P}_{\mathfrak {U}} \mathcal {O}$
. If
$J\in \mathsf {P}_{\mathfrak {U}} \mathcal {O}$
. If
, then
Thus (C4) holds. Finally, consider a successor-closed subset J of
![]() $\mathcal {O}$
where
$\mathcal {O}$
where
for all successor-closed subsets I of J such that
![]() $I\in \mathsf {P}_{\mathfrak {U}} \mathcal {O}$
. Then
$I\in \mathsf {P}_{\mathfrak {U}} \mathcal {O}$
. Then
![]() $J=\mathcal {O}$
if it satisfies (I1) and (I2) in our formulation of transfinite induction. We check both:
$J=\mathcal {O}$
if it satisfies (I1) and (I2) in our formulation of transfinite induction. We check both:
-
I1.
 $J^+\subseteq J$
follows from the fact that J is successor-closed.
$J^+\subseteq J$
follows from the fact that J is successor-closed. -
I2. Let x be a limit ordinal such that
 $\{x\}^>\subseteq J$
. Then
$\{x\}^>\subseteq J$
. Then
 by Lemma 12.
by Lemma 12.
Since both of these conditions hold, we can conclude that
![]() $J=\mathcal {O}$
, and thus (C5) holds. This completes the proof.⊣
$J=\mathcal {O}$
, and thus (C5) holds. This completes the proof.⊣
Given two
![]() $\mathfrak {U}$
-counting systems
$\mathfrak {U}$
-counting systems
![]() $(X_1,L_1,s_1)$
and
$(X_1,L_1,s_1)$
and
![]() $(X_2,L_2,s_2)$
, a function
$(X_2,L_2,s_2)$
, a function
![]() $f\colon X_1\to X_2$
that preserves the successor function (
$f\colon X_1\to X_2$
that preserves the successor function (
![]() $fs_1=s_2f$
) automatically preserves successor-closed subsets, so for any successor-closed
$fs_1=s_2f$
) automatically preserves successor-closed subsets, so for any successor-closed
![]() $I\in \mathsf {P}_{\mathfrak {U}} X_1$
, both sides of the equality
$I\in \mathsf {P}_{\mathfrak {U}} X_1$
, both sides of the equality
are defined (Lemma 5). When this equality holds for any such I, along with f preserving successors, we say that f is a morphism of
![]() $\mathfrak {U}$
-counting systems and represent f as an arrow
$\mathfrak {U}$
-counting systems and represent f as an arrow
It is not difficult to see that
![]() $\mathfrak {U}$
-counting systems and morphisms between them form a category, under the usual composition of functions. Isomorphisms in this category are bijections between
$\mathfrak {U}$
-counting systems and morphisms between them form a category, under the usual composition of functions. Isomorphisms in this category are bijections between
![]() $\mathfrak {U}$
-counting systems which preserve both succession and limiting. Call a
$\mathfrak {U}$
-counting systems which preserve both succession and limiting. Call a
![]() $\mathfrak {U}$
-counting system an ordinal
$\mathfrak {U}$
-counting system an ordinal
![]() $\mathfrak {U}$
-counting system when conditions (C3–5) hold. Clearly, the property of being an ordinal
$\mathfrak {U}$
-counting system when conditions (C3–5) hold. Clearly, the property of being an ordinal
![]() $\mathfrak {U}$
-counting system is stable under isomorphism of
$\mathfrak {U}$
-counting system is stable under isomorphism of
![]() $\mathfrak {U}$
-counting systems. By Theorems 17 and 20, an ordinal
$\mathfrak {U}$
-counting systems. By Theorems 17 and 20, an ordinal
![]() $\mathfrak {U}$
-counting system exists and is given by the
$\mathfrak {U}$
-counting system exists and is given by the
![]() $\mathfrak {U}$
-ordinals. We will now see that ordinal
$\mathfrak {U}$
-ordinals. We will now see that ordinal
![]() $\mathfrak {U}$
-counting systems are precisely the initial objects in the category of
$\mathfrak {U}$
-counting systems are precisely the initial objects in the category of
![]() $\mathfrak {U}$
-counting systems.
$\mathfrak {U}$
-counting systems.
Theorem 21. For any universe
![]() $\mathfrak {U}$
, a
$\mathfrak {U}$
, a
![]() $\mathfrak {U}$
-counting system is an initial object in the category of
$\mathfrak {U}$
-counting system is an initial object in the category of
![]() $\mathfrak {U}$
-counting systems if and only if it is an ordinal
$\mathfrak {U}$
-counting systems if and only if it is an ordinal
![]() $\mathfrak {U}$
-counting system.
$\mathfrak {U}$
-counting system.
Proof. Since we know that an ordinal
![]() $\mathfrak {U}$
-counting system exists (Theorem 17) and that the property of being an ordinal
$\mathfrak {U}$
-counting system exists (Theorem 17) and that the property of being an ordinal
![]() $\mathfrak {U}$
-counting system is stable under isomorphism, it suffices to show that any ordinal
$\mathfrak {U}$
-counting system is stable under isomorphism, it suffices to show that any ordinal
![]() $\mathfrak {U}$
-counting system is an initial object in the category of
$\mathfrak {U}$
-counting system is an initial object in the category of
![]() $\mathfrak {U}$
-counting systems. By Theorem 20, an ordinal
$\mathfrak {U}$
-counting systems. By Theorem 20, an ordinal
![]() $\mathfrak {U}$
-counting system has the form
$\mathfrak {U}$
-counting system has the form
![]() , where
, where
![]() $\mathcal {O}$
is an ordinal system relative to
$\mathcal {O}$
is an ordinal system relative to
![]() $\mathfrak {U}$
and
$\mathfrak {U}$
and
![]() is the join defined for exactly the successor-closed subsets
is the join defined for exactly the successor-closed subsets
![]() $I\in \mathsf {P}_{\mathfrak {U}} \mathcal {O}$
in the
$I\in \mathsf {P}_{\mathfrak {U}} \mathcal {O}$
in the
![]() $\mathfrak {U}$
-counting system.
$\mathfrak {U}$
-counting system.
For any
![]() $\mathfrak {U}$
-counting system
$\mathfrak {U}$
-counting system
![]() $(X,L,s)$
, if a morphism
$(X,L,s)$
, if a morphism
exists, it must be the unique function f defined by the transfinite recursion
-
(i)
 $f(x^+) = s(f(x))$
for any
$f(x^+) = s(f(x))$
for any
 $x\in \mathcal {O};$
$x\in \mathcal {O};$
-
(ii)
 $f(x) = L(\{f(y)\mid y<x \})$
for any limit ordinal x (Lemma 12).
$f(x) = L(\{f(y)\mid y<x \})$
for any limit ordinal x (Lemma 12).
We now prove that the function f defined by the recursion above is a morphism. It preserves succession by (i). Consider
![]() $I\in \mathsf {P}_{\mathfrak {U}} \mathcal {O}$
closed under successors. Then
$I\in \mathsf {P}_{\mathfrak {U}} \mathcal {O}$
closed under successors. Then
is a limit ordinal and
, by Theorem 20. By definition of f, we then have
We will now prove
![]() $\overline {f\overline {I}}= \overline {fI}$
. We clearly have
$\overline {f\overline {I}}= \overline {fI}$
. We clearly have
![]() $fI\subseteq \overline {f\overline {I}}$
, so it suffices to show that
$fI\subseteq \overline {f\overline {I}}$
, so it suffices to show that
![]() $f\overline {I}\subseteq \overline {fI}$
. This is equivalent to showing
$f\overline {I}\subseteq \overline {fI}$
. This is equivalent to showing
![]() $\overline {I}\subseteq f^{-1}\overline {fI}$
, which would follow if we prove
$\overline {I}\subseteq f^{-1}\overline {fI}$
, which would follow if we prove
![]() $f^{-1}\overline {fI}$
is closed. If
$f^{-1}\overline {fI}$
is closed. If
![]() $x^+\in f^{-1}\overline {fI}$
, then
$x^+\in f^{-1}\overline {fI}$
, then
![]() $s(f(x))=f(x^+)\in \overline {fI}$
. Therefore,
$s(f(x))=f(x^+)\in \overline {fI}$
. Therefore,
![]() $f(x)\in \overline {fI}$
and so
$f(x)\in \overline {fI}$
and so
![]() $x\in f^{-1}\overline {fI}$
. If
$x\in f^{-1}\overline {fI}$
. If
, then (as
is a limit ordinal by Theorem 20)
which implies
. This gives
. Note that we have the first of these two subset inclusions due to the fact that
thanks to Theorem 20. This proves that
![]() $f^{-1}\overline {fI}$
is closed. So
$f^{-1}\overline {fI}$
is closed. So
![]() $\overline {f\overline {I}}= \overline {fI}$
. We therefore get
$\overline {f\overline {I}}= \overline {fI}$
. We therefore get
, showing that f is indeed a morphism
.⊣
Consider the case when every element in
![]() $\mathfrak {U}\neq \varnothing $
is a finite set (e.g.
$\mathfrak {U}\neq \varnothing $
is a finite set (e.g.
![]() $\mathfrak {U}$
could be the universe of hereditarily finite sets). Then each triple
$\mathfrak {U}$
could be the universe of hereditarily finite sets). Then each triple
![]() $(X,0,s)$
, where X is a set, s is a function
$(X,0,s)$
, where X is a set, s is a function
![]() $s\colon X\to X$
, and
$s\colon X\to X$
, and
![]() $0\in X$
, can be seen as a
$0\in X$
, can be seen as a
![]() $\mathfrak {U}$
-counting system for the same s, with
$\mathfrak {U}$
-counting system for the same s, with
![]() $L(I{\kern-0.5pt})=0$
for each finite I. A morphism
$L(I{\kern-0.5pt})=0$
for each finite I. A morphism
![]() $f\colon (X_1,0_1,s_1)\to (X_2,0_2,s_2)$
between such
$f\colon (X_1,0_1,s_1)\to (X_2,0_2,s_2)$
between such
![]() $\mathfrak {U}$
-counting systems is a function
$\mathfrak {U}$
-counting systems is a function
![]() $f\colon X_1\to X_2$
such that
$f\colon X_1\to X_2$
such that
![]() $s_2f=fs_1$
and
$s_2f=fs_1$
and
![]() $f(0_1)=0_2$
. The natural number system
$f(0_1)=0_2$
. The natural number system
![]() $(\mathbb {N},0,s)$
, with its usual successor function
$(\mathbb {N},0,s)$
, with its usual successor function
![]() $s(n)=n+1$
, is an initial object in the category of such
$s(n)=n+1$
, is an initial object in the category of such
![]() $\mathfrak {U}$
-counting systems. Theorem 21 presents the natural number system as an initial object in the category of all
$\mathfrak {U}$
-counting systems. Theorem 21 presents the natural number system as an initial object in the category of all
![]() $\mathfrak {U}$
-counting systems. It is not surprising that the natural number system is initial in this larger category too, since the empty set is the only finite successor-closed subset of
$\mathfrak {U}$
-counting systems. It is not surprising that the natural number system is initial in this larger category too, since the empty set is the only finite successor-closed subset of
![]() $\mathbb {N}$
.
$\mathbb {N}$
.