We discuss the connection between decidability of a theory of a large algebraic extensions of 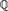${\Bbb Q}$ and the recursiveness of the field as a subset of a fixed algebraic closure. In particular, we prove that if an algebraic extension K of 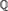${\Bbb Q}$ has a decidable existential theory, then within any fixed algebraic closure 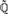$\widetilde{\Bbb Q}$ of 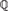${\Bbb Q}$, the field K must be conjugate over 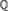${\Bbb Q}$ to a field which is recursive as a subset of the algebraic closure. We also show that for each positive integer e there are infinitely many e-tuples 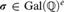$\sigma \in {\text{Gal}}\left( {\Bbb Q} \right)^e $ such that the field 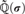$\widetilde{\Bbb Q}\left( \sigma \right)$ is primitive recursive in 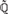$\widetilde{\Bbb Q}$ and its elementary theory is primitive recursively decidable. Moreover, 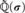$\widetilde{\Bbb Q}\left( \sigma \right)$ is PAC and 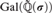${\text{Gal}}\left( {\widetilde{\Bbb Q}\left( \sigma \right)} \right)$ is isomorphic to the free profinite group on e generators.