Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-23T06:05:01.585Z Has data issue: false hasContentIssue false
  • English
  • Français

Decidability and undecidability of extensions of second (first) order theory of (generalized) successor1

Published online by Cambridge University Press:  12 March 2014

Calvin C. Elgot  and
Michael O. Rabin
Calvin C. Elgot
Affiliation:
Ibm Watson Research Center Yorktown Heights, New YorkNew York University, Hebrew University
Michael O. Rabin
Affiliation:
Ibm Watson Research Center Yorktown Heights, New YorkNew York University, Hebrew University
Get access Rights & Permissions [Opens in a new window]

Extract

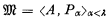We study certain first and second order theories which are semantically defined as the sets of all sentences true in certain given structures. Let be a structure where A is a non-empty set, λ is an ordinal, and Pα is an n(α)-ary relation or function4 on A. With 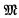we associate a language L appropriate for 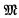which may be a first or higher order calculus. L has an n(α)-place predicate or function constant P for each α < λ. We shall study three types of languages: (1) first-order calculi with equality; (2) second-order monadic calculi which contain monadic predicate (set) variables ranging over subsets of A; (3) restricted (weak) second-order calculi which contain monadic predicate variables ranging over finite subsets of A.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 31 , Issue 2 , June 1966 , pp. 169 - 181
Copyright
Copyright © Association for Symbolic Logic 1966

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

1

Presented to the American Mathematical Society in January, 1963 under the titles “Decision Problems of Extensions of Second Order Theory of Successor” and “On the First Order Theory of Generalized Successor”.

References

REFERENCES

[1]Büchi, J. R. and Elgot, C. C., Decision problems of weak second order arithmetics and finite automata, Part I, (abstract), American Mathematical Society Notices, vol. 5 (1959), p. 834.Google Scholar
[2]Büchi, J. R., Weak second order arithmetic and finite automata, Zeitschrift für Mathematische Logik and Grundlagen der Mathematik, vol. 6 (1960), pp. 66–92.CrossRefGoogle Scholar
[3]Büchi, J. R., On a decision problem in restricted second order arithmetic, Logic Methodology and Philosophy of Sciences, Proceedings of the I960 International Congress, pp. 1–14.Google Scholar
[4]Elgot, C. C., Decision problems of finite automata design and related arithmetics, Transactions of the American Mathematical Society, vol. 98 (1961), pp. 21–51.CrossRefGoogle Scholar
[5]Quine, W. V., Concatenation as a basis of arithmetic, this Journal, vol. 11 (1946) 105–114.Google Scholar
[6]Rabin, M. O. and Scott, D., Finite automata and their decision problems, IBM Journal of Research and Development, vol. 3 (1959), pp. 114–125.CrossRefGoogle Scholar
[7]Robinson, J., General recursive functions, Proceedings of the American Mathematical Society, vol. 1 (1950), pp. 703–718.CrossRefGoogle Scholar
[8]Robinson, R. M., Restricted set — theoretical definitions in arithmetic, Proceedings of the American Mathematical Society, vol. 9 (1958), pp. 238–242.CrossRefGoogle Scholar