Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-17T20:17:20.510Z Has data issue: false hasContentIssue false
  • English
  • Français

Cupping and definability in the local structure of the enumeration degrees

Published online by Cambridge University Press:  12 March 2014

Hristo Ganchev  and
Mariya I. Soskova
Hristo Ganchev
Affiliation:
Faculty of Mathematics, Sofia University, 5 James Bourchier Bvld., 1164 Sofia, Bulgaria, E-mail: [email protected]
Mariya I. Soskova
Affiliation:
Faculty of Mathematics, Sofia University, 5 James Bourchier Bvld., 1164 Sofia, Bulgaria, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

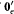We show that every splitting of in the local structure of the enumeration degrees, 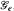, contains at least one low-cuppable member. We apply this new structural property to show that the classes of all 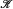-pairs in 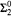, all downwards properly enumeration degrees and all upwards properly enumeration degrees are first order definable in .

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 77 , Issue 1 , March 2012 , pp. 133 - 158
Copyright
Copyright © Association for Symbolic Logic 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Arslanov, M. M., Cooper, S. B., and Kalimullin, I. Sh., Splitting properties of total enumeration degrees, Algebra and Logic, vol. 42 (2003), pp. 1–13.CrossRefGoogle Scholar
[2]Arslanov, M. M. and Sorbi, A., Relative splittings of in the ∆2 enumeration degrees, Lecture Notes in Logic, vol. 13 (1999), pp. 44–56.Google Scholar
[3]Bereznyk, S., Coles, R., and Sorbi, A., The distribution of properly e-degrees, this Journal, vol. 65 (2000), pp. 19–32.Google Scholar
[4]Cooper, S. B., Partial degrees and the density problem. Part 2: The enumeration degrees of the Σ2 sets are dense, this Journal, vol. 49 (1984), pp. 503–513.Google Scholar
[5]Cooper, S. B., Enumeration reducibilty, nondeterministic computations and relative computability of partial functions, Recursion theory week, Oberwolfach 1989 (Ambos-Spies, K., Müller, G., and Sacks, G. E., editors), Lecture Notes in Mathematics, vol. 1432, Springer-Verlag, 1990, pp. 57–110.Google Scholar
[6]Cooper, S. B., Computability theory, Chapman & Hall/CRC Mathematics, Boca Raton, FL, New York, London, 2004.Google Scholar
[7]Cooper, S. B. and Copestake, C. S., Properly Σ2 enumeration degrees, Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, vol. 34 (1988), pp. 491–522.CrossRefGoogle Scholar
[8]Cooper, S. B., Li, A., Sorbi, A., and Yang, Y., Bounding and nonbounding minimal pairs in the enumeration degrees, this Journal, vol. 70 (2005), pp. 741–766.Google Scholar
[9]Cooper, S. B., Sorbi, A., and Yi, X., Cupping and noncupping in the enumeration degrees of sets, Annals of Pure and Applied Logic, vol. 82 (1996), pp. 317–342.CrossRefGoogle Scholar
[10]Copestake, C., 1-Genericity in the enumeration degrees, this Journal, vol. 53 (1988), pp. 878–887.Google Scholar
[11]Friedberg, R. M. and Rogers, H. Jr., Reducibility and completeness for sets of integers, Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, vol. 5 (1959), pp. 117–125.CrossRefGoogle Scholar
[12]Ganchev, H. and Soskova, M. I., Embedding distributive lattices in the enumeration degrees, Journal of Logic and Computation, accepted.Google Scholar
[13]Ganchev, H. and Soskova, M. I., The high/low hierarchy in the local structure of the ω-enumeration degrees, Annals of Pure and Applied Logic, accepted.Google Scholar
[14]Ganchev, H. and Soskova, M. I., Interpreting true arithmetic in the local structure of the enumeration degrees, in preparation.Google Scholar
[15]Jockusch, C. G., Semirecursive sets and positive reducibility, Transactions of the American Mathematical Society, vol. 131 (1968), pp. 420–436.CrossRefGoogle Scholar
[16]Kalimullin, I. Sh., Definability of the jump operator in the enumeration degrees, Journal of Mathematical Logic, vol. 3 (2003), pp. 257–267.CrossRefGoogle Scholar
[17]Lachlan, A. H. and Shore, R. A., The n-rea enumeration degrees are dense, Archive for Mathematical Logic, vol. 31 (1992), pp. 277–285.CrossRefGoogle Scholar
[18]McEvoy, K., Jumps of quasi-minimal enumeration degrees, this Journal, vol. 50 (1985), pp. 839–848.Google Scholar
[19]Sorbi, A., The enumeration degrees of the sets, Complexity, logic and recursion theory (Sorbi, A., editor), Marcel Dekker, 1997, pp. 303–330.Google Scholar
[20]Soskova, M. I., A non-splitting theorem in the enumeration degrees, Annals of Pure and Applied Logic, vol. 160 (2009), pp. 400–418.CrossRefGoogle Scholar
[21]Soskova, M.I. and Wu, G., Cupping enumeration degrees, Mathematical Structures in Computer Science, vol. 19 (2009), pp. 169–191.CrossRefGoogle Scholar