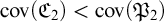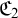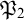1 Introduction
Given any set X with at least two elements,
![]() $b\in [\omega ]^\omega $
and
$b\in [\omega ]^\omega $
and
![]() $A\subseteq \,^\omega X$
, let
$A\subseteq \,^\omega X$
, let
![]() $\Gamma _X(A,b)$
be the infinite game of two players in which both players choose the consecutive elements of a sequence
$\Gamma _X(A,b)$
be the infinite game of two players in which both players choose the consecutive elements of a sequence
![]() $x\in \, ^\omega X$
. The choice of
$x\in \, ^\omega X$
. The choice of
![]() $x(n)$
is done by the second player iff
$x(n)$
is done by the second player iff
![]() $n\in b$
. The first player wins iff
$n\in b$
. The first player wins iff
![]() $x\in A$
. By using such games, Mycielski [Reference Mycielski7] introduced ideals on the space
$x\in A$
. By using such games, Mycielski [Reference Mycielski7] introduced ideals on the space
![]() $^\omega X$
as follows: Given a family
$^\omega X$
as follows: Given a family
![]() $\mathfrak {B} =\langle b_s :s\in \,^{<\omega }2\rangle $
of infinite subsets of
$\mathfrak {B} =\langle b_s :s\in \,^{<\omega }2\rangle $
of infinite subsets of
![]() $\omega $
such that
$\omega $
such that
![]() $b_s=b_{s^{\,\smallfrown \,} 0}\,\dot \cup \,b_{s^{\,\smallfrown \,}1}$
(disjoint union), the Mycielski ideal
$b_s=b_{s^{\,\smallfrown \,} 0}\,\dot \cup \,b_{s^{\,\smallfrown \,}1}$
(disjoint union), the Mycielski ideal
![]() $\mathfrak {M}_{X,\mathfrak {B}}$
is defined as the collection of all
$\mathfrak {M}_{X,\mathfrak {B}}$
is defined as the collection of all
![]() $A\subseteq \,^\omega X$
such that for all
$A\subseteq \,^\omega X$
such that for all
![]() $s\in \,^{<\omega }2$
the second player has a winning strategy in the game
$s\in \,^{<\omega }2$
the second player has a winning strategy in the game
![]() $\Gamma _{X,b_s}$
. In [Reference Mycielski7], Mycielski proved, among other things, that if
$\Gamma _{X,b_s}$
. In [Reference Mycielski7], Mycielski proved, among other things, that if
![]() $X=2$
or
$X=2$
or
![]() $X=\omega $
, then
$X=\omega $
, then
![]() $\mathfrak {M}_{X,\mathfrak {B}}$
is a translation invariant
$\mathfrak {M}_{X,\mathfrak {B}}$
is a translation invariant
![]() $\sigma $
-ideal that is orthogonal to
$\sigma $
-ideal that is orthogonal to
![]() $\mathcal {M}\cap \mathcal {N}$
, where
$\mathcal {M}\cap \mathcal {N}$
, where
![]() $\mathcal {M}$
and
$\mathcal {M}$
and
![]() $\mathcal {N}$
are the ideals of meager and null sets, respectively (see [Reference Rosłanowski8, Theorem 2.2] for a list of Mycielski’s results). Rosłanowski [Reference Rosłanowski8] introduced more ideals, denoted
$\mathcal {N}$
are the ideals of meager and null sets, respectively (see [Reference Rosłanowski8, Theorem 2.2] for a list of Mycielski’s results). Rosłanowski [Reference Rosłanowski8] introduced more ideals, denoted
![]() $\mathfrak {C}_X$
and
$\mathfrak {C}_X$
and
![]() $\mathfrak {P}_X$
, that are closely related to Mycielski’s
$\mathfrak {P}_X$
, that are closely related to Mycielski’s
![]() $\mathfrak {M}_{X,\mathfrak {B}}$
and are also called Mycielski ideals.
$\mathfrak {M}_{X,\mathfrak {B}}$
and are also called Mycielski ideals.
Definition 1.1. Let X be a set with at least two elements. Let
![]() $\mathfrak {C}_X$
be the set of all
$\mathfrak {C}_X$
be the set of all
![]() $A\subseteq \,^\omega X$
for which player II has a winning strategy in the game
$A\subseteq \,^\omega X$
for which player II has a winning strategy in the game
![]() $\Gamma _X(A,b)$
for every
$\Gamma _X(A,b)$
for every
![]() $b\in [\omega ]^\omega $
, thus
$b\in [\omega ]^\omega $
, thus
Moreover, let
Here
![]() $A\upharpoonright b=\lbrace x\upharpoonright b: x\in A\rbrace $
. Alternatively,
$A\upharpoonright b=\lbrace x\upharpoonright b: x\in A\rbrace $
. Alternatively,
![]() $\mathfrak {P}_X$
is the set of those
$\mathfrak {P}_X$
is the set of those
![]() $A\subseteq \, ^\omega X$
for which, for every
$A\subseteq \, ^\omega X$
for which, for every
![]() $b\in [\omega ]^\omega $
, player II has a winning strategy in the game
$b\in [\omega ]^\omega $
, player II has a winning strategy in the game
![]() $\Gamma _X(A,b)$
that does not depend on the moves of player I. Clearly we have
$\Gamma _X(A,b)$
that does not depend on the moves of player I. Clearly we have
![]() $\mathfrak {P}_X\subseteq \mathfrak {C}_X$
.
$\mathfrak {P}_X\subseteq \mathfrak {C}_X$
.
The Mycielski ideals
![]() $\mathfrak {C}_X$
and
$\mathfrak {C}_X$
and
![]() $\mathfrak {P}_X$
have been the object of intensive research over the past decades. The main focus has been on their cardinal characteristics. Recall the following cardinals associated with any ideal
$\mathfrak {P}_X$
have been the object of intensive research over the past decades. The main focus has been on their cardinal characteristics. Recall the following cardinals associated with any ideal
![]() $\mathfrak {I}$
on a set Y:
$\mathfrak {I}$
on a set Y:
 $$ \begin{align*} &\mathrm{add}(\mathfrak{I})\;=\;\min\{ |\mathcal{F}|: \mathcal{F}\subseteq \mathfrak{I}\;\wedge\; \bigcup\mathcal{F}\not\in \mathfrak{I}\}, \notag \\ &\mathrm{cov}(\mathfrak{I})\;=\;\min\{ |\mathcal{F}|: \mathcal{F}\subseteq \mathfrak{I}\;\wedge\; \bigcup\mathcal{F}= Y\}, \notag \\ &\mathrm{non}(\mathfrak{I})\;=\;\min\{ |Z|: Z\subseteq Y\;\wedge\;Z\not\in \mathfrak{I}\},\phantom{\bigcup} \notag \\ &\mathrm{cof}(\mathfrak{I})\;=\;\min\{ |\mathcal{F}|: \mathcal{F}\subseteq \mathfrak{I} \;\wedge\; \forall Z\in \mathfrak{I} \;\: \exists Z'\in \mathcal{F}\;\:Z\subseteq Z'\}. \phantom{\bigcup} \notag \end{align*} $$
$$ \begin{align*} &\mathrm{add}(\mathfrak{I})\;=\;\min\{ |\mathcal{F}|: \mathcal{F}\subseteq \mathfrak{I}\;\wedge\; \bigcup\mathcal{F}\not\in \mathfrak{I}\}, \notag \\ &\mathrm{cov}(\mathfrak{I})\;=\;\min\{ |\mathcal{F}|: \mathcal{F}\subseteq \mathfrak{I}\;\wedge\; \bigcup\mathcal{F}= Y\}, \notag \\ &\mathrm{non}(\mathfrak{I})\;=\;\min\{ |Z|: Z\subseteq Y\;\wedge\;Z\not\in \mathfrak{I}\},\phantom{\bigcup} \notag \\ &\mathrm{cof}(\mathfrak{I})\;=\;\min\{ |\mathcal{F}|: \mathcal{F}\subseteq \mathfrak{I} \;\wedge\; \forall Z\in \mathfrak{I} \;\: \exists Z'\in \mathcal{F}\;\:Z\subseteq Z'\}. \phantom{\bigcup} \notag \end{align*} $$
Trivially, if
![]() $\mathfrak {I}, \mathfrak {J}$
are ideals such that
$\mathfrak {I}, \mathfrak {J}$
are ideals such that
![]() $\mathfrak {I}\subseteq \mathfrak {J}$
, then cov
$\mathfrak {I}\subseteq \mathfrak {J}$
, then cov
![]() $(\mathfrak {J})\leq \,\mathrm {cov}(\mathfrak {I})$
.
$(\mathfrak {J})\leq \,\mathrm {cov}(\mathfrak {I})$
.
There exists a close relation between
![]() $\mathfrak {P}_k$
and
$\mathfrak {P}_k$
and
![]() $\mathfrak {C}_k$
, where
$\mathfrak {C}_k$
, where
![]() $2\leq k<\omega $
, on the one hand, and the tree ideals
$2\leq k<\omega $
, on the one hand, and the tree ideals
![]() $v^0_k$
,
$v^0_k$
,
![]() $u^0_k$
associated with k-dimensional Silver forcing
$u^0_k$
associated with k-dimensional Silver forcing
![]() $\mathbb {SI}_k$
and forcing with k-dimensional uniform Sacks trees
$\mathbb {SI}_k$
and forcing with k-dimensional uniform Sacks trees
![]() $\mathbb {U}_k$
, respectively, on the other hand. See Definition 2.1 below for their definitions. This relation comes from the fact that a winning strategy for player II in the game
$\mathbb {U}_k$
, respectively, on the other hand. See Definition 2.1 below for their definitions. This relation comes from the fact that a winning strategy for player II in the game
![]() $\Gamma _k(A,b)$
, where b is infinite and coinfinite, can be considered as a perfect tree
$\Gamma _k(A,b)$
, where b is infinite and coinfinite, can be considered as a perfect tree
![]() $u^b \subseteq \,^{<\omega }k$
with the property that for every
$u^b \subseteq \,^{<\omega }k$
with the property that for every
![]() $t\in u^b$
, t is a splitnode of
$t\in u^b$
, t is a splitnode of
![]() $u^b$
iff
$u^b$
iff
![]() $\vert t\vert \in \omega \setminus b$
and every splitnode splits into k successor nodes. Such trees are the k-dimensional uniform Sacks trees. If
$\vert t\vert \in \omega \setminus b$
and every splitnode splits into k successor nodes. Such trees are the k-dimensional uniform Sacks trees. If
![]() $u^b$
does not depend on the moves of player II, then
$u^b$
does not depend on the moves of player II, then
![]() $u^b$
is nothing else than a k-dimensional Silver function with domain b.
$u^b$
is nothing else than a k-dimensional Silver function with domain b.
The inclusions
![]() $\mathfrak {P}_k\subseteq v^0_k$
and
$\mathfrak {P}_k\subseteq v^0_k$
and
![]() $\mathfrak {C}_k\subseteq u^0_k$
are pretty obvious (see [Reference Kuiper and Spinas5, Lemma 4.1]); however, no equality is provable here. Moreover, no inclusion between
$\mathfrak {C}_k\subseteq u^0_k$
are pretty obvious (see [Reference Kuiper and Spinas5, Lemma 4.1]); however, no equality is provable here. Moreover, no inclusion between
![]() $v^0_k$
and
$v^0_k$
and
![]() $u^0_k$
is provable (see [Reference Kuiper and Spinas5, Section 4] for these results). By general knowledge, if
$u^0_k$
is provable (see [Reference Kuiper and Spinas5, Section 4] for these results). By general knowledge, if
![]() $j^0$
is the tree ideal associated with some proper tree forcing P, then in the model obtained by a countable support iteration of length
$j^0$
is the tree ideal associated with some proper tree forcing P, then in the model obtained by a countable support iteration of length
![]() $\omega _2$
of P over a model of CH, which will be called the P-model for short below, cov
$\omega _2$
of P over a model of CH, which will be called the P-model for short below, cov
![]() $(j^0) =\aleph _2$
holds true. E.g., see [Reference Judah, Miller and Shelah4, Theorem 1.2] where this is proved for the two-dimensional Sacks forcing.
$(j^0) =\aleph _2$
holds true. E.g., see [Reference Judah, Miller and Shelah4, Theorem 1.2] where this is proved for the two-dimensional Sacks forcing.
We conclude from the above that in the
![]() $\mathbb {SI}_k$
-model cov(
$\mathbb {SI}_k$
-model cov(
![]() $\mathfrak {P}_k) =\aleph _2$
holds and in the
$\mathfrak {P}_k) =\aleph _2$
holds and in the
![]() $\mathbb {U}_k$
-model cov(
$\mathbb {U}_k$
-model cov(
![]() $\mathfrak {C}_k )=\,\mathrm {cov}(\mathfrak {P}_k )=\aleph _2$
. A main result of [Reference Shelah and Steprāns10] is that the equality cov
$\mathfrak {C}_k )=\,\mathrm {cov}(\mathfrak {P}_k )=\aleph _2$
. A main result of [Reference Shelah and Steprāns10] is that the equality cov
![]() $(\mathfrak {P}_k)=\,\mathrm {cov}(\mathfrak {P}_{k+1})$
holds in ZFC, for every
$(\mathfrak {P}_k)=\,\mathrm {cov}(\mathfrak {P}_{k+1})$
holds in ZFC, for every
![]() $2\leq k<\omega $
. In [Reference Kuiper and Spinas5, Theorem 7.18] it has been shown that in the
$2\leq k<\omega $
. In [Reference Kuiper and Spinas5, Theorem 7.18] it has been shown that in the
![]() $\mathbb {U}_k$
-model cov
$\mathbb {U}_k$
-model cov
![]() $( \mathfrak {C}_{k+1})=\aleph _1$
. By the results just mentioned and as by [Reference Kuiper and Spinas5, Proposition 6.8] cov
$( \mathfrak {C}_{k+1})=\aleph _1$
. By the results just mentioned and as by [Reference Kuiper and Spinas5, Proposition 6.8] cov
![]() $(\mathfrak {C}_{k+1})\leq \, \mathrm {cov}(\mathfrak {C}_{k} )$
is always true, we conclude that in the
$(\mathfrak {C}_{k+1})\leq \, \mathrm {cov}(\mathfrak {C}_{k} )$
is always true, we conclude that in the
![]() $\mathbb {U}_2$
-model we have cov
$\mathbb {U}_2$
-model we have cov
![]() $ (\mathfrak {C}_{k}) <\,\mathrm {cov}(\mathfrak {P}_{k})$
for every
$ (\mathfrak {C}_{k}) <\,\mathrm {cov}(\mathfrak {P}_{k})$
for every
![]() $3\leq k<\omega $
, but cov
$3\leq k<\omega $
, but cov
![]() $(\mathfrak {C}_{2})=\,\mathrm {cov}(\mathfrak {P}_{2})=\aleph _2$
. Hence the consistency of cov
$(\mathfrak {C}_{2})=\,\mathrm {cov}(\mathfrak {P}_{2})=\aleph _2$
. Hence the consistency of cov
![]() $(\mathfrak {C}_{2})<\,\mathrm {cov}(\mathfrak {P}_{2})$
was left open.
$(\mathfrak {C}_{2})<\,\mathrm {cov}(\mathfrak {P}_{2})$
was left open.
Our main result here is that cov
![]() $(\mathfrak {C}_{2})<\,\mathrm {cov}(\mathfrak {P}_{2})$
is true in the
$(\mathfrak {C}_{2})<\,\mathrm {cov}(\mathfrak {P}_{2})$
is true in the
![]() $\mathbb {SI}_2$
-model. For this we have to define
$\mathbb {SI}_2$
-model. For this we have to define
![]() $\aleph _1$
-many
$\aleph _1$
-many
![]() $\mathfrak {C}_{2}$
-sets that cover
$\mathfrak {C}_{2}$
-sets that cover
![]() $^\omega 2$
in the Silver model. A
$^\omega 2$
in the Silver model. A
![]() $\mathfrak {C}_{2}$
-set can be coded by a family
$\mathfrak {C}_{2}$
-set can be coded by a family
![]() $C=\langle u^b: b\in \Omega \rangle $
, where
$C=\langle u^b: b\in \Omega \rangle $
, where
![]() $\Omega \subseteq [\omega ]^\omega $
is
$\Omega \subseteq [\omega ]^\omega $
is
![]() $\subseteq $
-dense and every
$\subseteq $
-dense and every
![]() $u^b$
is a strategy for player II in the game
$u^b$
is a strategy for player II in the game
![]() $\Gamma _2(\cdot , b)$
, thus a uniform Sacks tree with
$\Gamma _2(\cdot , b)$
, thus a uniform Sacks tree with
![]() $\omega \setminus b$
as its set of split-levels, as described above. Such C will be called coding system below. Then
$\omega \setminus b$
as its set of split-levels, as described above. Such C will be called coding system below. Then
is the
![]() $\mathfrak {C}_{2}$
-set coded by C. Clearly, sets of this type form a base of
$\mathfrak {C}_{2}$
-set coded by C. Clearly, sets of this type form a base of
![]() $\mathfrak {C}_{2}$
. Clearly, no dense
$\mathfrak {C}_{2}$
. Clearly, no dense
![]() $\Omega $
in the ground model will remain so in a forcing extension adding reals. Indeed, given any new real x, say
$\Omega $
in the ground model will remain so in a forcing extension adding reals. Indeed, given any new real x, say
![]() $x\in \, ^\omega 2$
, the set
$x\in \, ^\omega 2$
, the set
![]() $\lbrace x\upharpoonright n: n<\omega \rbrace \subset \, ^{<\omega } 2$
does not contain any infinite subset from the ground model. Therefore, one of our tasks will be to extend
$\lbrace x\upharpoonright n: n<\omega \rbrace \subset \, ^{<\omega } 2$
does not contain any infinite subset from the ground model. Therefore, one of our tasks will be to extend
![]() $\aleph _1$
-many partial coding systems cofinally often during the forcing iteration.
$\aleph _1$
-many partial coding systems cofinally often during the forcing iteration.
There are two main ingredients for this construction to work. The first one consists in a careful reading of a given
![]() $P_{\omega _2}$
-name
$P_{\omega _2}$
-name
![]() $\dot x$
for a new real, where
$\dot x$
for a new real, where
![]() $P_{\omega _2}$
is the CS-iteration of
$P_{\omega _2}$
is the CS-iteration of
![]() $\mathbb {SI}_2$
. This process will produce (even for a name for a member of
$\mathbb {SI}_2$
. This process will produce (even for a name for a member of
![]() $^\omega \omega $
) a fusion sequence
$^\omega \omega $
) a fusion sequence
![]() $\bar S=\langle p_n:n<\omega \rangle $
with limit
$\bar S=\langle p_n:n<\omega \rangle $
with limit
![]() $p_\omega $
in
$p_\omega $
in
![]() $P_{\omega _2}$
together with a 2-splitting tree T, i.e., every node of T has at most two successor nodes, which is the tree of possibilities for
$P_{\omega _2}$
together with a 2-splitting tree T, i.e., every node of T has at most two successor nodes, which is the tree of possibilities for
![]() $\dot x$
below
$\dot x$
below
![]() $p_\omega $
, such that the family of refining finite maximal antichains below
$p_\omega $
, such that the family of refining finite maximal antichains below
![]() $p_\omega $
associated with
$p_\omega $
associated with
![]() $\bar S$
corresponds to the split-levels of T. For this we apply what we call the Grigorieff dichotomy, i.e., an idea that appears in seminal form in Grigorieff’s paper [Reference Grigorieff3] where it is shown that
$\bar S$
corresponds to the split-levels of T. For this we apply what we call the Grigorieff dichotomy, i.e., an idea that appears in seminal form in Grigorieff’s paper [Reference Grigorieff3] where it is shown that
![]() $\mathbb {SI}_2$
(as well as many more forcings of a similar type) adds a minimal real.
$\mathbb {SI}_2$
(as well as many more forcings of a similar type) adds a minimal real.
As a small digression let me mention that in [Reference Rosłanowski and Steprāns9] the property of some forcing that in its extension every new real is a branch through some k-ary tree in the ground model is called k-localization property. In [Reference Rosłanowski and Steprāns9] it is shown that the CS-iteration of
![]() $\mathbb {SI}_k$
has the k-localization property. For this, Shelah-style preservation theorems are used and it is said that“maybe some old wisdom got lost”, but that it seemed impossible to prove this by classical methods. I think that this old wisdom are Grigorieff’s ideas, as building on them the
$\mathbb {SI}_k$
has the k-localization property. For this, Shelah-style preservation theorems are used and it is said that“maybe some old wisdom got lost”, but that it seemed impossible to prove this by classical methods. I think that this old wisdom are Grigorieff’s ideas, as building on them the
![]() $2$
-localization property for
$2$
-localization property for
![]() $P_{\omega _2}$
can be shown by using a classical fusion construction. I conjecture that this can be generalized to every finite dimension. But then certainly some extra complexity is added, as
$P_{\omega _2}$
can be shown by using a classical fusion construction. I conjecture that this can be generalized to every finite dimension. But then certainly some extra complexity is added, as
![]() $\mathbb {SI}_k$
is no longer minimal if
$\mathbb {SI}_k$
is no longer minimal if
![]() $k\geq 3$
.Footnote
1
$k\geq 3$
.Footnote
1
The second ingredient for our main result is a new idea by which it is possible to define, for any
![]() $P_{\omega _2} $
-name
$P_{\omega _2} $
-name
![]() $\dot x$
for a real with fusion
$\dot x$
for a real with fusion
![]() $\bar S$
and limit
$\bar S$
and limit
![]() $p_\omega $
as above, a coding system
$p_\omega $
as above, a coding system
![]() $C=\langle u^b:b\in \Omega \rangle $
in the ground model such that
$C=\langle u^b:b\in \Omega \rangle $
in the ground model such that
Moreover, the definition of C depends only on the isomorphism type of
![]() $\dot x$
(see Definition 4.2 below). As by CH in the ground model there are only
$\dot x$
(see Definition 4.2 below). As by CH in the ground model there are only
![]() $\aleph _1$
-many such types, this will be a good start for the construction of the
$\aleph _1$
-many such types, this will be a good start for the construction of the
![]() $\aleph _1 \mathfrak {C}_2$
-sets we need to have in the final model. This new idea is inspired by the well-known proof that
$\aleph _1 \mathfrak {C}_2$
-sets we need to have in the final model. This new idea is inspired by the well-known proof that
![]() $\mathbb {SI}_2$
adds a real which splits every infinite subset of
$\mathbb {SI}_2$
adds a real which splits every infinite subset of
![]() $\omega $
in the ground model.
$\omega $
in the ground model.
In [Reference Kuiper and Spinas6], the ideas of this work have been used to show that in the model obtained by a CS-iteration of Sacks forcing the inequality
![]() $\mathrm {cov}(\mathfrak {C}_2)<\mathrm {cov}(s^0)$
holds true. The value of
$\mathrm {cov}(\mathfrak {C}_2)<\mathrm {cov}(s^0)$
holds true. The value of
![]() $\mathrm {cov}(\mathfrak {P}_2)$
in the Sacks model is not known.
$\mathrm {cov}(\mathfrak {P}_2)$
in the Sacks model is not known.
2 Basic definitions
Definition 2.1. Let
![]() $2\leq k<\omega $
.
$2\leq k<\omega $
.
(1) Let
![]() $\mathbb {SI}_k$
denote k-dimensional Silver forcing, i.e., the set of all partial functions f from
$\mathbb {SI}_k$
denote k-dimensional Silver forcing, i.e., the set of all partial functions f from
![]() $\omega $
to k such that
$\omega $
to k such that
![]() $\omega \setminus \,\mathrm {dom}(f)$
is infinite, ordered by extension. We shall denote
$\omega \setminus \,\mathrm {dom}(f)$
is infinite, ordered by extension. We shall denote
![]() $\omega \setminus \,\mathrm {dom}(f)$
by
$\omega \setminus \,\mathrm {dom}(f)$
by
![]() $\mathrm {com}(f)$
. So Silver forcing
$\mathrm {com}(f)$
. So Silver forcing
![]() $\mathbb {SI}$
is
$\mathbb {SI}$
is
![]() $\mathbb {SI}_2$
. By
$\mathbb {SI}_2$
. By
![]() $e_f$
we shall denote the increasing enumeration of
$e_f$
we shall denote the increasing enumeration of
![]() $\mathrm {com}(f)$
.
$\mathrm {com}(f)$
.
Given such k-dimensional Silver function f and
![]() $s\in \, ^{<\omega }k$
, by
$s\in \, ^{<\omega }k$
, by
![]() $f^s$
we denote the Silver function extending f such that we have
$f^s$
we denote the Silver function extending f such that we have
![]() $\mathrm {dom}(f^s)=\,\mathrm {dom}(f)\cup \lbrace e_f(i):i<\vert s\vert \rbrace $
and
$\mathrm {dom}(f^s)=\,\mathrm {dom}(f)\cup \lbrace e_f(i):i<\vert s\vert \rbrace $
and
![]() $f^s(e_f(i))=s(i)$
for every
$f^s(e_f(i))=s(i)$
for every
![]() $i<\vert s\vert $
.
$i<\vert s\vert $
.
Given
![]() $f,f'\in \mathbb {SI}_k$
and
$f,f'\in \mathbb {SI}_k$
and
![]() $n<\omega $
, we define
$n<\omega $
, we define
![]() $f'\leq ^n f$
iff
$f'\leq ^n f$
iff
![]() $f'\leq f$
and
$f'\leq f$
and
![]() $\mathrm {com}(f)$
and
$\mathrm {com}(f)$
and
![]() $\mathrm {com}(f')$
agree on their first
$\mathrm {com}(f')$
agree on their first
![]() $n+1$
elements. It is well-known that, equipped with these orderings,
$n+1$
elements. It is well-known that, equipped with these orderings,
![]() $\mathbb {SI}_k$
satisfies Axiom A (see [Reference Baumgartner and Mathias1] for this notion).
$\mathbb {SI}_k$
satisfies Axiom A (see [Reference Baumgartner and Mathias1] for this notion).
Given
![]() $f\in \mathbb {SI}_k$
, by
$f\in \mathbb {SI}_k$
, by
![]() $[f]$
we denote its body, which is defined as
$[f]$
we denote its body, which is defined as
The k-dimensional Silver ideal
![]() $v^0_k$
is defined as the set of all
$v^0_k$
is defined as the set of all
![]() $X\subseteq \, ^{\omega }k$
such that
$X\subseteq \, ^{\omega }k$
such that
(2) By
![]() $\mathbb {U}_k$
we denote k-dimensional uniform (Sacks) tree forcing, i.e., the set of all perfect trees
$\mathbb {U}_k$
we denote k-dimensional uniform (Sacks) tree forcing, i.e., the set of all perfect trees
![]() $u\subseteq \, ^{<\omega }k$
such that there exists an infinite and coinfinite set
$u\subseteq \, ^{<\omega }k$
such that there exists an infinite and coinfinite set
![]() $a^{u}\subset \omega $
with the property that for every node
$a^{u}\subset \omega $
with the property that for every node
![]() $t\in u$
, t is a splitnode of u iff
$t\in u$
, t is a splitnode of u iff
![]() $\vert t\vert \in a^{u}$
and every splitnode of u has full splitting, i.e., it has k immediate successors. The order on
$\vert t\vert \in a^{u}$
and every splitnode of u has full splitting, i.e., it has k immediate successors. The order on
![]() $\mathbb {U}_k$
is inclusion. We shall denote
$\mathbb {U}_k$
is inclusion. We shall denote
![]() $\mathbb {U}_2$
by
$\mathbb {U}_2$
by
![]() $\mathbb {U}$
.
$\mathbb {U}$
.
If
![]() $u\in \mathbb {U}_k $
, by
$u\in \mathbb {U}_k $
, by
![]() $[u]$
we denote the body of u, i.e., the set of all its branches. The tree ideal associated with
$[u]$
we denote the body of u, i.e., the set of all its branches. The tree ideal associated with
![]() $\mathbb {U}_k$
, denoted by
$\mathbb {U}_k$
, denoted by
![]() $u^0_k$
, is defined analogously as
$u^0_k$
, is defined analogously as
![]() $v^0_k$
: It contains all
$v^0_k$
: It contains all
![]() $X\subseteq \,^\omega k$
such that for every
$X\subseteq \,^\omega k$
such that for every
![]() $u\in \mathbb {U}_k$
there is
$u\in \mathbb {U}_k$
there is
![]() $u'\in \mathbb {U}_k$
with
$u'\in \mathbb {U}_k$
with
![]() $u'\leq u$
and
$u'\leq u$
and
![]() $[u']\cap X=\emptyset $
.
$[u']\cap X=\emptyset $
.
(3) Given any tree T, by
![]() $\mathrm {split}(T)$
we denote the set of all splitnodes of T, i.e., those
$\mathrm {split}(T)$
we denote the set of all splitnodes of T, i.e., those
![]() $t\in T$
which have at least two immediate successors. By
$t\in T$
which have at least two immediate successors. By
![]() $\mathrm {split}_n(T)$
we denote the nth splitlevel of T, i.e., the set of those
$\mathrm {split}_n(T)$
we denote the nth splitlevel of T, i.e., the set of those
![]() $t\in \,\mathrm {split}(T)$
which have precisely n proper initial segments which are splitnodes of T.
$t\in \,\mathrm {split}(T)$
which have precisely n proper initial segments which are splitnodes of T.
Definition 2.2. Let
![]() $P_\alpha $
be the CS-iteration of
$P_\alpha $
be the CS-iteration of
![]() $\mathbb {S I} $
of length
$\mathbb {S I} $
of length
![]() $\alpha $
, in particular, its elements are functions p with countable
$\alpha $
, in particular, its elements are functions p with countable
![]() $\mathrm {supp}(p):=\mathrm {dom}(p)\subseteq \alpha $
such that for every
$\mathrm {supp}(p):=\mathrm {dom}(p)\subseteq \alpha $
such that for every
![]() $\beta \in \mathrm {supp}(p)$
we have that
$\beta \in \mathrm {supp}(p)$
we have that
![]() $p(\beta )$
is a
$p(\beta )$
is a
![]() $P_\beta $
-name and the maximal condition in
$P_\beta $
-name and the maximal condition in
![]() $P_\beta $
forces
$P_\beta $
forces
![]() $ p(\beta )\in \mathbb {SI} ^{\mathbf {V}^{P_\beta }}.$
$ p(\beta )\in \mathbb {SI} ^{\mathbf {V}^{P_\beta }}.$
As explained in detail in [Reference Baumgartner and Mathias1, Section 5], given
![]() $\beta <\alpha $
,
$\beta <\alpha $
,
![]() $P_\alpha $
is forcing equivalent to an iteration
$P_\alpha $
is forcing equivalent to an iteration
![]() $P_\beta \ast P_\alpha /\dot {G}_\beta $
, where
$P_\beta \ast P_\alpha /\dot {G}_\beta $
, where
![]() $\dot {G}_\beta $
is the canonical
$\dot {G}_\beta $
is the canonical
![]() $P_\beta $
-name for the
$P_\beta $
-name for the
![]() $P_\beta $
-generic filter, such that
$P_\beta $
-generic filter, such that
![]() $P_\alpha /\dot {G}_\beta $
is again (the
$P_\alpha /\dot {G}_\beta $
is again (the
![]() $P_\beta $
-name of) a CS-support iteration of
$P_\beta $
-name of) a CS-support iteration of
![]() $\mathbb {SI}$
. Using this identification, given
$\mathbb {SI}$
. Using this identification, given
![]() $p\in P_\alpha $
and a
$p\in P_\alpha $
and a
![]() $P_\beta $
-generic filter
$P_\beta $
-generic filter
![]() $G_\beta $
, we can partially evaluate
$G_\beta $
, we can partially evaluate
![]() $p[ G_\beta ] $
as a pair of sequences
$p[ G_\beta ] $
as a pair of sequences
![]() $(\underline {f},\overline {f})$
such that
$(\underline {f},\overline {f})$
such that
![]() $\underline {f}=\langle f_\gamma :\gamma \in \mathrm {supp}(p)\cap \beta \rangle $
is a sequence of Silver functions
$\underline {f}=\langle f_\gamma :\gamma \in \mathrm {supp}(p)\cap \beta \rangle $
is a sequence of Silver functions
![]() $f_\gamma =p(\gamma )[G_\beta ]$
and
$f_\gamma =p(\gamma )[G_\beta ]$
and
![]() $\overline {f}=\langle \dot {f}_\gamma : \gamma \in \mathrm {supp}(p)\setminus \beta \rangle $
is a condition of the CS-iteration of
$\overline {f}=\langle \dot {f}_\gamma : \gamma \in \mathrm {supp}(p)\setminus \beta \rangle $
is a condition of the CS-iteration of
![]() $\mathbb {SI}$
along
$\mathbb {SI}$
along
![]() $\alpha \setminus \beta $
in
$\alpha \setminus \beta $
in
![]() $\mathbf {V}[G_\beta ]$
.
$\mathbf {V}[G_\beta ]$
.
As is well-known from proper forcing, we may assume that all
![]() $p\in P_\alpha $
are hereditarily countable (see [Reference Shelah11, Chapter III, Definition 4.1] for this notion and proof of this fact), hence in particular, for every
$p\in P_\alpha $
are hereditarily countable (see [Reference Shelah11, Chapter III, Definition 4.1] for this notion and proof of this fact), hence in particular, for every
![]() $\beta \in \,\mathrm {supp}(p) $
, the
$\beta \in \,\mathrm {supp}(p) $
, the
![]() $P_\beta $
-name
$P_\beta $
-name
![]() $p(\beta )$
can be evaluated as a Silver function by
$p(\beta )$
can be evaluated as a Silver function by
![]() $\langle g_\gamma : \gamma \in \, \mathrm {supp}(p)\cap \beta \rangle $
, where
$\langle g_\gamma : \gamma \in \, \mathrm {supp}(p)\cap \beta \rangle $
, where
![]() $g_\gamma $
is the Silver real added by the
$g_\gamma $
is the Silver real added by the
![]() $\gamma $
th iterand.
$\gamma $
th iterand.
Wlog we may assume
![]() $0,1\in \,\mathrm {supp}(p) $
for every p.
$0,1\in \,\mathrm {supp}(p) $
for every p.
(1) For
![]() $p,q\in P_\alpha $
,
$p,q\in P_\alpha $
,
![]() $F\in \left [ \mathrm {{supp}}(p)\right ] ^{<\aleph _0}$
and
$F\in \left [ \mathrm {{supp}}(p)\right ] ^{<\aleph _0}$
and
![]() $\eta : F\rightarrow \omega $
we call the triple
$\eta : F\rightarrow \omega $
we call the triple
![]() $(p,F,\eta )$
a fusion condition and we write
$(p,F,\eta )$
a fusion condition and we write
![]() $q\leq _{F,\eta }p$
for
$q\leq _{F,\eta }p$
for
(2) A fusion sequence in
![]() $P_\alpha $
is a sequence
$P_\alpha $
is a sequence
![]() $\bar S=\langle (p_n,F_n,\eta _n): n<\omega \rangle $
of fusion conditions such that
$\bar S=\langle (p_n,F_n,\eta _n): n<\omega \rangle $
of fusion conditions such that
-
(a)
 $F_0=F_1=\left \lbrace 0\right \rbrace $
,
$F_0=F_1=\left \lbrace 0\right \rbrace $
,
 $F_2=\lbrace 0,1\rbrace $
(as long as
$F_2=\lbrace 0,1\rbrace $
(as long as
 $\alpha>1$
of course),
$\alpha>1$
of course),
 $F_n\subseteq F_{n+1}$
and
$F_n\subseteq F_{n+1}$
and
 $\vert F_{n+1}\setminus F_n\vert \leq 1$
;
$\vert F_{n+1}\setminus F_n\vert \leq 1$
; -
(b)
 $\eta _0 (0)=0$
,
$\eta _0 (0)=0$
,
 $\eta _1(0)=1$
,
$\eta _1(0)=1$
,
 $\forall \beta \in F_n\quad \eta _n(\beta )\leq \eta _{n+1}(\beta )\leq \eta _n(\beta )+1$
and there is precisely one
$\forall \beta \in F_n\quad \eta _n(\beta )\leq \eta _{n+1}(\beta )\leq \eta _n(\beta )+1$
and there is precisely one
 $\beta \in F_{n+1}$
, which we call the active coordinate of
$\beta \in F_{n+1}$
, which we call the active coordinate of
 $F_{n+1}$
, such that
$F_{n+1}$
, such that
 $\eta _{n+1}(\beta )=\eta _n(\beta )+1$
in case
$\eta _{n+1}(\beta )=\eta _n(\beta )+1$
in case
 $\beta \in F_n$
, and
$\beta \in F_n$
, and
 $\eta _{n+1}(\beta )=0$
in case
$\eta _{n+1}(\beta )=0$
in case
 $\beta \not \in F_n$
; we also call
$\beta \not \in F_n$
; we also call
 $0\in F_0$
active;
$0\in F_0$
active; -
(c)
 $\forall \beta \in F_n\,\exists m \quad \eta _m(\beta )\geq n$
;
$\forall \beta \in F_n\,\exists m \quad \eta _m(\beta )\geq n$
; -
(d)
 $\bigcup \left \lbrace F_n:n<\omega \right \rbrace =\bigcup \left \lbrace \mathrm {{supp}}(p_n):n<\omega \right \rbrace $
;
$\bigcup \left \lbrace F_n:n<\omega \right \rbrace =\bigcup \left \lbrace \mathrm {{supp}}(p_n):n<\omega \right \rbrace $
; -
(e)
 $p_{n+1}\leq _{F_n, \eta _n} p_n.$
$p_{n+1}\leq _{F_n, \eta _n} p_n.$
(3) Every fusion sequence
![]() $\langle (p_n,F_n,\eta _n): n<\omega \rangle $
determines its fusion limit
$\langle (p_n,F_n,\eta _n): n<\omega \rangle $
determines its fusion limit
in
![]() $P_\alpha $
. Clearly,
$P_\alpha $
. Clearly,
![]() $\mathrm {{supp}}(p_\omega ) =\bigcup \left \lbrace F_n:n<\omega \right \rbrace $
.
$\mathrm {{supp}}(p_\omega ) =\bigcup \left \lbrace F_n:n<\omega \right \rbrace $
.
(4) For every
![]() $f\in \mathbb {SI}$
and
$f\in \mathbb {SI}$
and
![]() $s\in 2^{<\omega }$
we have defined
$s\in 2^{<\omega }$
we have defined
![]() $f^{s}\in \mathbb {SI}$
(see Definition 2.1(1)). If
$f^{s}\in \mathbb {SI}$
(see Definition 2.1(1)). If
![]() $(p,F,\eta ) $
is a fusion condition, for
$(p,F,\eta ) $
is a fusion condition, for
![]() $\sigma \in \prod \limits _{\beta \in F} \, ^{\eta (\beta )}2$
we define
$\sigma \in \prod \limits _{\beta \in F} \, ^{\eta (\beta )}2$
we define
![]() $p\ast \sigma \in P_\alpha $
as follows: For every
$p\ast \sigma \in P_\alpha $
as follows: For every
![]() $\beta \in F$
let
$\beta \in F$
let
![]() $(p\ast \sigma )(\beta )$
a
$(p\ast \sigma )(\beta )$
a
![]() $P_\beta $
-name for a condition in
$P_\beta $
-name for a condition in
![]() $\mathbb {SI}$
such that
$\mathbb {SI}$
such that
For every
![]() $\beta \in \alpha \setminus F$
let
$\beta \in \alpha \setminus F$
let
![]() $(p\ast \sigma )(\beta )= p(\beta )$
.
$(p\ast \sigma )(\beta )= p(\beta )$
.
(5) For
![]() $\beta \in \,\mathrm {supp}(p_\omega )$
let
$\beta \in \,\mathrm {supp}(p_\omega )$
let
![]() $Z(\beta )=Z(\bar S, \beta )$
denote the set
$Z(\beta )=Z(\bar S, \beta )$
denote the set
Clearly
![]() $\langle Z(\beta ):\beta \in \, \mathrm {supp}(p_\omega )\rangle $
is a partition of
$\langle Z(\beta ):\beta \in \, \mathrm {supp}(p_\omega )\rangle $
is a partition of
![]() $\omega $
into infinite sets.
$\omega $
into infinite sets.
(6) For
![]() $\beta \in \,\mathrm {supp}(p_\omega )$
, the increasing bijection between
$\beta \in \,\mathrm {supp}(p_\omega )$
, the increasing bijection between
![]() $Z(\beta ) $
and
$Z(\beta ) $
and
![]() $\mathrm {com}(p_\omega (\beta ))$
will be denoted by the
$\mathrm {com}(p_\omega (\beta ))$
will be denoted by the
![]() $P_\beta $
-name
$P_\beta $
-name
![]() $\dot {c}(p_\omega , \beta )$
.
$\dot {c}(p_\omega , \beta )$
.
Remark 2.1. (1) The demand
![]() $F_0=F_1= \left \lbrace 0\right \rbrace $
and
$F_0=F_1= \left \lbrace 0\right \rbrace $
and
![]() $F_2=\lbrace 0,1\rbrace $
in Definition 2.2(2)(a) is only to avoid having to consider several cases in some proofs below.
$F_2=\lbrace 0,1\rbrace $
in Definition 2.2(2)(a) is only to avoid having to consider several cases in some proofs below.
(2) If
![]() $(p,F,\eta )$
is a fusion condition then
$(p,F,\eta )$
is a fusion condition then
 $$ \begin{align*}\langle p\ast \sigma: \sigma\in \prod\limits_{\beta\in F} \, ^{\eta(\beta)}2\rangle\end{align*} $$
$$ \begin{align*}\langle p\ast \sigma: \sigma\in \prod\limits_{\beta\in F} \, ^{\eta(\beta)}2\rangle\end{align*} $$
is a (finite) maximal antichain below p.
(3) If
![]() $\bar {S} =\langle (p_n,F_n,\eta _n): n<\omega \rangle $
is a fusion sequence with limit
$\bar {S} =\langle (p_n,F_n,\eta _n): n<\omega \rangle $
is a fusion sequence with limit
![]() $p_\omega $
, then
$p_\omega $
, then
 $$ \begin{align*}\langle p_{n+1}\ast \sigma: \sigma\in \prod\limits_{\beta\in F_n} \, ^{\eta_n(\beta)+1}2\rangle\end{align*} $$
$$ \begin{align*}\langle p_{n+1}\ast \sigma: \sigma\in \prod\limits_{\beta\in F_n} \, ^{\eta_n(\beta)+1}2\rangle\end{align*} $$
is a maximal antichain below
![]() $p_{n+1}$
of size
$p_{n+1}$
of size
![]() $2^{n+1}$
and it induces a maximal antichain
$2^{n+1}$
and it induces a maximal antichain
![]() $A_{n+1}(\bar {S})$
below
$A_{n+1}(\bar {S})$
below
![]() $p_\omega $
of the same size, as
$p_\omega $
of the same size, as
such that every member of
![]() $A_{n}(\bar {S})$
gets refined by two members of
$A_{n}(\bar {S})$
gets refined by two members of
![]() $A_{n+1}(\bar {S})$
, where we let
$A_{n+1}(\bar {S})$
, where we let
![]() $A_0(\bar S)= \left \lbrace p_\omega \right \rbrace $
. Hence we naturally enumerate
$A_0(\bar S)= \left \lbrace p_\omega \right \rbrace $
. Hence we naturally enumerate
![]() $A_n(\bar {S})$
by
$A_n(\bar {S})$
by
![]() $\langle a^s: s\in \,^{n}2\rangle $
such that
$\langle a^s: s\in \,^{n}2\rangle $
such that
![]() $a^{s^{\smallfrown }0}$
,
$a^{s^{\smallfrown }0}$
,
![]() $a^{s^{\smallfrown }1}$
are the two members of
$a^{s^{\smallfrown }1}$
are the two members of
![]() $A_{n+1}(\bar {S})$
below
$A_{n+1}(\bar {S})$
below
![]() $a^s$
and, moreover, if
$a^s$
and, moreover, if
![]() $\gamma $
is the active coordinate of
$\gamma $
is the active coordinate of
![]() $F_n$
, thus
$F_n$
, thus
![]() $n\in Z(\gamma )$
, then
$n\in Z(\gamma )$
, then
![]() $a^{s^{\smallfrown }i}=p_\omega \ast \sigma $
for some
$a^{s^{\smallfrown }i}=p_\omega \ast \sigma $
for some
![]() $\sigma \in \prod \limits _{\beta \in F_n} \, ^{\eta _n(\beta )+1}2$
with the last digit of
$\sigma \in \prod \limits _{\beta \in F_n} \, ^{\eta _n(\beta )+1}2$
with the last digit of
![]() $\sigma (\gamma )$
being i.
$\sigma (\gamma )$
being i.
Definition 2.3. Let
![]() $\dot y$
be a
$\dot y$
be a
![]() $P_\alpha $
-name for an element of
$P_\alpha $
-name for an element of
![]() $\omega $
and
$\omega $
and
![]() $(p,F,\eta )$
a fusion condition. We say that
$(p,F,\eta )$
a fusion condition. We say that
![]() $(p,F,\eta )$
weakly decides
$(p,F,\eta )$
weakly decides
![]() $\dot y$
if for every
$\dot y$
if for every
![]() $\sigma \in \prod \limits _{\beta \in F} \, ^{\eta (\beta )+1}2$
,
$\sigma \in \prod \limits _{\beta \in F} \, ^{\eta (\beta )+1}2$
,
![]() $p\ast \sigma $
decides
$p\ast \sigma $
decides
![]() $\dot y$
.
$\dot y$
.
The following lemma is well-known (e.g., see [Reference Kuiper and Spinas5, Lemma 7.6] where it is proved for
![]() $\mathbb {U}_k)$
.
$\mathbb {U}_k)$
.
Lemma 2.1. Suppose
![]() $\Vdash _{P_\alpha } \, \dot {x}\in \omega ^\omega $
and
$\Vdash _{P_\alpha } \, \dot {x}\in \omega ^\omega $
and
![]() $p\in P_\alpha $
. There exists a fusion sequence
$p\in P_\alpha $
. There exists a fusion sequence
![]() $\langle (p_n,F_n,\eta _n): n<\omega \rangle $
in
$\langle (p_n,F_n,\eta _n): n<\omega \rangle $
in
![]() $ P_\alpha $
such that the following hold:
$ P_\alpha $
such that the following hold:
-
(1)
 $p_0= p$
;
$p_0= p$
; -
(2)
 $(p_{n}, F_{n},\eta _{n})$
weakly decides
$(p_{n}, F_{n},\eta _{n})$
weakly decides
 $\dot {x}\upharpoonright n$
, and hence, for every
$\dot {x}\upharpoonright n$
, and hence, for every
 $n<\omega $
,
$n<\omega $
,
 $(p_\omega , F_{n},\eta _{n})$
weakly decides
$(p_\omega , F_{n},\eta _{n})$
weakly decides
 $\dot {x}\upharpoonright n$
.
$\dot {x}\upharpoonright n$
.
3 The Grigorieff dichotomy
Definition 3.1. Let
![]() $\alpha \leq \omega _2$
and suppose that
$\alpha \leq \omega _2$
and suppose that
![]() $P_\alpha $
is a CS-iteration of
$P_\alpha $
is a CS-iteration of
![]() $\mathbb {SI}$
,
$\mathbb {SI}$
,
![]() $\dot {x}$
is a
$\dot {x}$
is a
![]() $P_\alpha $
-name such that
$P_\alpha $
-name such that
![]() $\Vdash _{P_\alpha }\, \dot x\in 2^\omega \setminus \mathbf {V}$
and
$\Vdash _{P_\alpha }\, \dot x\in 2^\omega \setminus \mathbf {V}$
and
![]() $p\in P_\alpha $
. By
$p\in P_\alpha $
. By
![]() $\dot x\left [ p\right ] $
we denote the longest
$\dot x\left [ p\right ] $
we denote the longest
![]() $t\in \, ^{< \omega }2$
such that
$t\in \, ^{< \omega }2$
such that
Following Grigorieff [Reference Grigorieff3] we say that
![]() $k<\omega $
is indifferent to
$k<\omega $
is indifferent to
![]() $p, \dot {x}$
, if
$p, \dot {x}$
, if
![]() $k\in \,\mathrm {com}(p(0))$
and there is no
$k\in \,\mathrm {com}(p(0))$
and there is no
![]() $q\leq p$
such that
$q\leq p$
such that
![]() $k\in \,\mathrm {com}(q(0))$
and
$k\in \,\mathrm {com}(q(0))$
and
where
We have the following Grigorieff dichotomy: Either (G1) or (G2) holds, where
-
(G1)
 $\forall p\exists q\leq p\forall r\leq q \forall k \quad k$
is not indifferent to
$\forall p\exists q\leq p\forall r\leq q \forall k \quad k$
is not indifferent to
 $r, \dot {x}$
;
$r, \dot {x}$
; -
(G2)
 $\exists p\forall q\leq p\exists r\leq q\exists k\quad k$
is indifferent to
$\exists p\forall q\leq p\exists r\leq q\exists k\quad k$
is indifferent to
 $r,\dot {x} $
.
$r,\dot {x} $
.
The following lemma, whose prototype is [Reference Grigorieff3, Lemma 4.7], shows that if
![]() $\dot x$
is a name for a new real, then (G1) must hold.
$\dot x$
is a name for a new real, then (G1) must hold.
Lemma 3.1. Suppose
![]() $\Vdash _{P_\alpha } \,\dot {x}\in \omega ^\omega $
and
$\Vdash _{P_\alpha } \,\dot {x}\in \omega ^\omega $
and
![]() $p\in P_\alpha $
witnesses that (G2) of Grigorieff’s dichotomy holds. Then
$p\in P_\alpha $
witnesses that (G2) of Grigorieff’s dichotomy holds. Then
![]() $p \Vdash _{P_\alpha } \,\dot {x}\in \mathbf {V}.$
$p \Vdash _{P_\alpha } \,\dot {x}\in \mathbf {V}.$
Proof. We construct a fusion sequence
![]() $\langle (p_n, F_n, \eta _n): n<\omega \rangle $
in
$\langle (p_n, F_n, \eta _n): n<\omega \rangle $
in
![]() $P_\alpha $
and families
$P_\alpha $
and families
![]() $\langle n_k:k<\omega \rangle $
,
$\langle n_k:k<\omega \rangle $
,
![]() $\langle j_k:k<\omega \rangle $
and
$\langle j_k:k<\omega \rangle $
and
![]() $\langle \xi _n: n<\omega \rangle $
such that
$\langle \xi _n: n<\omega \rangle $
such that
![]() $p_0\leq p$
and for every
$p_0\leq p$
and for every
![]() $n<\omega $
the following hold:
$n<\omega $
the following hold:
-
(1)
 $\langle n_k:k<\omega \rangle $
increasingly enumerates
$\langle n_k:k<\omega \rangle $
increasingly enumerates
 $Z(0)$
(hence
$Z(0)$
(hence
 $n_0=0$
and
$n_0=0$
and
 $n_1=1$
);
$n_1=1$
); -
(2) if
 $Z(0)\cap n= \lbrace n_0,...,n_{k-1}\rbrace $
, then
$Z(0)\cap n= \lbrace n_0,...,n_{k-1}\rbrace $
, then
 $\lbrace j_0<...<j_{k-1}\rbrace $
is an initial segment of com
$\lbrace j_0<...<j_{k-1}\rbrace $
is an initial segment of com
 $(p_n(0))$
and
$(p_n(0))$
and
 $j_\ell $
is indifferent to
$j_\ell $
is indifferent to
 $p_{n}, \dot {x}$
for every
$p_{n}, \dot {x}$
for every
 $\ell < k$
;
$\ell < k$
; -
(3) if
 $n=n_k$
then
$n=n_k$
then
 $\lbrace j_0<...<j_{k}\rbrace $
is an initial segment of com
$\lbrace j_0<...<j_{k}\rbrace $
is an initial segment of com
 $(p_n(0))$
and
$(p_n(0))$
and
 $j_\ell $
is indifferent to
$j_\ell $
is indifferent to
 $p_{n}, \dot {x}$
for every
$p_{n}, \dot {x}$
for every
 $\ell \leq k$
;
$\ell \leq k$
; -
(4)
 $\xi _n\in \, ^{n}2$
and
$\xi _n\in \, ^{n}2$
and
 $p_{n} \Vdash _{P_\alpha } \, \dot {x}\upharpoonright n=\xi _{n}$
.
$p_{n} \Vdash _{P_\alpha } \, \dot {x}\upharpoonright n=\xi _{n}$
.
We present the first three steps of the recursive construction in detail to make clear the crucial arguments in a simple situation. After that we shall give the general step.
We apply (G2) and obtain
![]() $p_0\leq p$
and
$p_0\leq p$
and
![]() $j_0\in \,\mathrm {com}(p_0(0))$
such that
$j_0\in \,\mathrm {com}(p_0(0))$
such that
![]() $j_0$
is indifferent to
$j_0$
is indifferent to
![]() $p_0, \dot {x}$
. Wlog we may assume
$p_0, \dot {x}$
. Wlog we may assume
![]() $j_0=\min ( \mathrm {com}(p_0(0)))$
. Letting
$j_0=\min ( \mathrm {com}(p_0(0)))$
. Letting
![]() $\xi _0=\emptyset $
, (2), (3), and (4) hold for
$\xi _0=\emptyset $
, (2), (3), and (4) hold for
![]() $n=n_0=0$
.
$n=n_0=0$
.
By Lemma 2.1, we can choose
![]() $q_1\leq _{F_0,\eta _0}p_0$
(hence
$q_1\leq _{F_0,\eta _0}p_0$
(hence
![]() $j_0\in \,\mathrm {com}(q_1(0))$
) such that
$j_0\in \,\mathrm {com}(q_1(0))$
) such that
![]() $(q_1, F_0, \eta _0)$
weakly decides
$(q_1, F_0, \eta _0)$
weakly decides
![]() $\dot {x}\upharpoonright 1$
. Note that then
$\dot {x}\upharpoonright 1$
. Note that then
![]() $q_1$
even decides
$q_1$
even decides
![]() $\dot x\upharpoonright 1$
, say as
$\dot x\upharpoonright 1$
, say as
![]() $\xi _1$
, as otherwise we had
$\xi _1$
, as otherwise we had
where
![]() $\sigma _i=\langle \langle i\rangle \rangle $
, which contradicts the indifference of
$\sigma _i=\langle \langle i\rangle \rangle $
, which contradicts the indifference of
![]() $j_0$
(note that
$j_0$
(note that
![]() $q_1^{(j_0,i)} = q_1\ast \sigma _i$
). By (G2) we can find
$q_1^{(j_0,i)} = q_1\ast \sigma _i$
). By (G2) we can find
![]() $p_1\leq _{F_0,\eta _0} q_1$
and
$p_1\leq _{F_0,\eta _0} q_1$
and
![]() $j_1$
such that
$j_1$
such that
![]() $j_1$
is indifferent to
$j_1$
is indifferent to
![]() $p_1\ast \sigma _0, \dot {x}$
. Hence
$p_1\ast \sigma _0, \dot {x}$
. Hence
![]() $j_1>j_0$
and wlog we may assume that
$j_1>j_0$
and wlog we may assume that
![]() $j_1$
is the second member of com
$j_1$
is the second member of com
![]() $(p_1(0))$
.
$(p_1(0))$
.
We claim that
![]() $j_1$
is indifferent even to
$j_1$
is indifferent even to
![]() $p_1,\dot {x}$
, and hence (2), (3), and (4) hold for
$p_1,\dot {x}$
, and hence (2), (3), and (4) hold for
![]() $n=n_1=1$
. Indeed, otherwise we could find
$n=n_1=1$
. Indeed, otherwise we could find
![]() $q\leq _{F_1,\eta _1} p_1$
such that, letting
$q\leq _{F_1,\eta _1} p_1$
such that, letting
![]() $\sigma _{ij}= \langle \langle i,j\rangle \rangle $
(recall that by Definition 2.2(2)
$\sigma _{ij}= \langle \langle i,j\rangle \rangle $
(recall that by Definition 2.2(2)
![]() $F_1=\left \lbrace 0\right \rbrace $
and
$F_1=\left \lbrace 0\right \rbrace $
and
![]() $\eta _1(0)=1$
),
$\eta _1(0)=1$
),
say
for some m. Wlog we may assume that
![]() $(q,F_1,\eta _1)$
weakly decides
$(q,F_1,\eta _1)$
weakly decides
![]() $\dot {x}\upharpoonright m+1$
. By the indifference of
$\dot {x}\upharpoonright m+1$
. By the indifference of
![]() $j_1$
to
$j_1$
to
![]() $q\ast \sigma _0, \dot {x}$
, as above we conclude that
$q\ast \sigma _0, \dot {x}$
, as above we conclude that
![]() $q\ast \sigma _0$
decides
$q\ast \sigma _0$
decides
![]() $\dot {x}(m)$
. But now we can choose j such that
$\dot {x}(m)$
. But now we can choose j such that
contradicting that
![]() $j_0$
is indifferent to
$j_0$
is indifferent to
![]() $p_0, \dot {x}$
.
$p_0, \dot {x}$
.
In order to find
![]() $p_2$
as desired we first choose
$p_2$
as desired we first choose
![]() $q_2 \leq _{F_1,\eta _1} p_1$
such that
$q_2 \leq _{F_1,\eta _1} p_1$
such that
![]() $(q_2, F_2, \eta _2)$
weakly decides
$(q_2, F_2, \eta _2)$
weakly decides
![]() $\dot {x}(1) $
. Again we claim that
$\dot {x}(1) $
. Again we claim that
![]() $q_2$
even decides
$q_2$
even decides
![]() $\dot {x}(1) $
. Otherwise, as each
$\dot {x}(1) $
. Otherwise, as each
![]() $ \sigma \in \prod \limits _{\beta \in F_2} \, ^{\eta _2(\beta )+1}2$
is of the form
$ \sigma \in \prod \limits _{\beta \in F_2} \, ^{\eta _2(\beta )+1}2$
is of the form
![]() $\sigma _{ijk}=\langle \langle i,j\rangle , \langle k\rangle \rangle $
, we find distinct
$\sigma _{ijk}=\langle \langle i,j\rangle , \langle k\rangle \rangle $
, we find distinct
![]() $\sigma =\sigma _{ijk}$
and
$\sigma =\sigma _{ijk}$
and
![]() $\sigma '=\sigma _{i'j'k'}$
such that
$\sigma '=\sigma _{i'j'k'}$
such that
![]() $q_2\ast \sigma $
and
$q_2\ast \sigma $
and
![]() $q_2\ast \sigma '$
force different values to
$q_2\ast \sigma '$
force different values to
![]() $\dot {x}(1)$
, say x and
$\dot {x}(1)$
, say x and
![]() $x'$
. The most interesting case is
$x'$
. The most interesting case is
![]() $\langle i,j\rangle =\langle i',j'\rangle $
and hence
$\langle i,j\rangle =\langle i',j'\rangle $
and hence
![]() $k\ne k'$
. By indifference of
$k\ne k'$
. By indifference of
![]() $j_1$
we have that, letting
$j_1$
we have that, letting
![]() $\sigma " = \langle \langle i,1-j\rangle , k\rangle $
,
$\sigma " = \langle \langle i,1-j\rangle , k\rangle $
,
![]() $q_2\ast \sigma "$
decides
$q_2\ast \sigma "$
decides
![]() $\dot {x}(1)$
as x. Now we can define
$\dot {x}(1)$
as x. Now we can define
![]() $r\leq _{F_0,\eta _0} q_2 \ast \langle i\rangle $
such that
$r\leq _{F_0,\eta _0} q_2 \ast \langle i\rangle $
such that
![]() $r\ast \langle 1-j\rangle $
decides
$r\ast \langle 1-j\rangle $
decides
![]() $\dot {x}(1)$
as x while
$\dot {x}(1)$
as x while
![]() $r\ast \langle j\rangle $
decides
$r\ast \langle j\rangle $
decides
![]() $\dot {x}(1)$
as
$\dot {x}(1)$
as
![]() $x'$
, which contradicts the indifference of
$x'$
, which contradicts the indifference of
![]() $j_1$
. Indeed, let r such that
$j_1$
. Indeed, let r such that
![]() $r(0)= (q_2\ast \langle i\rangle )(0)$
(which is the same thing as
$r(0)= (q_2\ast \langle i\rangle )(0)$
(which is the same thing as
![]() $q_2(0)^{\langle i\rangle } $
) and
$q_2(0)^{\langle i\rangle } $
) and
 $$\begin{align*}r \upharpoonright \left[ 1,\alpha\right) = \left\{\begin{array}{cl} {q_2(1)^{\langle k\rangle} }^{\smallfrown} q_2\upharpoonright \left[ 2,\alpha\right)\!, & {\mathrm{if}}\; r(0)^{\langle i, 1-j\rangle} \;\mathrm{(belongs \; to \;the \; generic\;} G(0))\\ {q_2(1)^{\langle k'\rangle} }^{\smallfrown} q_2\upharpoonright \left[ 2,\alpha\right)\!, & {\mathrm{otherwise.}} \end{array} \right.\end{align*}$$
$$\begin{align*}r \upharpoonright \left[ 1,\alpha\right) = \left\{\begin{array}{cl} {q_2(1)^{\langle k\rangle} }^{\smallfrown} q_2\upharpoonright \left[ 2,\alpha\right)\!, & {\mathrm{if}}\; r(0)^{\langle i, 1-j\rangle} \;\mathrm{(belongs \; to \;the \; generic\;} G(0))\\ {q_2(1)^{\langle k'\rangle} }^{\smallfrown} q_2\upharpoonright \left[ 2,\alpha\right)\!, & {\mathrm{otherwise.}} \end{array} \right.\end{align*}$$
The other cases, i.e.,
![]() $\langle i,j\rangle \ne \langle i',j'\rangle $
, are similar.
$\langle i,j\rangle \ne \langle i',j'\rangle $
, are similar.
Now we can let
![]() $p_2=q_2$
and
$p_2=q_2$
and
![]() $\xi _2$
is what
$\xi _2$
is what
![]() $q_2$
decides about
$q_2$
decides about
![]() $\dot {x}\upharpoonright 2$
. Then clearly (2) and (4) hold for
$\dot {x}\upharpoonright 2$
. Then clearly (2) and (4) hold for
![]() $n=2$
and (3) does not apply.
$n=2$
and (3) does not apply.
Now we consider the general recursive step, where we have to apply essentially the same arguments we have seen above. Suppose that
![]() $(p_0, F_0, \eta _0), \dots , (p_n,F_n,\eta _n)$
,
$(p_0, F_0, \eta _0), \dots , (p_n,F_n,\eta _n)$
,
![]() $\xi _0,\dots ,\xi _n$
for
$\xi _0,\dots ,\xi _n$
for
![]() $n\geq 2$
have been constructed for some
$n\geq 2$
have been constructed for some
![]() $n<\omega $
together with some initial segment
$n<\omega $
together with some initial segment
![]() $\langle j_\ell :\ell \leq k\rangle $
of com
$\langle j_\ell :\ell \leq k\rangle $
of com
![]() $(p_n(0))$
, where k is such that
$(p_n(0))$
, where k is such that
![]() $Z(0)\cap (n+1) =\lbrace n_0<...<n_k\rbrace $
such that
$Z(0)\cap (n+1) =\lbrace n_0<...<n_k\rbrace $
such that
and every
![]() $j_\ell $
(
$j_\ell $
(
![]() $\ell \leq k$
) is indifferent to
$\ell \leq k$
) is indifferent to
![]() $p_n, \dot {x}$
.
$p_n, \dot {x}$
.
We have to distinguish two cases:
Case 1:
![]() $n+1\in Z(0)$
, thus
$n+1\in Z(0)$
, thus
![]() $n+1 = n_{k+1}$
and clearly
$n+1 = n_{k+1}$
and clearly
![]() $n>k$
,
$n>k$
,
![]() $\eta _n(0)= k$
and
$\eta _n(0)= k$
and
![]() $\eta _{n+1}(0)=k+1$
.
$\eta _{n+1}(0)=k+1$
.
Fix some
![]() $ \tau \in \prod \limits _{\beta \in F_n} \, ^{\eta _n(\beta )+1}2$
. By (G2) and Lemma 2.1 we can find
$ \tau \in \prod \limits _{\beta \in F_n} \, ^{\eta _n(\beta )+1}2$
. By (G2) and Lemma 2.1 we can find
![]() $p_{n+1}\leq _{F_n,\eta _n} p_n$
and
$p_{n+1}\leq _{F_n,\eta _n} p_n$
and
![]() $j_{k+1}$
such that
$j_{k+1}$
such that
![]() $j_{k+1}$
is indifferent to
$j_{k+1}$
is indifferent to
![]() $p_{n+1}\ast \tau , \dot {x}$
and
$p_{n+1}\ast \tau , \dot {x}$
and
![]() $p_{n+1}$
weakly decides
$p_{n+1}$
weakly decides
![]() $\dot {x}(n)$
. Then clearly
$\dot {x}(n)$
. Then clearly
![]() $j_{k+1}>j_k$
. Wlog we may assume that
$j_{k+1}>j_k$
. Wlog we may assume that
![]() $\lbrace j_0,...,j_{k+1}\rbrace $
is an initial segment of com
$\lbrace j_0,...,j_{k+1}\rbrace $
is an initial segment of com
![]() $(p_{n+1}(0))$
.
$(p_{n+1}(0))$
.
At first we show that
![]() $p_{n+1}$
even decides
$p_{n+1}$
even decides
![]() $\dot x(n)$
(and hence
$\dot x(n)$
(and hence
![]() $\dot {x}\upharpoonright n+1$
). Then a similar argument together with the one above showing indifference of
$\dot {x}\upharpoonright n+1$
). Then a similar argument together with the one above showing indifference of
![]() $j_1$
to
$j_1$
to
![]() $p_1,\dot {x}$
will prove that
$p_1,\dot {x}$
will prove that
![]() $j_{k+1}$
is even indifferent to
$j_{k+1}$
is even indifferent to
![]() $p_{n+1},\dot {x}$
.
$p_{n+1},\dot {x}$
.
For
![]() $ \sigma \in \prod \limits _{\beta \in F_n} \, ^{\eta _n(\beta )+1}2$
let
$ \sigma \in \prod \limits _{\beta \in F_n} \, ^{\eta _n(\beta )+1}2$
let
![]() $x_\sigma $
such that
$x_\sigma $
such that
For
![]() $\sigma , \sigma ' \in \prod \limits _{\beta \in F_n} \, ^{\eta _n(\beta )+1}2$
let
$\sigma , \sigma ' \in \prod \limits _{\beta \in F_n} \, ^{\eta _n(\beta )+1}2$
let
![]() $\mathit {s}=\mathit {s}(\sigma , \sigma ')$
be the size of the set
$\mathit {s}=\mathit {s}(\sigma , \sigma ')$
be the size of the set
We shall prove
![]() $x_\sigma =x_{\sigma '}$
by induction on s. Suppose first that
$x_\sigma =x_{\sigma '}$
by induction on s. Suppose first that
![]() $\mathit {s}(\sigma , \sigma ')=0$
(thus
$\mathit {s}(\sigma , \sigma ')=0$
(thus
![]() $\sigma (0)=\sigma '(0)$
) and
$\sigma (0)=\sigma '(0)$
) and
![]() $\sigma \ne \sigma '$
. Let
$\sigma \ne \sigma '$
. Let
![]() $ \sigma ^{\prime }_1$
be defined as follows: If
$ \sigma ^{\prime }_1$
be defined as follows: If
![]() $(\sigma (0))(0)=i$
,
$(\sigma (0))(0)=i$
,
![]() $\sigma _1'$
equals
$\sigma _1'$
equals
![]() $\sigma '$
except for
$\sigma '$
except for
![]() $(\sigma _1'(0))(0)=1-i$
.
$(\sigma _1'(0))(0)=1-i$
.
As
![]() $j_0$
is indifferent to
$j_0$
is indifferent to
![]() $p_{n+1}$
we must have
$p_{n+1}$
we must have
![]() $x_{\sigma '}=x_{\sigma ^{\prime }_1}$
. Hence if we had
$x_{\sigma '}=x_{\sigma ^{\prime }_1}$
. Hence if we had
![]() $x_\sigma \ne x_{\sigma '}$
, then also
$x_\sigma \ne x_{\sigma '}$
, then also
![]() $x_\sigma \ne x_{\sigma ^{\prime }_1}$
. But this leads to a contradiction to the indifference of
$x_\sigma \ne x_{\sigma ^{\prime }_1}$
. But this leads to a contradiction to the indifference of
![]() $j_0$
, as follows: Define
$j_0$
, as follows: Define
![]() $r\in P_\alpha $
such that
$r\in P_\alpha $
such that
(hence
![]() $j_0=\min (\mathrm {com}(r(0)))$
and
$j_0=\min (\mathrm {com}(r(0)))$
and
![]() $r(0)$
does not change if
$r(0)$
does not change if
![]() $\sigma $
is replaced by
$\sigma $
is replaced by
![]() $\sigma '$
) and, for
$\sigma '$
) and, for
![]() $j<2$
,
$j<2$
,
where
![]() $\tau _i =\sigma \upharpoonright F_n\setminus \left \lbrace 0\right \rbrace $
and
$\tau _i =\sigma \upharpoonright F_n\setminus \left \lbrace 0\right \rbrace $
and
![]() $\tau _{1-i}= \sigma ' \upharpoonright F_n\setminus \left \lbrace 0\right \rbrace $
. Clearly
$\tau _{1-i}= \sigma ' \upharpoonright F_n\setminus \left \lbrace 0\right \rbrace $
. Clearly
![]() $r\leq p_n$
, but
$r\leq p_n$
, but
a contradiction.
Now suppose
![]() $\mathit {s}(\sigma , \sigma ')=m+1$
and for
$\mathit {s}(\sigma , \sigma ')=m+1$
and for
![]() $\mathit {s}\leq m$
the claim is true. Let
$\mathit {s}\leq m$
the claim is true. Let
![]() $\ell ^*\leq \eta _n(0)$
(hence
$\ell ^*\leq \eta _n(0)$
(hence
![]() $\ell ^*\leq k$
) be maximal such that
$\ell ^*\leq k$
) be maximal such that
![]() $(\sigma (0))(\ell ^*)\ne (\sigma '(0))(\ell ^*)$
. Now define
$(\sigma (0))(\ell ^*)\ne (\sigma '(0))(\ell ^*)$
. Now define
![]() $ \sigma ^{\prime }_1$
as follows: If
$ \sigma ^{\prime }_1$
as follows: If
![]() $(\sigma (0))(\ell ^*)=i$
let
$(\sigma (0))(\ell ^*)=i$
let
![]() $\sigma _1'$
be equal to
$\sigma _1'$
be equal to
![]() $\sigma '$
except for
$\sigma '$
except for
![]() $(\sigma _1'(0))(\ell ^*)=i$
.
$(\sigma _1'(0))(\ell ^*)=i$
.
By the indifference of
![]() $j_{\ell ^*}$
we must have
$j_{\ell ^*}$
we must have
![]() $x_{\sigma '}=x_{\sigma ^{\prime }_1}$
. By the inductive hypothesis we have
$x_{\sigma '}=x_{\sigma ^{\prime }_1}$
. By the inductive hypothesis we have
![]() $x_\sigma = x_{\sigma ^{\prime }_1}$
. Hence we conclude
$x_\sigma = x_{\sigma ^{\prime }_1}$
. Hence we conclude
![]() $x_\sigma = x_{\sigma ^{\prime }_{1}} =x_{\sigma '}$
and thus
$x_\sigma = x_{\sigma ^{\prime }_{1}} =x_{\sigma '}$
and thus
![]() $p_{n+1}$
decides
$p_{n+1}$
decides
![]() $\dot {x}\upharpoonright n+1$
as claimed. Denote this decision by
$\dot {x}\upharpoonright n+1$
as claimed. Denote this decision by
![]() $\xi _{n+1}$
. Then clearly (2), (3), and (4) hold for
$\xi _{n+1}$
. Then clearly (2), (3), and (4) hold for
![]() $n+1$
.
$n+1$
.
Now let us sketch why
![]() $j_{k+1}$
is indifferent to
$j_{k+1}$
is indifferent to
![]() $p_{n+1},\dot {x}$
. Otherwise we could find
$p_{n+1},\dot {x}$
. Otherwise we could find
![]() $q\leq _{F_{n+1}, \eta _{n+1}}$
,
$q\leq _{F_{n+1}, \eta _{n+1}}$
,
![]() $\tau '\in \prod _{\beta \in F_n}\,^{\eta _n(\beta )+1}2$
and
$\tau '\in \prod _{\beta \in F_n}\,^{\eta _n(\beta )+1}2$
and
![]() $m<\omega $
such that
$m<\omega $
such that
![]() $\dot {x}\left [ q\ast \tau '\,^{\smallfrown }0 \right ] (m)\ne \dot {x}\left [ q\ast \tau '\,^{\smallfrown }1\right ] (m)$
and q weakly decides
$\dot {x}\left [ q\ast \tau '\,^{\smallfrown }0 \right ] (m)\ne \dot {x}\left [ q\ast \tau '\,^{\smallfrown }1\right ] (m)$
and q weakly decides
![]() $\dot {x}\upharpoonright m+1$
. Similarly as we showed above that
$\dot {x}\upharpoonright m+1$
. Similarly as we showed above that
![]() $p_{n+1}$
decides
$p_{n+1}$
decides
![]() $\dot {x}(n)$
, applying indifference of
$\dot {x}(n)$
, applying indifference of
![]() $j_{k+1}$
to
$j_{k+1}$
to
![]() $p_{n+1}\ast \tau $
, we can show that q even decides
$p_{n+1}\ast \tau $
, we can show that q even decides
![]() $\dot {x}(m)$
, which is a contradiction.
$\dot {x}(m)$
, which is a contradiction.
Case 2:
![]() $n+1\not \in Z(0)$
.
$n+1\not \in Z(0)$
.
Choose
![]() $p_{n+1}\leq _{F_n,\eta _n} p_n$
such that
$p_{n+1}\leq _{F_n,\eta _n} p_n$
such that
![]() $p_{n+1}$
weakly decides
$p_{n+1}$
weakly decides
![]() $\dot {x}(n)$
. Very similarly as in Case 1 we can show that
$\dot {x}(n)$
. Very similarly as in Case 1 we can show that
![]() $p_{n+1}$
even decides
$p_{n+1}$
even decides
![]() $\dot {x}(n)$
, hence also
$\dot {x}(n)$
, hence also
![]() $\dot {x}\upharpoonright n+1$
, and we denote this decision by
$\dot {x}\upharpoonright n+1$
, and we denote this decision by
![]() $\xi _{n+1}$
. Then clearly (2) and (4) hold for
$\xi _{n+1}$
. Then clearly (2) and (4) hold for
![]() $n+1$
and (3) does not apply.
$n+1$
and (3) does not apply.
By Lemma 3.1 we conclude that if
![]() $\dot x$
is a
$\dot x$
is a
![]() $P_\alpha $
-name for a new real, then (G1) of the Grigorieff dichotomy must hold. As Theorem 3.1 below will show, this enables us to find a very precise form of continuous reading of
$P_\alpha $
-name for a new real, then (G1) of the Grigorieff dichotomy must hold. As Theorem 3.1 below will show, this enables us to find a very precise form of continuous reading of
![]() $\dot x$
. The prototype of this result is [Reference Grigorieff3, Lemma 4.6].
$\dot x$
. The prototype of this result is [Reference Grigorieff3, Lemma 4.6].
The following definition was introduced in [Reference Kuiper and Spinas5] (see Definition 7.8).
Definition 3.2. Let
![]() $\dot {x}$
be a
$\dot {x}$
be a
![]() $P_\alpha $
-name for an element of
$P_\alpha $
-name for an element of
![]() $\omega ^\omega $
. We say that a fusion condition
$\omega ^\omega $
. We say that a fusion condition
![]() $(p,F,\eta )$
splits
$(p,F,\eta )$
splits
![]() $\dot x$
at
$\dot x$
at
![]() $\gamma \in F$
if for every
$\gamma \in F$
if for every
 $$ \begin{align*}\sigma\in \prod\limits_{\beta\in F\setminus \left\lbrace \gamma \right\rbrace } \, ^{\eta(\beta)+1}2\quad \mathrm{and }\quad s_0,s_1\in \, ^{(\eta(\gamma)+1)}2\end{align*} $$
$$ \begin{align*}\sigma\in \prod\limits_{\beta\in F\setminus \left\lbrace \gamma \right\rbrace } \, ^{\eta(\beta)+1}2\quad \mathrm{and }\quad s_0,s_1\in \, ^{(\eta(\gamma)+1)}2\end{align*} $$
with
![]() $s_0\upharpoonright \eta (\gamma )=s_1\upharpoonright \eta (\gamma )$
and
$s_0\upharpoonright \eta (\gamma )=s_1\upharpoonright \eta (\gamma )$
and
![]() $s_0(\eta (\gamma ))<s_1(\eta (\gamma ))$
,
$s_0(\eta (\gamma ))<s_1(\eta (\gamma ))$
,
Theorem 3.1. Suppose
![]() $p\in P_\alpha $
and
$p\in P_\alpha $
and
There exists a fusion sequence
![]() $\bar {S}=\langle (p_n,F_n,\eta _n):n<\omega \rangle $
below p such that for every n, if
$\bar {S}=\langle (p_n,F_n,\eta _n):n<\omega \rangle $
below p such that for every n, if
![]() $\gamma $
is the active coordinate of
$\gamma $
is the active coordinate of
![]() $F_{n}$
then
$F_{n}$
then
![]() $(p_{n}, F_{n}, \eta _{n})$
splits
$(p_{n}, F_{n}, \eta _{n})$
splits
![]() $\dot x$
at
$\dot x$
at
![]() $\gamma $
.
$\gamma $
.
Moreover, letting
![]() $A_n(\bar {S})$
and
$A_n(\bar {S})$
and
![]() $\langle a^s: s\in \, ^{n}2\rangle $
be defined as in Remark 2.1 and letting
$\langle a^s: s\in \, ^{n}2\rangle $
be defined as in Remark 2.1 and letting
![]() $t_s$
the longest common initial segment of
$t_s$
the longest common initial segment of
![]() $\dot {x}\left [ a^{s^{\smallfrown } 0}\right ] $
and
$\dot {x}\left [ a^{s^{\smallfrown } 0}\right ] $
and
![]() $\dot {x}\left [ a^{s^{\smallfrown } 1}\right ] $
, the following hold:
$\dot {x}\left [ a^{s^{\smallfrown } 1}\right ] $
, the following hold:
-
(0)
 $\dot {x}\left [ a^{s^{\smallfrown } 0}\right ] (\vert t_s\vert )\perp \dot {x}\left [ a^{s^{\smallfrown } 1}\right ](\vert t_s\vert )$
;
$\dot {x}\left [ a^{s^{\smallfrown } 0}\right ] (\vert t_s\vert )\perp \dot {x}\left [ a^{s^{\smallfrown } 1}\right ](\vert t_s\vert )$
; -
(1) if
 $\vert s\vert <\vert s'\vert $
then
$\vert s\vert <\vert s'\vert $
then
 $\vert t_s\vert < \vert t_{s'}\vert $
;
$\vert t_s\vert < \vert t_{s'}\vert $
; -
(2) if
 $\gamma $
is the active coordinate of
$\gamma $
is the active coordinate of
 $F_n$
and
$F_n$
and
 $s, s'\in \, ^{n}2 $
are such that we have
$s, s'\in \, ^{n}2 $
are such that we have $$ \begin{align*}s\upharpoonright n\setminus \bigcup \left\lbrace Z(\beta):\beta\geq \gamma\right\rbrace \ne s'\upharpoonright n\setminus \bigcup \left\lbrace Z(\beta):\beta\geq \gamma\right\rbrace\end{align*} $$
$$ \begin{align*}s\upharpoonright n\setminus \bigcup \left\lbrace Z(\beta):\beta\geq \gamma\right\rbrace \ne s'\upharpoonright n\setminus \bigcup \left\lbrace Z(\beta):\beta\geq \gamma\right\rbrace\end{align*} $$
 $\vert t_s\vert \ne \vert t_{s'}\vert $
. (For the definition of
$\vert t_s\vert \ne \vert t_{s'}\vert $
. (For the definition of
 $Z(\beta )$
see Definition 2.2(5).)
$Z(\beta )$
see Definition 2.2(5).)
Proof. Our recursive construction will guarantee that the following demand holds for every n:
-
(*) n If
 $\gamma $
is the active coordinate of
$\gamma $
is the active coordinate of
 $F_n$
then
$F_n$
then  $$ \begin{align*}p_n\upharpoonright \gamma \Vdash_{P_\gamma}\, \forall r\leq p_n \upharpoonright \left[ \gamma , \alpha\right)\forall k\quad k\mathrm{\; is \;not \; indifferent\; to\; } r,\dot{x}.\end{align*} $$
$$ \begin{align*}p_n\upharpoonright \gamma \Vdash_{P_\gamma}\, \forall r\leq p_n \upharpoonright \left[ \gamma , \alpha\right)\forall k\quad k\mathrm{\; is \;not \; indifferent\; to\; } r,\dot{x}.\end{align*} $$
For
![]() $(\ast )_n$
to make sense we use the well-known fact that the quotient forcing
$(\ast )_n$
to make sense we use the well-known fact that the quotient forcing
![]() $P_\alpha /\dot G_\gamma $
is again a CS-support iteration of
$P_\alpha /\dot G_\gamma $
is again a CS-support iteration of
![]() $\mathbb {SI}$
(see [Reference Baumgartner and Mathias1, Section 5]).
$\mathbb {SI}$
(see [Reference Baumgartner and Mathias1, Section 5]).
We have to find
![]() $p_0$
such that
$p_0$
such that
![]() $(p_0,F_0,\eta _0)$
splits
$(p_0,F_0,\eta _0)$
splits
![]() $\dot {x}$
at
$\dot {x}$
at
![]() $0$
. For this we first apply Lemma 3.1 and the assumption and conclude that (G2) of Grigorieff’s dichotomy fails below p, hence (G1) holds below p and we obtain
$0$
. For this we first apply Lemma 3.1 and the assumption and conclude that (G2) of Grigorieff’s dichotomy fails below p, hence (G1) holds below p and we obtain
![]() $ q$
as in (G1). Let
$ q$
as in (G1). Let
![]() $k=\min (\mathrm {com}(q(0)))$
. As k is not indifferent to
$k=\min (\mathrm {com}(q(0)))$
. As k is not indifferent to
![]() $q,\dot {x}$
we find
$q,\dot {x}$
we find
![]() $p_0\leq q$
as desired. By (G1) we also know that at every later stage
$p_0\leq q$
as desired. By (G1) we also know that at every later stage
![]() $n\in Z(0)$
we will have
$n\in Z(0)$
we will have
![]() $(\ast )_n$
.
$(\ast )_n$
.
Now suppose we have gotten
![]() $(p_0,F_0,\eta _0),...,(p_n,F_n,\eta _n)$
as desired such that
$(p_0,F_0,\eta _0),...,(p_n,F_n,\eta _n)$
as desired such that
![]() $(\ast )_m$
holds for every
$(\ast )_m$
holds for every
![]() $m\leq n$
.
$m\leq n$
.
Let
![]() $\gamma $
be the active coordinate of
$\gamma $
be the active coordinate of
![]() $F_{n+1}$
. We perform a recursion along the lexicographic order of the set
$F_{n+1}$
. We perform a recursion along the lexicographic order of the set
Note that its members correspond to functions
 $$ \begin{align}\sigma \in \prod\limits_{\beta\in F_{n+1}\cap \gamma } \, ^{\eta_{n+1}(\beta)+1}2\end{align} $$
$$ \begin{align}\sigma \in \prod\limits_{\beta\in F_{n+1}\cap \gamma } \, ^{\eta_{n+1}(\beta)+1}2\end{align} $$
which are then ordered accordingly, say by
![]() $\prec $
.
$\prec $
.
We have two subcases according to whether
![]() $n+1=\min (Z(\gamma ))$
or not. In the second case we shall apply
$n+1=\min (Z(\gamma ))$
or not. In the second case we shall apply
![]() $(\ast )_{m}$
for some
$(\ast )_{m}$
for some
![]() $m<n+1$
in
$m<n+1$
in
![]() $Z(\gamma )$
and perform the same recursion as will be done in the first case after some preliminary step. Hence we treat only the first case.
$Z(\gamma )$
and perform the same recursion as will be done in the first case after some preliminary step. Hence we treat only the first case.
In the first case, as for the construction of
![]() $p_0$
, (working in
$p_0$
, (working in
![]() $\mathbf {V}[ \dot {G}_\gamma ] $
) we first have to apply our assumption together with (G1) to extend
$\mathbf {V}[ \dot {G}_\gamma ] $
) we first have to apply our assumption together with (G1) to extend
![]() $p_n\upharpoonright [ \gamma ,\alpha )$
to some
$p_n\upharpoonright [ \gamma ,\alpha )$
to some
![]() $p^1\in P_\alpha /\dot {G}_\gamma $
such that
$p^1\in P_\alpha /\dot {G}_\gamma $
such that
![]() $p^1\leq _{F_{n+1}\setminus \gamma +1, \eta _{n+1}\upharpoonright F_{n+1}\setminus \gamma +1}p_n\upharpoonright [ \gamma ,\alpha )$
and
$p^1\leq _{F_{n+1}\setminus \gamma +1, \eta _{n+1}\upharpoonright F_{n+1}\setminus \gamma +1}p_n\upharpoonright [ \gamma ,\alpha )$
and
Such
![]() $p^1$
is obtained as the last element of a
$p^1$
is obtained as the last element of a
![]() $\leq _{F_{n+1}\setminus \gamma +1, \eta _{n+1}\upharpoonright F_{n+1}\setminus \gamma +1 }$
-decreasing chain considering each
$\leq _{F_{n+1}\setminus \gamma +1, \eta _{n+1}\upharpoonright F_{n+1}\setminus \gamma +1 }$
-decreasing chain considering each
 $$ \begin{align}\tau \in \prod\limits_{\beta\in F_{n+1}\setminus \gamma +1 } \, ^{\eta_{n+1}(\beta)+1}2.\end{align} $$
$$ \begin{align}\tau \in \prod\limits_{\beta\in F_{n+1}\setminus \gamma +1 } \, ^{\eta_{n+1}(\beta)+1}2.\end{align} $$
As pedantically,
![]() $p^1$
is a only name for a condition in the quotient forcing (hence
$p^1$
is a only name for a condition in the quotient forcing (hence
![]() $(p_n\upharpoonright \gamma , p^1)$
is not a member of
$(p_n\upharpoonright \gamma , p^1)$
is not a member of
![]() $P_\alpha $
), by properness we obtain
$P_\alpha $
), by properness we obtain
![]() $p^0\leq _{F_n\cap \gamma , \eta _n\upharpoonright \gamma } p_n\upharpoonright \gamma $
which decides supp
$p^0\leq _{F_n\cap \gamma , \eta _n\upharpoonright \gamma } p_n\upharpoonright \gamma $
which decides supp
![]() $(p^1)$
, i.e., turns
$(p^1)$
, i.e., turns
![]() $p^1$
into a countable sequence of names so that
$p^1$
into a countable sequence of names so that
![]() $(p^0,p^1)$
will be a member of
$(p^0,p^1)$
will be a member of
![]() $P_\alpha $
. (See [Reference Baumgartner and Mathias1, Section 5] for more details about this.)
$P_\alpha $
. (See [Reference Baumgartner and Mathias1, Section 5] for more details about this.)
Now we start our recursion below
![]() $(p^0,p^1)$
. Let
$(p^0,p^1)$
. Let
![]() $\sigma $
be the first sequence as in (3). We have to construct
$\sigma $
be the first sequence as in (3). We have to construct
![]() $q\leq _{F_n,\eta _n} (p^0,p^1) $
such that for every pair of
$q\leq _{F_n,\eta _n} (p^0,p^1) $
such that for every pair of
and every
![]() $\tau $
as in (5), if
$\tau $
as in (5), if
![]() $u_0\upharpoonright \eta _{n+1}(\gamma ) =u_1\upharpoonright \eta _{n+1}(\gamma )$
and
$u_0\upharpoonright \eta _{n+1}(\gamma ) =u_1\upharpoonright \eta _{n+1}(\gamma )$
and
![]() $u_0( \eta _{n+1}(\gamma ))<u_1 (\eta _{n+1}(\gamma ))$
then
$u_0( \eta _{n+1}(\gamma ))<u_1 (\eta _{n+1}(\gamma ))$
then
and, letting
denote the longest common initial segment of these two incompatible nodes, we have
for every
![]() $s\in \,^{n}2$
. Note that
$s\in \,^{n}2$
. Note that
![]() $t(q,\sigma , (u_0,u_1),\tau )=t_s$
for some
$t(q,\sigma , (u_0,u_1),\tau )=t_s$
for some
![]() $s\in \,^{n+1}2$
.
$s\in \,^{n+1}2$
.
This is easy to achieve. Simply build a finite
![]() $\leq _{F_n,\eta _n}$
-descending chain of conditions
$\leq _{F_n,\eta _n}$
-descending chain of conditions
![]() $r\leq (p^0,p^1)$
taking care of every
$r\leq (p^0,p^1)$
taking care of every
![]() $(u_0,u_1)$
and
$(u_0,u_1)$
and
![]() $\tau $
as above. More precisely, if we have obtained r and have to consider
$\tau $
as above. More precisely, if we have obtained r and have to consider
![]() $(u_0,u_1)$
and
$(u_0,u_1)$
and
![]() $\tau $
, by (4) we know
$\tau $
, by (4) we know
Choose
![]() $G_\gamma $
a
$G_\gamma $
a
![]() $P_\gamma $
-generic filter with
$P_\gamma $
-generic filter with
![]() $r\upharpoonright \gamma \ast \sigma \in G_\gamma $
. Work in
$r\upharpoonright \gamma \ast \sigma \in G_\gamma $
. Work in
![]() $\mathbf {V}\left [ G_\gamma \right ] $
. Let
$\mathbf {V}\left [ G_\gamma \right ] $
. Let
![]() $u:= u_0\upharpoonright \eta _{n+1}(\gamma ) = u_1\upharpoonright \eta _{n+1}(\gamma ) $
. Choose
$u:= u_0\upharpoonright \eta _{n+1}(\gamma ) = u_1\upharpoonright \eta _{n+1}(\gamma ) $
. Choose
![]() $r'\leq (r(\gamma )^{u}, r\upharpoonright [ \gamma +1,\alpha )\ast \tau )$
deciding an initial segment of
$r'\leq (r(\gamma )^{u}, r\upharpoonright [ \gamma +1,\alpha )\ast \tau )$
deciding an initial segment of
![]() $\dot x$
, say
$\dot x$
, say
![]() $\xi $
, that is longer than all the
$\xi $
, that is longer than all the
![]() $t_s$
for
$t_s$
for
![]() $s\in \,^{n}2$
, and let
$s\in \,^{n}2$
, and let
![]() $k=\min (\mathrm {com}(r'(\gamma )))$
. By (4) we can find
$k=\min (\mathrm {com}(r'(\gamma )))$
. By (4) we can find
![]() $r"\leq r' $
such that
$r"\leq r' $
such that
![]() $k\in \mathrm {com}(r"(\gamma ))$
and
$k\in \mathrm {com}(r"(\gamma ))$
and
Then let
![]() $r_1$
be such that
$r_1$
be such that
![]() $r_1(\gamma )$
is
$r_1(\gamma )$
is
![]() $r(\gamma )$
except that
$r(\gamma )$
except that
![]() $r_1(\gamma )^{u} =r"(\gamma )$
and
$r_1(\gamma )^{u} =r"(\gamma )$
and
Finally choose
![]() $r_0\leq _{F_n\cap \gamma , \eta _n} r\upharpoonright \gamma $
such that
$r_0\leq _{F_n\cap \gamma , \eta _n} r\upharpoonright \gamma $
such that
![]() $r_0\ast \sigma \in G_\gamma $
forces all this, decides
$r_0\ast \sigma \in G_\gamma $
forces all this, decides
![]() $\xi $
and also decides supp
$\xi $
and also decides supp
![]() $(r_1)$
(see the above remark how to get
$(r_1)$
(see the above remark how to get
![]() $(p^0,p^1)$
). Then
$(p^0,p^1)$
). Then
![]() $r=(r_0,r_1) $
is the next condition in our finite chain. Let q be its last element. We denote
$r=(r_0,r_1) $
is the next condition in our finite chain. Let q be its last element. We denote
![]() $q=(q\upharpoonright \gamma , q\upharpoonright \left [ \gamma ,\alpha \right )) $
by
$q=(q\upharpoonright \gamma , q\upharpoonright \left [ \gamma ,\alpha \right )) $
by
![]() $ (q_\sigma ,q^\sigma )$
.
$ (q_\sigma ,q^\sigma )$
.
Now suppose we have already dealt with an initial segment of
![]() $\sigma $
’s as in (3), built a
$\sigma $
’s as in (3), built a
![]() $\leq _{F_n,\eta _n}$
-descending chain of conditions below
$\leq _{F_n,\eta _n}$
-descending chain of conditions below
![]() $(p^0,p^1)$
with last element
$(p^0,p^1)$
with last element
![]() $q $
, and
$q $
, and
![]() $\sigma '$
is the next sequence we have to consider. We essentially repeat the above recursion below
$\sigma '$
is the next sequence we have to consider. We essentially repeat the above recursion below
![]() $q $
, but this time deciding long enough initial segments of
$q $
, but this time deciding long enough initial segments of
![]() $\dot x$
so that
$\dot x$
so that
will hold for every
![]() $\sigma \prec \sigma '$
and all
$\sigma \prec \sigma '$
and all
![]() $(u_0,u_1), (u_0',u_1'),\tau ,\tau '$
as above. Suppose now we have done this for every
$(u_0,u_1), (u_0',u_1'),\tau ,\tau '$
as above. Suppose now we have done this for every
![]() $\sigma $
. We define
$\sigma $
. We define
![]() $p_{n+1}$
as the last condition we have obtained. Then by construction we have
$p_{n+1}$
as the last condition we have obtained. Then by construction we have
for every
![]() $\sigma $
,
$\sigma $
,
![]() $(u_0,u_1)$
and
$(u_0,u_1)$
and
![]() $\tau $
, and if
$\tau $
, and if
![]() $\sigma \prec \sigma '$
then
$\sigma \prec \sigma '$
then
for any
![]() $(u_0,u_1),(u_0',u_1'),\tau ,\tau '$
. Hence the theorem is proved.
$(u_0,u_1),(u_0',u_1'),\tau ,\tau '$
. Hence the theorem is proved.
Remark 3.1. Suppose that
![]() $\dot x$
, the fusion sequence
$\dot x$
, the fusion sequence
![]() $\bar S=\langle (p_n,F_n,\eta _n): n<\omega \rangle $
and
$\bar S=\langle (p_n,F_n,\eta _n): n<\omega \rangle $
and
![]() $\langle t_s:s\in \, ^{<\omega }2\rangle $
are as in Theorem 3.1 and let
$\langle t_s:s\in \, ^{<\omega }2\rangle $
are as in Theorem 3.1 and let
![]() $p_\omega $
be the fusion limit of
$p_\omega $
be the fusion limit of
![]() $\bar S$
. Moreover, associated with these we have the refining finite antichains
$\bar S$
. Moreover, associated with these we have the refining finite antichains
![]() $A_n(\bar {S})=\langle a^s:s\in \,^n2\rangle $
as explained in Remark 2.1(3).
$A_n(\bar {S})=\langle a^s:s\in \,^n2\rangle $
as explained in Remark 2.1(3).
(1) Let
![]() $T=T(\dot x, \bar S)$
be the tree generated by
$T=T(\dot x, \bar S)$
be the tree generated by
![]() $\bar {t}=\langle t_s:s\in \, ^n2\rangle $
. By construction,
$\bar {t}=\langle t_s:s\in \, ^n2\rangle $
. By construction,
![]() $T\subseteq \, ^{<\omega }\omega $
is a
$T\subseteq \, ^{<\omega }\omega $
is a
![]() $2$
-ary tree such that
$2$
-ary tree such that
and
![]() ${\mathrm {split}}(T)= \left \lbrace t_s: s\in \, ^{<\omega }2\right \rbrace $
. Moreover
${\mathrm {split}}(T)= \left \lbrace t_s: s\in \, ^{<\omega }2\right \rbrace $
. Moreover
is the tree of possibilities for
![]() $\dot {x}$
below
$\dot {x}$
below
![]() $p_\omega $
.
$p_\omega $
.
(2) If we step into
![]() $\mathbf {V}[G_\gamma ]$
for some
$\mathbf {V}[G_\gamma ]$
for some
![]() $\gamma <\omega _2$
, where
$\gamma <\omega _2$
, where
![]() $G_\gamma $
is
$G_\gamma $
is
![]() $P_\gamma $
-generic containing
$P_\gamma $
-generic containing
![]() $p_\omega \upharpoonright \gamma $
, then
$p_\omega \upharpoonright \gamma $
, then
![]() $G_\gamma $
evaluates
$G_\gamma $
evaluates
![]() $\dot {x}$
partially. More precisely, the generic reals
$\dot {x}$
partially. More precisely, the generic reals
![]() $\langle g_\beta :\beta \in \mathrm {supp}( {p_\omega })\cap \gamma \rangle $
determine a possibly partial function
$\langle g_\beta :\beta \in \mathrm {supp}( {p_\omega })\cap \gamma \rangle $
determine a possibly partial function
![]() $H_\gamma =H_\gamma (\bar {S}):\omega \rightarrow 2$
with
$H_\gamma =H_\gamma (\bar {S}):\omega \rightarrow 2$
with
such that for every
![]() $n<\omega $
, only those
$n<\omega $
, only those
![]() $a^s(\bar {S})$
in
$a^s(\bar {S})$
in
![]() $A_n(\bar {S})$
are compatible with
$A_n(\bar {S})$
are compatible with
![]() $p_\omega \left [ G_\gamma \right ] $
for which s is compatible with
$p_\omega \left [ G_\gamma \right ] $
for which s is compatible with
![]() $H_\gamma $
, and hence
$H_\gamma $
, and hence
is a maximal antichain in the quotient forcing
![]() $P_{\omega _2}/G_\gamma $
below
$P_{\omega _2}/G_\gamma $
below
![]() $p_\omega \left [ G_\gamma \right ] $
. More explicitly, given
$p_\omega \left [ G_\gamma \right ] $
. More explicitly, given
![]() $\beta \in \mathrm {supp}(p_\omega )\cap \gamma $
and
$\beta \in \mathrm {supp}(p_\omega )\cap \gamma $
and
![]() $i\in Z(\beta )$
, we have
$i\in Z(\beta )$
, we have
(See Definition 2.2(6).)
Note that for any
![]() $a^s(\bar {S})\left [ G_\gamma \right ] , a^{s'}(\bar {S})\left [ G_\gamma \right ] \in A^\gamma _n(\bar {S})\left [ G_\gamma \right ]$
we have
$a^s(\bar {S})\left [ G_\gamma \right ] , a^{s'}(\bar {S})\left [ G_\gamma \right ] \in A^\gamma _n(\bar {S})\left [ G_\gamma \right ]$
we have
Clearly,
![]() $H_\gamma $
is a total function iff
$H_\gamma $
is a total function iff
![]() $\mathrm {supp}( {p_\omega })\subseteq \gamma $
, otherwise
$\mathrm {supp}( {p_\omega })\subseteq \gamma $
, otherwise
![]() $H_\gamma $
is a Silver function, and if
$H_\gamma $
is a Silver function, and if
![]() $\beta <\gamma $
,
$\beta <\gamma $
,
![]() $H_\gamma \upharpoonright Z(\beta )$
is completely determined by
$H_\gamma \upharpoonright Z(\beta )$
is completely determined by
![]() $g_\beta $
, hence belongs to
$g_\beta $
, hence belongs to
![]() $\mathbf {V}^{P_{\beta +1 }}$
.
$\mathbf {V}^{P_{\beta +1 }}$
.
Corollary 3.1 [Reference Rosłanowski and Steprāns9, Corollary 2.6].
The CS-iteration of
![]() $\mathbb {SI}$
has the 2-localization property.
$\mathbb {SI}$
has the 2-localization property.
As outlined in the introduction, [Reference Rosłanowski and Steprāns9, Corollary 2.6] proves the k-localization property for the CS-iteration of
![]() $\mathbb {SI}_k$
, as well as for
$\mathbb {SI}_k$
, as well as for
![]() $\mathbb {U}_k$
and k-dimensional Sacks forcing
$\mathbb {U}_k$
and k-dimensional Sacks forcing
![]() $\mathbb {S}_k$
, for every
$\mathbb {S}_k$
, for every
![]() $2\leq k<\omega $
.
$2\leq k<\omega $
.
4
 $\mathfrak {C}_2$
-sets covering new reals
$\mathfrak {C}_2$
-sets covering new reals
In this section we prove that, given any
![]() $P_{\omega _2}$
-name
$P_{\omega _2}$
-name
![]() $\dot x$
for a new real, where
$\dot x$
for a new real, where
![]() $P_{\omega _2}$
is the CS-iteration of
$P_{\omega _2}$
is the CS-iteration of
![]() $\mathbb {SI}$
, it is possible to define a coding system
$\mathbb {SI}$
, it is possible to define a coding system
![]() $\langle u^b:b\in \Omega \rangle $
in the ground model such that
$\langle u^b:b\in \Omega \rangle $
in the ground model such that
![]() $\Vdash _{P_{\omega _2}}\; \forall b\in \Omega \quad \dot x\not \in [ u^b ] .$
Let me first explain the core idea in the simple case where we replace
$\Vdash _{P_{\omega _2}}\; \forall b\in \Omega \quad \dot x\not \in [ u^b ] .$
Let me first explain the core idea in the simple case where we replace
![]() ${P_{\omega _2}}$
by
${P_{\omega _2}}$
by
![]() $\mathbb {SI}$
and
$\mathbb {SI}$
and
![]() $\dot x$
by the
$\dot x$
by the
![]() $\mathbb {SI}$
-name
$\mathbb {SI}$
-name
![]() $\dot g$
for the Silver real.
$\dot g$
for the Silver real.
From now on let
![]() $\Omega $
denote the set of all infinite and coinfinite subsets of
$\Omega $
denote the set of all infinite and coinfinite subsets of
![]() $\omega $
. For
$\omega $
. For
![]() $b\in \Omega $
we define
$b\in \Omega $
we define
![]() $u^b\in \mathbb {U}$
with
$u^b\in \mathbb {U}$
with
![]() $a^{u^b}=\omega \setminus b$
(see Definition 2.1(2)) by recursion on levels as follows: Suppose we have
$a^{u^b}=\omega \setminus b$
(see Definition 2.1(2)) by recursion on levels as follows: Suppose we have
![]() $n\in b$
and
$n\in b$
and
![]() $t\in u^b\cap \,^n2$
. For any finite partial function s from
$t\in u^b\cap \,^n2$
. For any finite partial function s from
![]() $\omega $
to
$\omega $
to
![]() $2$
we let
$2$
we let
We stipulate that
![]() $t\,^\smallfrown \, i_t$
is the (only) successor node of t in
$t\,^\smallfrown \, i_t$
is the (only) successor node of t in
![]() $u^b$
. Hence
$u^b$
. Hence
![]() $u^b$
is defined and thus also the coding system
$u^b$
is defined and thus also the coding system
![]() $C=\langle u^b: b\in \Omega \rangle $
. Now we can prove:
$C=\langle u^b: b\in \Omega \rangle $
. Now we can prove:
Recall
For this, let
![]() $f\in \mathbb {SI}$
and
$f\in \mathbb {SI}$
and
![]() $b\in \Omega $
. Let
$b\in \Omega $
. Let
![]() $m=\min (\mathrm {com}(f))$
and
$m=\min (\mathrm {com}(f))$
and
![]() $n=\min (b\setminus m+1)$
. Wlog we may assume that
$n=\min (b\setminus m+1)$
. Wlog we may assume that
![]() $n+1\setminus \left \lbrace m\right \rbrace \subseteq \;\mathrm {dom}(f)$
. Define
$n+1\setminus \left \lbrace m\right \rbrace \subseteq \;\mathrm {dom}(f)$
. Define
 $$\begin{align*}k = \left\{\begin{array}{cl} 0, & {\mathrm{if}}\; i_{f\upharpoonright n\setminus\left\lbrace m\right\rbrace }=1-f(n)\\ 1, & {\mathrm{otherwise}} \end{array} \right.\end{align*}$$
$$\begin{align*}k = \left\{\begin{array}{cl} 0, & {\mathrm{if}}\; i_{f\upharpoonright n\setminus\left\lbrace m\right\rbrace }=1-f(n)\\ 1, & {\mathrm{otherwise}} \end{array} \right.\end{align*}$$
and
![]() $f'=f\cup \left \lbrace (m,k)\right \rbrace $
. Then clearly
$f'=f\cup \left \lbrace (m,k)\right \rbrace $
. Then clearly
![]() $f'\Vdash _{\mathbb {SI}}\;\dot g\not \in \left [ u^b\right ] $
, as
$f'\Vdash _{\mathbb {SI}}\;\dot g\not \in \left [ u^b\right ] $
, as
![]() $f'\upharpoonright n+1\not \in u^b$
. This proves
$f'\upharpoonright n+1\not \in u^b$
. This proves
![]() $(\ast )$
. In the general case, the correct definition of C is more complex. It is given in the following definition. Then Lemma 4.1 will generalize the above argument.
$(\ast )$
. In the general case, the correct definition of C is more complex. It is given in the following definition. Then Lemma 4.1 will generalize the above argument.
Definition 4.1. (1) Let Y be a nonempty set of ordinals and
![]() $\bar {Z} =\langle Z(\beta ): \beta \in Y \rangle $
a partition of
$\bar {Z} =\langle Z(\beta ): \beta \in Y \rangle $
a partition of
![]() $\omega $
into infinite sets. Let
$\omega $
into infinite sets. Let
Let
![]() $T\subseteq \,^{<\omega }2$
be a perfect tree such that
$T\subseteq \,^{<\omega }2$
be a perfect tree such that
![]() $\bar {t}=\langle t_s:s\in \, ^{<\omega }2\rangle $
enumerates canonically
$\bar {t}=\langle t_s:s\in \, ^{<\omega }2\rangle $
enumerates canonically
![]() $\mathrm {split}(T)$
, hence
$\mathrm {split}(T)$
, hence
![]() $\left \lbrace t_s: s\in \, ^n2\right \rbrace =\mathrm {split}_n(T)$
, such that the following are satisfied:
$\left \lbrace t_s: s\in \, ^n2\right \rbrace =\mathrm {split}_n(T)$
, such that the following are satisfied:
-
(i)
 $\vert t_s\vert <\vert t_{s'}\vert $
whenever
$\vert t_s\vert <\vert t_{s'}\vert $
whenever
 $\vert s\vert <\vert s'\vert $
;
$\vert s\vert <\vert s'\vert $
; -
(ii) if
 $n\in Z(\gamma )$
and
$n\in Z(\gamma )$
and
 $s, s'\in \, ^{n}2 $
are such that we have
$s, s'\in \, ^{n}2 $
are such that we have $$ \begin{align*}s\upharpoonright n\setminus \bigcup \left\lbrace Z(\beta):\beta\geq \gamma\right\rbrace\ne s'\upharpoonright n\setminus \bigcup \left\lbrace Z(\beta):\beta\geq \gamma\right\rbrace\!,\end{align*} $$
$$ \begin{align*}s\upharpoonright n\setminus \bigcup \left\lbrace Z(\beta):\beta\geq \gamma\right\rbrace\ne s'\upharpoonright n\setminus \bigcup \left\lbrace Z(\beta):\beta\geq \gamma\right\rbrace\!,\end{align*} $$
 $\vert t_s\vert \ne \vert t_{s'}\vert $
.
$\vert t_s\vert \ne \vert t_{s'}\vert $
.
Such a tree
![]() $T $
will be called a coding tree and we write
$T $
will be called a coding tree and we write
![]() $T= T(\bar Z)$
to indicate with respect to which
$T= T(\bar Z)$
to indicate with respect to which
![]() $\bar Z$
property (ii) is satisfied.
$\bar Z$
property (ii) is satisfied.
Given such T we define a coding system
![]() $C=C(T)=\langle u^b:b\in \Omega (T)\rangle $
as follows: For
$C=C(T)=\langle u^b:b\in \Omega (T)\rangle $
as follows: For
![]() $\beta \in Y$
let
$\beta \in Y$
let
Clearly, by (i) the
![]() $L(\beta )$
are infinite and pairwise disjoint. We define
$L(\beta )$
are infinite and pairwise disjoint. We define
![]() $\Omega (T )$
as follows:
$\Omega (T )$
as follows:
![]() $\Omega (T)= \Omega \cap \lbrace b : \left [ \exists \beta \in Y\,\, b\subseteq L(\beta ) \right ] \,\vee \, [ b\subseteq \bigcup \limits _{\beta \in Y} L(\beta ) \;\wedge $
$\Omega (T)= \Omega \cap \lbrace b : \left [ \exists \beta \in Y\,\, b\subseteq L(\beta ) \right ] \,\vee \, [ b\subseteq \bigcup \limits _{\beta \in Y} L(\beta ) \;\wedge $
![]() $\qquad \qquad \qquad \qquad \qquad \forall \beta \in Y\,\, \vert b\cap L(\beta ))\vert \leq 1 ] \,\vee \, [ b\cap \bigcup \limits _{\beta \in Y} L(\beta ) =\emptyset ] \rbrace .$
$\qquad \qquad \qquad \qquad \qquad \forall \beta \in Y\,\, \vert b\cap L(\beta ))\vert \leq 1 ] \,\vee \, [ b\cap \bigcup \limits _{\beta \in Y} L(\beta ) =\emptyset ] \rbrace .$
Clearly
![]() $\Omega (T)$
is dense in
$\Omega (T)$
is dense in
![]() $\left [ \omega \right ] ^{\omega }$
and every
$\left [ \omega \right ] ^{\omega }$
and every
![]() $b\in \Omega (T)$
is coinfinite.
$b\in \Omega (T)$
is coinfinite.
We define
![]() $C= \langle u^b:b\in \Omega (T)\rangle $
such that for
$C= \langle u^b:b\in \Omega (T)\rangle $
such that for
![]() $b\in \Omega (T)$
we have
$b\in \Omega (T)$
we have
![]() $u^b\in \mathbb {U}$
with
$u^b\in \mathbb {U}$
with
![]() $a^{u^b}=\omega \setminus b$
defined according to the three types of members of
$a^{u^b}=\omega \setminus b$
defined according to the three types of members of
![]() $\Omega (T)$
as follows:
$\Omega (T)$
as follows:
-
(I) Suppose
 $b\subseteq L(\beta )$
for
$b\subseteq L(\beta )$
for
 $\beta \in Y$
. We determine whether
$\beta \in Y$
. We determine whether
 $t\in \, ^{n+1}2$
belongs to
$t\in \, ^{n+1}2$
belongs to
 $u^b$
by recursion on
$u^b$
by recursion on
 $n\in b$
. Suppose
$n\in b$
. Suppose
 $t\in u^b\cap \, ^n2$
. Now we require the following:
$t\in u^b\cap \, ^n2$
. Now we require the following:-
• if
 $t\not \in T$
let
$t\not \in T$
let
 $t\,^\smallfrown \, 0\in u^b$
;
$t\,^\smallfrown \, 0\in u^b$
; -
• if
 $t \in T\setminus \mathrm {split}(T)$
let
$t \in T\setminus \mathrm {split}(T)$
let
 $t\,^\smallfrown \, i\in u^b$
such that
$t\,^\smallfrown \, i\in u^b$
such that
 $t\,^\smallfrown \, i\not \in T$
;
$t\,^\smallfrown \, i\not \in T$
; -
• if
 $t\in \mathrm {split}(T)$
, thus
$t\in \mathrm {split}(T)$
, thus
 $t=t_s$
for some
$t=t_s$
for some
 $s\in \,^{<\omega }2$
, letting we stipulate that
$s\in \,^{<\omega }2$
, letting we stipulate that $$ \begin{align*}i(t,\beta):= \vert \left\lbrace j\in \vert s\vert \cap Z(\beta) :s(j)=1\right\rbrace \vert \,\mathrm{mod}\,2,\end{align*} $$
$$ \begin{align*}i(t,\beta):= \vert \left\lbrace j\in \vert s\vert \cap Z(\beta) :s(j)=1\right\rbrace \vert \,\mathrm{mod}\,2,\end{align*} $$
 $$ \begin{align*}t\,^\smallfrown\, t_{s\,^\smallfrown\, i(t,\beta)}(\vert t\vert )\in u^b.\end{align*} $$
$$ \begin{align*}t\,^\smallfrown\, t_{s\,^\smallfrown\, i(t,\beta)}(\vert t\vert )\in u^b.\end{align*} $$
-
-
(II) Suppose
 $\forall \beta \in Y\; \vert b\cap L(\beta )\vert \leq 1$
and
$\forall \beta \in Y\; \vert b\cap L(\beta )\vert \leq 1$
and
 $b\subseteq \bigcup \limits _{\beta \in Y} L(\beta ) $
. We require the following:
$b\subseteq \bigcup \limits _{\beta \in Y} L(\beta ) $
. We require the following:-
• if
 $t\not \in T$
or
$t\not \in T$
or
 $t\in \mathrm {split}(T)$
let
$t\in \mathrm {split}(T)$
let
 $t\,^\smallfrown \, 0\in u^b$
;
$t\,^\smallfrown \, 0\in u^b$
; -
• if
 $t \in T\setminus \mathrm {split}(T)$
let
$t \in T\setminus \mathrm {split}(T)$
let
 $t\,^\smallfrown \, i\in u^b$
such that
$t\,^\smallfrown \, i\in u^b$
such that
 $t\,^\smallfrown \, i\not \in T$
;
$t\,^\smallfrown \, i\not \in T$
;
-
-
(III) Suppose
 $ b\cap \bigcup \limits _{\beta \in Y} L(\beta ) =\emptyset $
. Hence for no
$ b\cap \bigcup \limits _{\beta \in Y} L(\beta ) =\emptyset $
. Hence for no
 $t\in \,\mathrm {split}(T)$
do we have
$t\in \,\mathrm {split}(T)$
do we have
 $\vert t\vert \in b$
. We define
$\vert t\vert \in b$
. We define
 $u^b$
as in case II.
$u^b$
as in case II.
(2) Suppose that the objects as in (1) are given and
![]() $Y'$
is another countable set of ordinals that is order isomorphic to Y. Let
$Y'$
is another countable set of ordinals that is order isomorphic to Y. Let
![]() $\pi :Y\rightarrow Y'$
be the isomorphism. Let
$\pi :Y\rightarrow Y'$
be the isomorphism. Let
![]() $\bar Z'=\langle Z'(\beta ):\beta \in Y'\rangle $
be the partition of
$\bar Z'=\langle Z'(\beta ):\beta \in Y'\rangle $
be the partition of
![]() $\omega $
induced by
$\omega $
induced by
![]() $\pi $
, i.e.,
$\pi $
, i.e.,
![]() $Z'(\pi (\beta ))=Z(\beta )$
for every
$Z'(\pi (\beta ))=Z(\beta )$
for every
![]() $\beta \in Y$
. Similarly, we obtain the induced finite sets
$\beta \in Y$
. Similarly, we obtain the induced finite sets
![]() $F_n'\subseteq Y'$
such that
$F_n'\subseteq Y'$
such that
![]() $Y'=\bigcup \left \lbrace F_n':n<\omega \right \rbrace \!.$
$Y'=\bigcup \left \lbrace F_n':n<\omega \right \rbrace \!.$
Then clearly (1)(ii) holds for
![]() $F_n', Z'(\beta )$
as well and
$F_n', Z'(\beta )$
as well and
![]() $L(\beta )=L'(\pi (\beta ))$
, where
$L(\beta )=L'(\pi (\beta ))$
, where
Moreover,
![]() $\Omega (T(\bar Z))=\Omega (T(\bar Z'))$
and we obtain the same trees
$\Omega (T(\bar Z))=\Omega (T(\bar Z'))$
and we obtain the same trees
![]() $u^b$
if we replace
$u^b$
if we replace
![]() $Z(\beta )$
by
$Z(\beta )$
by
![]() $Z'(\pi (\beta ))$
and
$Z'(\pi (\beta ))$
and
![]() $L(\beta )$
by
$L(\beta )$
by
![]() $L'(\pi (\beta ))$
.
$L'(\pi (\beta ))$
.
Lemma 4.1. Suppose that
![]() $P_\alpha $
is a CS-iteration of
$P_\alpha $
is a CS-iteration of
![]() $\mathbb {SI}$
,
$\mathbb {SI}$
,
![]() $p\in P_\alpha $
and
$p\in P_\alpha $
and
Suppose also that
![]() $\bar S=\langle (p_n,F_n,\eta _n):n<\omega \rangle $
is a fusion sequence below p with limit
$\bar S=\langle (p_n,F_n,\eta _n):n<\omega \rangle $
is a fusion sequence below p with limit
![]() $p_\omega $
for
$p_\omega $
for
![]() $\dot x$
as in Theorem 3.1. Hence we have the associated partition
$\dot x$
as in Theorem 3.1. Hence we have the associated partition
![]() $\bar {Z}=\langle Z(\beta ):\beta \in \,\mathrm {supp}(p_\omega )\rangle $
and perfect tree
$\bar {Z}=\langle Z(\beta ):\beta \in \,\mathrm {supp}(p_\omega )\rangle $
and perfect tree
![]() $T=T(\dot x, \bar S)$
with splitnodes
$T=T(\dot x, \bar S)$
with splitnodes
![]() $\bar t =\langle t_s: s\in \, ^n2\rangle $
. Clearly
$\bar t =\langle t_s: s\in \, ^n2\rangle $
. Clearly
![]() $T=T(\bar Z)$
is a coding tree as in Definition 4.1. If the coding system
$T=T(\bar Z)$
is a coding tree as in Definition 4.1. If the coding system
![]() $C=C(T )= \langle u^b:b\in \Omega (T)\rangle $
is defined as there we have
$C=C(T )= \langle u^b:b\in \Omega (T)\rangle $
is defined as there we have
Proof. Suppose that
![]() $q\leq p_\omega $
and
$q\leq p_\omega $
and
![]() $b\in \Omega (T)\cap \mathbf {V}$
are arbitrary. We have to find
$b\in \Omega (T)\cap \mathbf {V}$
are arbitrary. We have to find
![]() $q'\leq q$
such that
$q'\leq q$
such that
Let the antichains
![]() $A_n(\bar {S})=\langle a^s: s\in \,^{n}2\rangle $
be defined as in Remark 2.1(3).
$A_n(\bar {S})=\langle a^s: s\in \,^{n}2\rangle $
be defined as in Remark 2.1(3).
Define
and let
be the tree of possibilities for
![]() $\dot {x}$
below q. Clearly,
$\dot {x}$
below q. Clearly,
![]() $R^q$
and
$R^q$
and
![]() $T^q$
are trees and
$T^q$
are trees and
![]() $T^q$
is generated by
$T^q$
is generated by
![]() $ \left \lbrace t_s: s \in R^q \right \rbrace \!.$
Also note that if
$ \left \lbrace t_s: s \in R^q \right \rbrace \!.$
Also note that if
![]() $t\in T^q$
and
$t\in T^q$
and
![]() $t=t_s$
for some s, then
$t=t_s$
for some s, then
![]() $s\in R^q$
, as otherwise let
$s\in R^q$
, as otherwise let
![]() $s_0\in R^q$
be maximal with
$s_0\in R^q$
be maximal with
![]() $s_0\subseteq s$
. Hence every
$s_0\subseteq s$
. Hence every
![]() $s'\in R^q$
that is not an initial segment of
$s'\in R^q$
that is not an initial segment of
![]() $s_0$
either extends
$s_0$
either extends
![]() $s_0\,^\smallfrown \, 1-s(\vert s_0\vert )$
or is incompatible with
$s_0\,^\smallfrown \, 1-s(\vert s_0\vert )$
or is incompatible with
![]() $s_0$
. As the
$s_0$
. As the
![]() $t_{s'}$
for
$t_{s'}$
for
![]() $s'\in \,^{<\omega }2$
are the splitnodes of T we conclude that
$s'\in \,^{<\omega }2$
are the splitnodes of T we conclude that
![]() $t\not \in T^q$
, a contradiction.
$t\not \in T^q$
, a contradiction.
Note that wlog we may assume that for every
![]() $l\in b$
and for every
$l\in b$
and for every
![]() $t\in T^q$
of length l there is
$t\in T^q$
of length l there is
![]() $s\in R^q$
such that
$s\in R^q$
such that
![]() $t=t_s$
. Indeed, otherwise we know by the remark we just made that t is not a splitnode of T but there is
$t=t_s$
. Indeed, otherwise we know by the remark we just made that t is not a splitnode of T but there is
![]() $q'\leq q$
forcing
$q'\leq q$
forcing
![]() $\dot {x}\upharpoonright l =t$
and hence by definition of
$\dot {x}\upharpoonright l =t$
and hence by definition of
![]() $u^b$
we have
$u^b$
we have
and we are done.
Now the proof proceeds along the three cases of Definition 4.1.
Case I:
We consider
![]() $b\subseteq L(\beta )$
for some
$b\subseteq L(\beta )$
for some
![]() $\beta \in \,\mathrm {supp}(p_\omega )$
.
$\beta \in \,\mathrm {supp}(p_\omega )$
.
Choose
![]() $G_\beta $
a
$G_\beta $
a
![]() $P_\beta $
-generic filter containing
$P_\beta $
-generic filter containing
![]() $q\upharpoonright \beta $
. Hence
$q\upharpoonright \beta $
. Hence
![]() $q(\beta )\left [ G_\beta \right ] \leq ^{\mathbb {SI}}p_\omega (\beta )\left [ G_\beta \right ]$
and there exist k and
$q(\beta )\left [ G_\beta \right ] \leq ^{\mathbb {SI}}p_\omega (\beta )\left [ G_\beta \right ]$
and there exist k and
![]() $v\in \,^{k}2$
such that
$v\in \,^{k}2$
such that
Let
![]() $m_0=\, \vert \mathrm {stem}(q(\beta )\left [ G_\beta \right ] )\vert $
. By the bookkeeping we used for the fusion by which we obtained
$m_0=\, \vert \mathrm {stem}(q(\beta )\left [ G_\beta \right ] )\vert $
. By the bookkeeping we used for the fusion by which we obtained
![]() $p_\omega $
we know the step at which coordinate
$p_\omega $
we know the step at which coordinate
![]() $\beta $
was active for the kth time, say it was step
$\beta $
was active for the kth time, say it was step
![]() $n_0$
. We choose
$n_0$
. We choose
![]() $l\in b$
larger than
$l\in b$
larger than
![]() $\max \lbrace \vert t_s\vert : s\in \,^{n_0}2\rbrace $
. By property (i) of a coding tree (see Definition 4.1) and by our observation above (that every
$\max \lbrace \vert t_s\vert : s\in \,^{n_0}2\rbrace $
. By property (i) of a coding tree (see Definition 4.1) and by our observation above (that every
![]() $t\in T^q$
of length l is of the form
$t\in T^q$
of length l is of the form
![]() $t_s$
for some
$t_s$
for some
![]() $s\in R^q$
), there is a unique
$s\in R^q$
), there is a unique
![]() $n_1\in Z(\beta )$
such that for every
$n_1\in Z(\beta )$
such that for every
![]() $t\in T^q$
of length l there exists
$t\in T^q$
of length l there exists
![]() $s\in \,^{n_1}2$
with
$s\in \,^{n_1}2$
with
![]() $t= t_s $
.
$t= t_s $
.
Moreover, in
![]() $\mathbf {V}[G_\beta ]$
the tree of possibilities for
$\mathbf {V}[G_\beta ]$
the tree of possibilities for
![]() $\dot {x}$
below q (with respect to the forcing
$\dot {x}$
below q (with respect to the forcing
![]() $P_{\alpha }/G_\beta $
) has been further restricted to
$P_{\alpha }/G_\beta $
) has been further restricted to
![]() $T^q[G_\beta ]$
defined as follows: Letting
$T^q[G_\beta ]$
defined as follows: Letting
![]() $T^q[G_\beta ]$
is the tree generated by the set of all
$T^q[G_\beta ]$
is the tree generated by the set of all
![]() $t_s$
with
$t_s$
with
![]() $s\in R^q[G_\beta ]$
.
$s\in R^q[G_\beta ]$
.
Given
![]() $s\in R^q[G_\beta ]\cap \,^{n_1}2$
and letting
$s\in R^q[G_\beta ]\cap \,^{n_1}2$
and letting
![]() $m_1= \dot {c}(p_\omega ,\beta )[G_\beta ](n_1)$
(see Definition 2.2(6)), the value of
$m_1= \dot {c}(p_\omega ,\beta )[G_\beta ](n_1)$
(see Definition 2.2(6)), the value of
![]() $\dot {x}(\vert t_s\vert )$
is determined by
$\dot {x}(\vert t_s\vert )$
is determined by
![]() $\dot {g}_\beta $
as
$\dot {g}_\beta $
as
![]() $t_{s\,^ \smallfrown \, \dot {g}_\beta (m_1)}( \vert t_s\vert ),$
more precisely, we have
$t_{s\,^ \smallfrown \, \dot {g}_\beta (m_1)}( \vert t_s\vert ),$
more precisely, we have
In
![]() $\mathbf {V}$
, we can find
$\mathbf {V}$
, we can find
![]() $\hat {q}\leq q $
in
$\hat {q}\leq q $
in
![]() $P_{\alpha }$
as follows:
$P_{\alpha }$
as follows:
![]() $\hat q\upharpoonright \beta \leq q\upharpoonright \beta $
forces all the facts we have noticed above after we fixed
$\hat q\upharpoonright \beta \leq q\upharpoonright \beta $
forces all the facts we have noticed above after we fixed
![]() $G_\beta $
, and
$G_\beta $
, and
![]() $\hat q\upharpoonright \beta $
also decides
$\hat q\upharpoonright \beta $
also decides
![]() $k,v,m_0,n_0,l, n_1,m_1$
as above. Moreover,
$k,v,m_0,n_0,l, n_1,m_1$
as above. Moreover,
![]() $\hat q\upharpoonright \beta $
decides
$\hat q\upharpoonright \beta $
decides
![]() $\hat {q}(\beta )\upharpoonright m_1+1$
, thus
$\hat {q}(\beta )\upharpoonright m_1+1$
, thus
![]() $\dot g_\beta \upharpoonright (m_1+1 \setminus \lbrace m_0\rbrace ) $
, say as
$\dot g_\beta \upharpoonright (m_1+1 \setminus \lbrace m_0\rbrace ) $
, say as
![]() $\langle g(0),...,g(m_0 -1),g(m_0 +1),...,g(m_1)\rangle $
, and we let
$\langle g(0),...,g(m_0 -1),g(m_0 +1),...,g(m_1)\rangle $
, and we let
![]() $\hat {q}\upharpoonright [\beta +1,\omega _2)=q\upharpoonright [\beta +1,\omega _2)$
.
$\hat {q}\upharpoonright [\beta +1,\omega _2)=q\upharpoonright [\beta +1,\omega _2)$
.
Now we can find
![]() $s_0,s_1\in R^{\hat {q}}\cap \, ^{n_1} 2$
such that
$s_0,s_1\in R^{\hat {q}}\cap \, ^{n_1} 2$
such that
![]() $s_i(n_0)=i$
and
$s_i(n_0)=i$
and
![]() $s_0(j) =s_1(j)$
for every
$s_0(j) =s_1(j)$
for every
![]() $j\in Z(\beta )\cap n_1\setminus \left \lbrace n_0\right \rbrace $
, and hence
$j\in Z(\beta )\cap n_1\setminus \left \lbrace n_0\right \rbrace $
, and hence
As remarked above, we know that both
![]() $t_{s_0}$
and
$t_{s_0}$
and
![]() $t_{s_1}$
are splitnodes of T of length l. Now choose j such that
$t_{s_1}$
are splitnodes of T of length l. Now choose j such that
![]() $i(t_{s_j\,^\smallfrown \,g(m_1)},\beta ) \ne g(m_1)$
and a common extension
$i(t_{s_j\,^\smallfrown \,g(m_1)},\beta ) \ne g(m_1)$
and a common extension
![]() $q'$
of
$q'$
of
![]() $\hat {q}$
and
$\hat {q}$
and
![]() $a^{s_j}$
. We conclude
$a^{s_j}$
. We conclude
and hence
![]() $q'\Vdash _{P_\alpha }\; \dot x\not \in \left [ u^b\right ],$
by definition of
$q'\Vdash _{P_\alpha }\; \dot x\not \in \left [ u^b\right ],$
by definition of
![]() $u^b$
.
$u^b$
.
Case II:
We have
![]() $b\subseteq \bigcup \limits _{\beta \in \mathrm {supp} (p_\omega )} L(\beta ) $
and
$b\subseteq \bigcup \limits _{\beta \in \mathrm {supp} (p_\omega )} L(\beta ) $
and
![]() $\forall \beta \in \,\mathrm {supp}(p_\omega )\; \vert b\cap L(\beta )\vert \leq 1$
. In this case we shall apply property (ii) of a coding tree (see Definition 4.1). As
$\forall \beta \in \,\mathrm {supp}(p_\omega )\; \vert b\cap L(\beta )\vert \leq 1$
. In this case we shall apply property (ii) of a coding tree (see Definition 4.1). As
is infinite (see Definition 2.2(6)), certainly we can find a large enough
![]() $\beta \in \,\mathrm {supp}(p_\omega )$
such that there are
$\beta \in \,\mathrm {supp}(p_\omega )$
such that there are
![]() $l\in b\cap L(\beta )$
,
$l\in b\cap L(\beta )$
,
![]() $n\in Z(\beta )$
and
$n\in Z(\beta )$
and
![]() $s\in \, ^{n}2$
,
$s\in \, ^{n}2$
,
![]() $ s_0,s_1\in \, ^{n}2\cap R^q$
such that
$ s_0,s_1\in \, ^{n}2\cap R^q$
such that
![]() $\vert t_s\vert =l$
and
$\vert t_s\vert =l$
and
By property (ii) of a coding tree we know that
![]() $\vert t_{s_0}\vert \ne \vert t_{s_1}\vert $
. Hence we can pick
$\vert t_{s_0}\vert \ne \vert t_{s_1}\vert $
. Hence we can pick
![]() $i<2$
such that
$i<2$
such that
![]() $\vert t_{s_i} \vert \ne l$
. We can find
$\vert t_{s_i} \vert \ne l$
. We can find
![]() $q'$
extending both q and
$q'$
extending both q and
![]() $a_{s_i}$
which decides
$a_{s_i}$
which decides
![]() $\dot x\upharpoonright l$
, say as t. By property (i) of a coding tree we know that t is not a splitting node of T, and hence
$\dot x\upharpoonright l$
, say as t. By property (i) of a coding tree we know that t is not a splitting node of T, and hence
by definition of
![]() $u^b$
.
$u^b$
.
Case III:
We have
![]() $b\cap \bigcup \limits _{\beta \in \mathrm {supp}(p_\omega )} L(\beta ) =\emptyset $
and we know that no
$b\cap \bigcup \limits _{\beta \in \mathrm {supp}(p_\omega )} L(\beta ) =\emptyset $
and we know that no
![]() $t\in \,\mathrm {split}(T)$
has
$t\in \,\mathrm {split}(T)$
has
![]() $\vert t\vert \in b$
. Hence by definition of
$\vert t\vert \in b$
. Hence by definition of
![]() $u^b$
we conclude
$u^b$
we conclude
Definition 4.2. Suppose we are given two
![]() $P_{\alpha }$
-names for reals,
$P_{\alpha }$
-names for reals,
![]() $\dot x$
and
$\dot x$
and
![]() $\dot x'$
, together with conditions
$\dot x'$
, together with conditions
![]() $p,p'$
, fusion sequences
$p,p'$
, fusion sequences
![]() $\bar S$
,
$\bar S$
,
![]() $\bar S'$
below
$\bar S'$
below
![]() $p,p'$
, respectively, fusion limits
$p,p'$
, respectively, fusion limits
![]() $p_\omega $
,
$p_\omega $
,
![]() $p_\omega '$
and associated partitions of
$p_\omega '$
and associated partitions of
![]() $\omega $
,
$\omega $
,
![]() $\bar Z$
and
$\bar Z$
and
![]() $\bar Z'$
, respectively, as in Lemma 4.1, such that
$\bar Z'$
, respectively, as in Lemma 4.1, such that
We call
![]() $\dot x$
and
$\dot x$
and
![]() $\dot x'$
isomorphic if there is an order isomorphism
$\dot x'$
isomorphic if there is an order isomorphism
such that
![]() $Z(\beta )=Z'(\pi (\beta ))$
and
$Z(\beta )=Z'(\pi (\beta ))$
and
![]() $T(\dot x,\bar S)=T(\dot x',\bar S') $
with the same sequence
$T(\dot x,\bar S)=T(\dot x',\bar S') $
with the same sequence
![]() $\bar t=\langle t_s: s\in \,^{<\omega }2\rangle $
of splitnodes. Then Definition 4.1(2) applies and we know that
$\bar t=\langle t_s: s\in \,^{<\omega }2\rangle $
of splitnodes. Then Definition 4.1(2) applies and we know that
![]() $\Omega (T(\dot x,\bar S))=\Omega (T(\dot x',\bar S'))$
and
$\Omega (T(\dot x,\bar S))=\Omega (T(\dot x',\bar S'))$
and
![]() $C(T(\dot x, \bar S))=C(T(\dot x',\bar S'))$
, i.e., isomorphic names are associated with the same coding system. Clearly, under CH there are only
$C(T(\dot x, \bar S))=C(T(\dot x',\bar S'))$
, i.e., isomorphic names are associated with the same coding system. Clearly, under CH there are only
![]() $\aleph _1$
-many isomorphism types of names.
$\aleph _1$
-many isomorphism types of names.
5 Extending the coding systems
As our goal is to prove cov
![]() $(\mathfrak {C}_2) =\aleph _1$
in the iterated Silver model, we need to construct a family of
$(\mathfrak {C}_2) =\aleph _1$
in the iterated Silver model, we need to construct a family of
![]() $\aleph _1$
-many coding systems coding
$\aleph _1$
-many coding systems coding
![]() $\mathfrak {C}_2$
-sets covering
$\mathfrak {C}_2$
-sets covering
![]() $2^\omega $
. For this, Lemma 4.1 is a good start, as any two isomorphic names of reals give rise to the same coding system as we have noticed at the end of Definition 4.2.
$2^\omega $
. For this, Lemma 4.1 is a good start, as any two isomorphic names of reals give rise to the same coding system as we have noticed at the end of Definition 4.2.
However, whenever by some forcing new reals are added then no dense
![]() $\Theta \subseteq \left [ \omega \right ] ^\omega $
in
$\Theta \subseteq \left [ \omega \right ] ^\omega $
in
![]() $\mathbf {V}$
will be dense in the extension (see the argument in the introduction). Hence the coding system
$\mathbf {V}$
will be dense in the extension (see the argument in the introduction). Hence the coding system
![]() $C(T(\bar Z))=\langle u^b:b\in \Omega (T(\bar Z))\rangle $
defined in Definition 4.1 where
$C(T(\bar Z))=\langle u^b:b\in \Omega (T(\bar Z))\rangle $
defined in Definition 4.1 where
![]() $T(\bar Z)=T(\dot x,\bar S)$
as in Lemma 4.1 has to be extended cofinally often during the iteration so that it will code a
$T(\bar Z)=T(\dot x,\bar S)$
as in Lemma 4.1 has to be extended cofinally often during the iteration so that it will code a
![]() $\mathfrak {C}_2$
-set A in the final model. This extension has to be done in such a way that Lemma 4.1 will remain true for every name belonging to the equivalence class
$\mathfrak {C}_2$
-set A in the final model. This extension has to be done in such a way that Lemma 4.1 will remain true for every name belonging to the equivalence class
![]() $\mathcal {K}$
of
$\mathcal {K}$
of
![]() $\dot x$
, i.e., the evaluation of every
$\dot x$
, i.e., the evaluation of every
![]() $\dot x '\in \mathcal {K}$
belongs to A.
$\dot x '\in \mathcal {K}$
belongs to A.
As is well-known, new reals appear only in intermediate models
![]() $\mathbf {V}^{P_{\gamma }}$
where
$\mathbf {V}^{P_{\gamma }}$
where
![]() $\gamma>0$
and cf
$\gamma>0$
and cf
![]() $(\gamma )$
is countable (i.e., finite and hence 1, or countably infinite). Hence at stages
$(\gamma )$
is countable (i.e., finite and hence 1, or countably infinite). Hence at stages
![]() $\gamma \leq \omega _2$
of uncountable cofinality we can take unions of the coding systems we already constructed. Hence we actively extend the coding systems only at steps
$\gamma \leq \omega _2$
of uncountable cofinality we can take unions of the coding systems we already constructed. Hence we actively extend the coding systems only at steps
![]() $\gamma>0$
of countable cofinality. In order to make sure that no old real is a branch through some new tree we are adding to the system at that stage, we make use of the
$\gamma>0$
of countable cofinality. In order to make sure that no old real is a branch through some new tree we are adding to the system at that stage, we make use of the
![]() $\gamma $
th Silver real
$\gamma $
th Silver real
![]() $\dot {g}_\gamma $
. Hence this extension will be completed only in the model
$\dot {g}_\gamma $
. Hence this extension will be completed only in the model
![]() $\mathbf {V}^{P_{\gamma +1}}$
.
$\mathbf {V}^{P_{\gamma +1}}$
.
We let
![]() $\Omega ^0(T(\bar Z))=\Omega (T(\bar Z))$
and
$\Omega ^0(T(\bar Z))=\Omega (T(\bar Z))$
and
![]() $C^{0}(T(\bar Z))=C(T(\bar Z))$
. So both belong to
$C^{0}(T(\bar Z))=C(T(\bar Z))$
. So both belong to
![]() $\mathbf {V}$
. Now we define
$\mathbf {V}$
. Now we define
![]() $\Omega ^{\gamma } (T)$
and the coding system
$\Omega ^{\gamma } (T)$
and the coding system
![]() $C^{\gamma } (T(\bar Z))=\langle u^{\dot {b}} :\dot {b}\in \Omega ^{\gamma } (T)\rangle $
for every
$C^{\gamma } (T(\bar Z))=\langle u^{\dot {b}} :\dot {b}\in \Omega ^{\gamma } (T)\rangle $
for every
![]() $0<\gamma <\omega _2$
such that
$0<\gamma <\omega _2$
such that
![]() $\Omega ^{\gamma } (T)\in \mathbf {V}^{P_{\gamma }}$
always and
$\Omega ^{\gamma } (T)\in \mathbf {V}^{P_{\gamma }}$
always and
![]() $C^{\gamma } (T(\bar Z))\in \mathbf {V}^{P_{\gamma }}$
if cf
$C^{\gamma } (T(\bar Z))\in \mathbf {V}^{P_{\gamma }}$
if cf
![]() $(\gamma )=\omega _1$
and
$(\gamma )=\omega _1$
and
![]() $C^{\gamma } (T(\bar Z))\in \mathbf {V}^{P_{\gamma +1}}$
if cf
$C^{\gamma } (T(\bar Z))\in \mathbf {V}^{P_{\gamma +1}}$
if cf
![]() $(\gamma )$
is countable.
$(\gamma )$
is countable.
Suppose we have already extended
![]() $C(T(\bar Z))$
to a coding system
$C(T(\bar Z))$
to a coding system
![]() $C^{\beta } (T(\bar Z))=\langle u^{\dot {b}} :\dot {b}\in \Omega ^{\beta } (T)\rangle $
in
$C^{\beta } (T(\bar Z))=\langle u^{\dot {b}} :\dot {b}\in \Omega ^{\beta } (T)\rangle $
in
![]() $\mathbf {V}^{P_{\beta +1}}$
for every
$\mathbf {V}^{P_{\beta +1}}$
for every
![]() $\beta <\gamma $
, for some
$\beta <\gamma $
, for some
![]() $0<\gamma <\omega _2$
. If
$0<\gamma <\omega _2$
. If
![]() $\gamma $
is a limit of uncountable cofinality we let
$\gamma $
is a limit of uncountable cofinality we let
and
If
![]() $ \gamma $
has countable cofinality, let
$ \gamma $
has countable cofinality, let
 $$ \begin{align*}\Omega^{\gamma }(T(\bar Z))=\lbrace \dot{b}\in \Omega (T(\bar Z)) ^{\mathbf{V}^{P_{\gamma }}}: \lnot\,\,\exists c\in \left[\omega \right] ^\omega \cap \bigcup_{\beta<\gamma}\mathbf{V}^{P_\beta} \quad c\subseteq\dot{b} \rbrace.\end{align*} $$
$$ \begin{align*}\Omega^{\gamma }(T(\bar Z))=\lbrace \dot{b}\in \Omega (T(\bar Z)) ^{\mathbf{V}^{P_{\gamma }}}: \lnot\,\,\exists c\in \left[\omega \right] ^\omega \cap \bigcup_{\beta<\gamma}\mathbf{V}^{P_\beta} \quad c\subseteq\dot{b} \rbrace.\end{align*} $$
(For the definition of
![]() $\Omega (T(\bar Z))$
see Definition 4.1(1).) Clearly,
$\Omega (T(\bar Z))$
see Definition 4.1(1).) Clearly,
![]() $\Omega ^{\gamma }(T(\bar Z))$
is dense in
$\Omega ^{\gamma }(T(\bar Z))$
is dense in
![]() $\left [\omega \right ] ^\omega \cap \mathbf {V}^{P_{\gamma }}$
. In this case, in
$\left [\omega \right ] ^\omega \cap \mathbf {V}^{P_{\gamma }}$
. In this case, in
![]() $\mathbf {V}^{P_{\gamma +1}}$
we shall define a coding system
$\mathbf {V}^{P_{\gamma +1}}$
we shall define a coding system
![]() $\langle u^{\dot {b}}: \dot {b}\in \Omega ^{\gamma }(T(\bar Z))\rangle $
such that for every
$\langle u^{\dot {b}}: \dot {b}\in \Omega ^{\gamma }(T(\bar Z))\rangle $
such that for every
![]() $\dot x'\in \mathcal {K}$
(with associated isomorphism
$\dot x'\in \mathcal {K}$
(with associated isomorphism
![]() $\pi '$
, fusion sequence
$\pi '$
, fusion sequence
![]() $\bar S'$
and limit
$\bar S'$
and limit
![]() $p^{\prime }_\omega $
), its evaluation in the final model is not a branch through any of the
$p^{\prime }_\omega $
), its evaluation in the final model is not a branch through any of the
![]() $u^{\dot {b}}$
.
$u^{\dot {b}}$
.
As in Definition 4.1, the definition of
![]() $u^{\dot {b}}$
will depend on the three types of members of
$u^{\dot {b}}$
will depend on the three types of members of
![]() $\Omega ^{\gamma }(T(\bar Z))$
. But now, the two first ones of these (i.e.,
$\Omega ^{\gamma }(T(\bar Z))$
. But now, the two first ones of these (i.e.,
![]() $\dot {b}\subset L(\beta )$
for some
$\dot {b}\subset L(\beta )$
for some
![]() $\beta \in \mathrm {supp}(p_\omega )$
or
$\beta \in \mathrm {supp}(p_\omega )$
or
![]() $\dot {b}\subseteq \bigcup _{\beta \in \mathrm {supp}(p_\omega )}L(\beta )$
and
$\dot {b}\subseteq \bigcup _{\beta \in \mathrm {supp}(p_\omega )}L(\beta )$
and
![]() $\forall \beta \in \mathrm {supp}(p_\omega )\,\vert \dot {b}\cap L(\beta )\vert \leq 1$
) split into two subcases taking care of how
$\forall \beta \in \mathrm {supp}(p_\omega )\,\vert \dot {b}\cap L(\beta )\vert \leq 1$
) split into two subcases taking care of how
![]() $\mathrm {supp} (p_\omega ')$
and
$\mathrm {supp} (p_\omega ')$
and
![]() $\pi '(\beta )$
are positioned with respect to
$\pi '(\beta )$
are positioned with respect to
![]() $\gamma $
. For this, disjoint infinite subsets
$\gamma $
. For this, disjoint infinite subsets
![]() $\dot {b}_0,\dot {b}_1$
of
$\dot {b}_0,\dot {b}_1$
of
![]() $\dot {b}$
are chosen and then, on levels from
$\dot {b}$
are chosen and then, on levels from
![]() $\dot {b}_0$
,
$\dot {b}_0$
,
![]() $u^{\dot {b}} $
is defined in
$u^{\dot {b}} $
is defined in
![]() $\mathbf {V}^{P_\gamma }$
, whereas on levels from
$\mathbf {V}^{P_\gamma }$
, whereas on levels from
![]() $\dot {b}_1$
we need the Silver real
$\dot {b}_1$
we need the Silver real
![]() $\dot {g}_\gamma $
to define it.
$\dot {g}_\gamma $
to define it.
For our main result we shall need to know that in the Silver model, the ground model reals are a
![]() $\mathfrak {P}_2$
-set. This seems to be proved by [Reference Cichoń, Rosłanowski, Steprāns and Weglorz2, Corollary 4.4] by using the Sacks property of
$\mathfrak {P}_2$
-set. This seems to be proved by [Reference Cichoń, Rosłanowski, Steprāns and Weglorz2, Corollary 4.4] by using the Sacks property of
![]() $\mathbb {SI}$
. Let us give a direct proof here.
$\mathbb {SI}$
. Let us give a direct proof here.
Lemma 5.1. Suppose that
![]() $f_0\in \mathbb {SI}$
and
$f_0\in \mathbb {SI}$
and
![]() $\dot b$
is a
$\dot b$
is a
![]() $\mathbb {SI}$
-name such that
$\mathbb {SI}$
-name such that
![]() $f_0\Vdash _{\mathbb {SI}} \,\dot {b}\in [\omega ] ^\omega .$
There exist
$f_0\Vdash _{\mathbb {SI}} \,\dot {b}\in [\omega ] ^\omega .$
There exist
![]() $\mathbb {SI}$
-names
$\mathbb {SI}$
-names
![]() $\dot c, \dot y$
and a condition
$\dot c, \dot y$
and a condition
![]() $f\in \mathbb {SI}$
such that
$f\in \mathbb {SI}$
such that
![]() $f\leq f_0$
and
$f\leq f_0$
and
Proof. By a simple fusion we can find
![]() $f\in \mathbb {SI}$
and a one-to-one family
$f\in \mathbb {SI}$
and a one-to-one family
![]() $\langle k_s:s\in \, ^{<\omega } 2\rangle $
in
$\langle k_s:s\in \, ^{<\omega } 2\rangle $
in
![]() $\omega $
such that
$\omega $
such that
![]() $f\leq f_0$
and
$f\leq f_0$
and
for every
![]() $s\in \, ^{<\omega } 2$
. Letting
$s\in \, ^{<\omega } 2$
. Letting
![]() $\dot g$
be the canonical name for the Silver real and defining
$\dot g$
be the canonical name for the Silver real and defining
clearly
![]() $f\Vdash _{\mathbb {SI}}\, \dot c\in [ \dot b ] ^{\omega }$
. Now we define
$f\Vdash _{\mathbb {SI}}\, \dot c\in [ \dot b ] ^{\omega }$
. Now we define
![]() $\dot y $
on
$\dot y $
on
![]() $\dot c$
such that
$\dot c$
such that
Given any
![]() $f'\leq f$
and
$f'\leq f$
and
![]() $x\in \,^\omega 2\cap \mathbf {V}$
, let s be maximal with
$x\in \,^\omega 2\cap \mathbf {V}$
, let s be maximal with
![]() $f'\leq f^s$
and let
$f'\leq f^s$
and let
![]() $j=\min (\mathrm {com}(f'))$
. Hence
$j=\min (\mathrm {com}(f'))$
. Hence
![]() $f'\Vdash _{\mathbb {SI}} k_s\in \dot c$
, and
$f'\Vdash _{\mathbb {SI}} k_s\in \dot c$
, and
![]() $\dot y(k_s)$
depends on
$\dot y(k_s)$
depends on
![]() $\dot g(j)$
, thus has not yet been decided by
$\dot g(j)$
, thus has not yet been decided by
![]() $f'$
. Hence we can find
$f'$
. Hence we can find
![]() $f"\leq f'$
forcing
$f"\leq f'$
forcing
![]() $\dot y(k_s)\ne x(k_s)$
. Note that the lemma is nontrivial only if
$\dot y(k_s)\ne x(k_s)$
. Note that the lemma is nontrivial only if
![]() $\dot {b}$
is forced to be outside
$\dot {b}$
is forced to be outside
![]() $\mathbf {V}$
.
$\mathbf {V}$
.
Corollary 5.1. (1)
![]() $\mathbf {V}^{\mathbb {SI}}\models \; ^\omega 2\cap \mathbf {V} \in \mathfrak {P}_2$
.
$\mathbf {V}^{\mathbb {SI}}\models \; ^\omega 2\cap \mathbf {V} \in \mathfrak {P}_2$
.
(2) If
![]() $P_{\omega _2}$
is the CS iteration of
$P_{\omega _2}$
is the CS iteration of
![]() $\mathbb {SI}$
of length
$\mathbb {SI}$
of length
![]() $\omega _2$
then
$\omega _2$
then
![]() $\mathbf {V}^{P_{\omega _2}}\models \; ^\omega 2\cap \mathbf {V} \in \mathfrak {P}_2.$
$\mathbf {V}^{P_{\omega _2}}\models \; ^\omega 2\cap \mathbf {V} \in \mathfrak {P}_2.$
Proof. (1) In
![]() $\mathbf {V}^{\mathbb {SI}}$
, let
$\mathbf {V}^{\mathbb {SI}}$
, let
![]() $\Theta \subseteq \,^\omega [\omega ]$
be dense such that for every
$\Theta \subseteq \,^\omega [\omega ]$
be dense such that for every
![]() $b\in \Theta $
we have
$b\in \Theta $
we have
![]() $[b]^\omega \cap \mathbf {V} =\emptyset $
. By Lemma 5.1, for every
$[b]^\omega \cap \mathbf {V} =\emptyset $
. By Lemma 5.1, for every
![]() $b\in \Theta $
find a Silver function
$b\in \Theta $
find a Silver function
![]() $f^b$
with dom
$f^b$
with dom
![]() $(f^ b)=b$
such that for no
$(f^ b)=b$
such that for no
![]() $x\in \, ^\omega 2\cap \mathbf {V}$
,
$x\in \, ^\omega 2\cap \mathbf {V}$
,
![]() $x\upharpoonright b =f^b$
. Then
$x\upharpoonright b =f^b$
. Then
![]() $C=\langle f^b:b\in \Theta \rangle $
codes the
$C=\langle f^b:b\in \Theta \rangle $
codes the
![]() $\mathfrak {P}_2$
-set
$\mathfrak {P}_2$
-set
which has the property
![]() $^\omega 2\cap \mathbf {V}\subseteq A(C )$
.
$^\omega 2\cap \mathbf {V}\subseteq A(C )$
.
(2) For every
![]() $\gamma <\omega _2$
, in
$\gamma <\omega _2$
, in
![]() $\mathbf {V}^{P_{\gamma +1}}$
we can choose a dense
$\mathbf {V}^{P_{\gamma +1}}$
we can choose a dense
![]() $\Omega ^{\gamma +1} \subseteq \left [ \omega \right ] ^\omega $
such that for every
$\Omega ^{\gamma +1} \subseteq \left [ \omega \right ] ^\omega $
such that for every
![]() $b\in \Omega ^{\gamma +1} $
,
$b\in \Omega ^{\gamma +1} $
,
![]() $\left [ b\right ] ^\omega \cap \mathbf {V}^{P_{\gamma }} =\emptyset $
, and then, as in (1), define a coding system
$\left [ b\right ] ^\omega \cap \mathbf {V}^{P_{\gamma }} =\emptyset $
, and then, as in (1), define a coding system
![]() $C^{\gamma +1} =\langle f^b:b\in \Omega ^{\gamma +1} \rangle $
such that
$C^{\gamma +1} =\langle f^b:b\in \Omega ^{\gamma +1} \rangle $
such that
![]() $^\omega 2\cap \mathbb {V}^{P_\gamma }\subseteq A(C^{\gamma +1} )$
. In
$^\omega 2\cap \mathbb {V}^{P_\gamma }\subseteq A(C^{\gamma +1} )$
. In
![]() $\mathbf {V}^{P_{\omega _2}}$
we have the coding system
$\mathbf {V}^{P_{\omega _2}}$
we have the coding system
![]() $C=\langle f^b: b\in \Omega ^{\gamma +1} , \gamma <\omega _2\rangle $
defining the
$C=\langle f^b: b\in \Omega ^{\gamma +1} , \gamma <\omega _2\rangle $
defining the
![]() $\mathfrak {P}_2$
-set
$\mathfrak {P}_2$
-set
![]() $A(C)$
which covers
$A(C)$
which covers
![]() $^\omega 2\cap \mathbf {V} $
.
$^\omega 2\cap \mathbf {V} $
.
Remark 5.1. In [Reference Cichoń, Rosłanowski, Steprāns and Weglorz2, Proposition 4.13] it is shown that Corollary 5.1(1) is false for Laver as well as for Miller forcing.
Now the precise crucial definition of how we extend our coding systems along the iteration is as follows.
Definition 5.1. Suppose that in
![]() $\mathbf {V} $
we are given some coding tree
$\mathbf {V} $
we are given some coding tree
![]() $T(\bar Z)$
. Recall that in particular
$T(\bar Z)$
. Recall that in particular
![]() $\bar Z=\langle Z(\beta ): \beta \in Y\rangle $
is a partition of
$\bar Z=\langle Z(\beta ): \beta \in Y\rangle $
is a partition of
![]() $\omega $
into infinite sets,
$\omega $
into infinite sets,
![]() $\bar t=\langle t_s: s\in \,^{<\omega }2\rangle $
canonically enumerates
$\bar t=\langle t_s: s\in \,^{<\omega }2\rangle $
canonically enumerates
![]() $\mathrm {split}(T(\bar Z))$
and
$\mathrm {split}(T(\bar Z))$
and
![]() $L(\beta )=\left \lbrace \vert t_s\vert : \vert s\vert \in Z(\beta )\right \rbrace $
. Let
$L(\beta )=\left \lbrace \vert t_s\vert : \vert s\vert \in Z(\beta )\right \rbrace $
. Let
![]() $\dot x$
with fusion
$\dot x$
with fusion
![]() $\bar S$
and limit
$\bar S$
and limit
![]() $p_\omega $
be associated with
$p_\omega $
be associated with
![]() $T(\bar Z)$
, so in particular
$T(\bar Z)$
, so in particular
![]() $\mathrm {supp} (p_\omega )=Y$
and
$\mathrm {supp} (p_\omega )=Y$
and
![]() $T(\bar Z)=T(\dot x,\bar S)$
. Let
$T(\bar Z)=T(\dot x,\bar S)$
. Let
![]() $A_n(\bar {S})=\langle a^s=a^s(\bar {S}): s\in \,^{n}2\rangle $
for
$A_n(\bar {S})=\langle a^s=a^s(\bar {S}): s\in \,^{n}2\rangle $
for
![]() $n<\omega $
be the associated refining maximal antichains below
$n<\omega $
be the associated refining maximal antichains below
![]() $p_\omega $
(see Remark 2.1(3)). Let
$p_\omega $
(see Remark 2.1(3)). Let
![]() $\pi =\mathrm { id}_Y$
.
$\pi =\mathrm { id}_Y$
.
Let
![]() $\mathcal {K} $
be the isomorphism class of names associated with
$\mathcal {K} $
be the isomorphism class of names associated with
![]() $T(\bar Z)$
. For
$T(\bar Z)$
. For
![]() $\dot x' \in \mathcal {K}$
let
$\dot x' \in \mathcal {K}$
let
![]() $\bar S'$
be the associated fusion,
$\bar S'$
be the associated fusion,
![]() $p_\omega '$
its limit,
$p_\omega '$
its limit,
![]() $\pi ' :Y \rightarrow \mathrm {supp}(p_\omega ')$
the isomorphism and
$\pi ' :Y \rightarrow \mathrm {supp}(p_\omega ')$
the isomorphism and
![]() $A_n(\bar {S}')=\langle a^s(\bar {S}'): s\in \,^{n}2\rangle $
the associated maximal antichains below
$A_n(\bar {S}')=\langle a^s(\bar {S}'): s\in \,^{n}2\rangle $
the associated maximal antichains below
![]() $p_\omega '$
. Moreover, let
$p_\omega '$
. Moreover, let
![]() $\dot {g}_\gamma \in \mathbf {V}^{P_{\gamma +1}}$
be the Silver real added by the iterand
$\dot {g}_\gamma \in \mathbf {V}^{P_{\gamma +1}}$
be the Silver real added by the iterand
![]() $\dot Q_\gamma $
of the iteration.
$\dot Q_\gamma $
of the iteration.
Given any
![]() $ {b}\subseteq \omega $
, define
$ {b}\subseteq \omega $
, define
![]() $Z(b)=\left \lbrace \vert s\vert : \vert t_s\vert \in b\right \rbrace .$
Note that it may happen that there are s with
$Z(b)=\left \lbrace \vert s\vert : \vert t_s\vert \in b\right \rbrace .$
Note that it may happen that there are s with
![]() $\vert s\vert \in Z(b)$
but
$\vert s\vert \in Z(b)$
but
![]() $\vert t_s\vert \not \in b$
(see property (ii) of a coding tree).
$\vert t_s\vert \not \in b$
(see property (ii) of a coding tree).
For every
![]() $\gamma <\omega _2$
, in
$\gamma <\omega _2$
, in
![]() $\mathbf {V}^{P_{\gamma }}$
we have already defined
$\mathbf {V}^{P_{\gamma }}$
we have already defined
![]() $\Omega ^{\gamma }(T(\bar Z))$
at the beginning of this section. Now let us define the coding system
$\Omega ^{\gamma }(T(\bar Z))$
at the beginning of this section. Now let us define the coding system
in
![]() $\mathbf {V}^{P_{\gamma +1}}$
. For
$\mathbf {V}^{P_{\gamma +1}}$
. For
![]() $\dot {b}\in \Omega ^{\gamma }(T(\bar Z))$
,
$\dot {b}\in \Omega ^{\gamma }(T(\bar Z))$
,
![]() $u^{\dot {b}}$
will be defined according to the three types of members of
$u^{\dot {b}}$
will be defined according to the three types of members of
![]() $ \Omega ^{\gamma }(T(\bar Z))$
. Always,
$ \Omega ^{\gamma }(T(\bar Z))$
. Always,
![]() $u^{\dot {b}}$
will be defined as a uniform tree with
$u^{\dot {b}}$
will be defined as a uniform tree with
![]() $a^{u^{\dot {b}}}=\omega \setminus {\dot {b}}$
.
$a^{u^{\dot {b}}}=\omega \setminus {\dot {b}}$
.
(I) Suppose
![]() ${\dot {b}}\in \Omega ^{\gamma }(T(\bar Z))$
is such that
${\dot {b}}\in \Omega ^{\gamma }(T(\bar Z))$
is such that
![]() ${\dot {b}}\subseteq L(\beta ) $
for some
${\dot {b}}\subseteq L(\beta ) $
for some
![]() $\beta \in Y$
. In
$\beta \in Y$
. In
![]() $\mathbf {V}^{P_{\gamma }}$
, let
$\mathbf {V}^{P_{\gamma }}$
, let
![]() ${\dot {b}}={\dot {b}}_0\cup {\dot {b}}_1 $
be a partition into two infinite sets. Levels of
${\dot {b}}={\dot {b}}_0\cup {\dot {b}}_1 $
be a partition into two infinite sets. Levels of
![]() $u^{\dot {b}}$
in
$u^{\dot {b}}$
in
![]() ${\dot {b}}_0$
are defined in
${\dot {b}}_0$
are defined in
![]() $\mathbf {V} ^{P_{\gamma }}$
while levels in
$\mathbf {V} ^{P_{\gamma }}$
while levels in
![]() ${\dot {b}}_1$
are defined in
${\dot {b}}_1$
are defined in
![]() $\mathbf {V} ^{P_{\gamma +1}}$
. More precisely, for every
$\mathbf {V} ^{P_{\gamma +1}}$
. More precisely, for every
![]() $l\in {\dot {b}}_0$
and
$l\in {\dot {b}}_0$
and
![]() $t\in \,^l2$
, at first we define a next digit
$t\in \,^l2$
, at first we define a next digit
![]() $d(t)<2$
(in
$d(t)<2$
(in
![]() $\mathbf {V}^{P_{\gamma }}$
). Then, in
$\mathbf {V}^{P_{\gamma }}$
). Then, in
![]() $\mathbf {V}^{P_{\gamma +1}}$
, for every
$\mathbf {V}^{P_{\gamma +1}}$
, for every
![]() $l\in {\dot {b}}_1$
and
$l\in {\dot {b}}_1$
and
![]() $t\in \,^l2$
a next digit
$t\in \,^l2$
a next digit
![]() $d(t)$
will be defined. Then, in
$d(t)$
will be defined. Then, in
![]() $\mathbf {V} ^{P_{\gamma +1}}$
,
$\mathbf {V} ^{P_{\gamma +1}}$
,
![]() $u^{\dot {b}}$
will be the non-empty uniform tree such that for every
$u^{\dot {b}}$
will be the non-empty uniform tree such that for every
![]() $t\in u^{\dot {b}}$
, if
$t\in u^{\dot {b}}$
, if
![]() $\vert t\vert \in {\dot {b}}$
, then its next digit is
$\vert t\vert \in {\dot {b}}$
, then its next digit is
![]() $d(t)$
.
$d(t)$
.
-
(0) (On levels from
 ${\dot {b}}_0$
we make sure that we can deal with
${\dot {b}}_0$
we make sure that we can deal with
 $\dot {x}'\in \mathcal {K} $
with associated isomorphism
$\dot {x}'\in \mathcal {K} $
with associated isomorphism
 $\pi '$
such that
$\pi '$
such that
 $\gamma \leq \pi '(\beta )$
.) On levels in
$\gamma \leq \pi '(\beta )$
.) On levels in
 ${\dot {b}}_0$
we define
${\dot {b}}_0$
we define
 $u^{\dot {b}}$
in
$u^{\dot {b}}$
in
 $\mathbf {V}^{P_{\gamma }}$
analogously as in Definition 4.1(1)(I): Suppose
$\mathbf {V}^{P_{\gamma }}$
analogously as in Definition 4.1(1)(I): Suppose
 $l\in {\dot {b}}_0$
and
$l\in {\dot {b}}_0$
and
 $t\in \, ^{l}2$
. Then
$t\in \, ^{l}2$
. Then
 $d(t)$
is determined as follows:
$d(t)$
is determined as follows:-
• if
 $t\not \in T(\bar Z)$
let
$t\not \in T(\bar Z)$
let
 $d(t)=0 $
;
$d(t)=0 $
; -
• if
 $t \in T(\bar Z)\setminus \mathrm {split}(T(\bar Z))$
let
$t \in T(\bar Z)\setminus \mathrm {split}(T(\bar Z))$
let
 $d(t)$
be such that
$d(t)$
be such that
 $t\,^\smallfrown \, d(t)\not \in T(\bar Z)$
;
$t\,^\smallfrown \, d(t)\not \in T(\bar Z)$
; -
• if
 $t\in \mathrm {split}(T(\bar Z))$
, thus
$t\in \mathrm {split}(T(\bar Z))$
, thus
 $t=t_s$
for some
$t=t_s$
for some
 $s\in \,^{<\omega }2$
, letting we stipulate that
$s\in \,^{<\omega }2$
, letting we stipulate that $$ \begin{align*}i(t,\beta):= \vert \left\lbrace j\in \vert s\vert \cap Z(\beta) :s(j)=1\right\rbrace \vert \,\mathrm{mod}\,2,\end{align*} $$
$$ \begin{align*}i(t,\beta):= \vert \left\lbrace j\in \vert s\vert \cap Z(\beta) :s(j)=1\right\rbrace \vert \,\mathrm{mod}\,2,\end{align*} $$
 $$ \begin{align*}d(t)= t_{s\,^\smallfrown\, i(t,\beta)}(\vert t\vert ) .\end{align*} $$
$$ \begin{align*}d(t)= t_{s\,^\smallfrown\, i(t,\beta)}(\vert t\vert ) .\end{align*} $$
-
-
(1) (On levels from
 ${\dot {b}}_1$
, we take care of those
${\dot {b}}_1$
, we take care of those
 $\dot {x}'$
with
$\dot {x}'$
with
 $\pi '(\beta ) <\gamma $
.) In
$\pi '(\beta ) <\gamma $
.) In
 $\mathbf {V} ^{P_{\gamma +1}}$
we can choose a real
$\mathbf {V} ^{P_{\gamma +1}}$
we can choose a real
 $\dot {h}:Z({\dot {b}}_1)\rightarrow 2$
such that
$\dot {h}:Z({\dot {b}}_1)\rightarrow 2$
such that
 $\dot {h}\not \in \mathbf {V}^{P_{\gamma }}$
, e.g., if
$\dot {h}\not \in \mathbf {V}^{P_{\gamma }}$
, e.g., if
 $\dot {\rho } :Z({\dot {b}}_1 ) \rightarrow \omega $
is a bijection in
$\dot {\rho } :Z({\dot {b}}_1 ) \rightarrow \omega $
is a bijection in
 $\mathbf {V}^{P_{\gamma }}$
, let
$\mathbf {V}^{P_{\gamma }}$
, let
 $\dot {h}=\dot {g}_\gamma \circ \dot {\rho }$
.
$\dot {h}=\dot {g}_\gamma \circ \dot {\rho }$
.Now suppose
 $l\in {\dot {b}}_1$
and
$l\in {\dot {b}}_1$
and
 $t\in u^{\dot {b}}\cap \,^{l}2$
. Define
$t\in u^{\dot {b}}\cap \,^{l}2$
. Define
 $d(t)<2$
as follows:
$d(t)<2$
as follows:-
• if
 $t\not \in T(\bar Z)$
let
$t\not \in T(\bar Z)$
let
 $d(t)=0 $
;
$d(t)=0 $
; -
• if
 $t \in T(\bar Z)\setminus \mathrm {split}(T(\bar Z))$
let
$t \in T(\bar Z)\setminus \mathrm {split}(T(\bar Z))$
let
 $d(t) $
such that
$d(t) $
such that
 $t\,^\smallfrown \, d(t)\not \in T(\bar Z)$
;
$t\,^\smallfrown \, d(t)\not \in T(\bar Z)$
; -
• if
 $t\in \mathrm {split}(T(\bar Z))$
, hence
$t\in \mathrm {split}(T(\bar Z))$
, hence
 $t=t_s$
for some s, and
$t=t_s$
for some s, and
 $\vert s\vert =i\in Z({\dot {b}}_1)$
for some i, we let
$\vert s\vert =i\in Z({\dot {b}}_1)$
for some i, we let  $$ \begin{align*}d(t)= t_{s\,^\smallfrown\, h(i)}(\vert t\vert ) .\end{align*} $$
$$ \begin{align*}d(t)= t_{s\,^\smallfrown\, h(i)}(\vert t\vert ) .\end{align*} $$
-
(II) Suppose
![]() ${\dot {b}}\in \Omega ^{\gamma }(T(\bar Z))$
is such that
${\dot {b}}\in \Omega ^{\gamma }(T(\bar Z))$
is such that
![]() $\forall \beta \in Y\; \vert {\dot {b}}\cap L(\beta ) \vert \leq 1$
and
$\forall \beta \in Y\; \vert {\dot {b}}\cap L(\beta ) \vert \leq 1$
and
![]() ${\dot {b}}\subseteq \bigcup \left \lbrace L(\beta ):\beta \in Y\right \rbrace $
. For
${\dot {b}}\subseteq \bigcup \left \lbrace L(\beta ):\beta \in Y\right \rbrace $
. For
![]() $b_*\subseteq {\dot {b}}$
let
$b_*\subseteq {\dot {b}}$
let
Clearly,
![]() $Y({\dot {b}})\in \mathbf {V}^{P_{\gamma }}$
is infinite. Note that for any
$Y({\dot {b}})\in \mathbf {V}^{P_{\gamma }}$
is infinite. Note that for any
![]() $\dot {x}'\in \mathcal {K}$
we have
$\dot {x}'\in \mathcal {K}$
we have
(See Definition 4.1(2).) Let
![]() $\dot {\delta } $
be the largest accumulation point of
$\dot {\delta } $
be the largest accumulation point of
![]() $Y(\dot {b})$
. It is easy to choose
$Y(\dot {b})$
. It is easy to choose
![]() $ {\dot {b}}_0$
and
$ {\dot {b}}_0$
and
![]() ${\dot {b}}_1$
in
${\dot {b}}_1$
in
![]() $\mathbf {V}^{P_{\gamma }}$
such that
$\mathbf {V}^{P_{\gamma }}$
such that
![]() ${\dot {b}}_0$
and
${\dot {b}}_0$
and
![]() ${\dot {b}}_1$
are disjoint infinite subsets of
${\dot {b}}_1$
are disjoint infinite subsets of
![]() ${\dot {b}}$
with
${\dot {b}}$
with
![]() $\sup (Y({\dot {b}}_0))=\sup (Y({\dot {b}}_1)) =\dot \delta $
and
$\sup (Y({\dot {b}}_0))=\sup (Y({\dot {b}}_1)) =\dot \delta $
and
![]() $\dot \delta \not \in Y({\dot {b}}_0\cup {\dot {b}}_1)$
. As in Case I, on the levels in
$\dot \delta \not \in Y({\dot {b}}_0\cup {\dot {b}}_1)$
. As in Case I, on the levels in
![]() ${\dot {b}}_0$
,
${\dot {b}}_0$
,
![]() $u^{\dot {b}}$
will be defined in
$u^{\dot {b}}$
will be defined in
![]() $\mathbf {V}^{P_{\gamma }}$
, while its levels in
$\mathbf {V}^{P_{\gamma }}$
, while its levels in
![]() ${\dot {b}}_1$
will be defined in
${\dot {b}}_1$
will be defined in
![]() $\mathbf {V}^{P_{\gamma +1}}$
, by defining a next-digit-function d on
$\mathbf {V}^{P_{\gamma +1}}$
, by defining a next-digit-function d on
![]() $\bigcup _{l\in {\dot {b}}_0}\,^l2$
,
$\bigcup _{l\in {\dot {b}}_0}\,^l2$
,
![]() $\bigcup _{l\in {\dot {b}}_1}\,^l2$
,
$\bigcup _{l\in {\dot {b}}_1}\,^l2$
,
![]() $\bigcup _{l\in \dot {b}\setminus (\dot {b}_0\cup \dot {b}_1})\,^l2$
, respectively, and then letting
$\bigcup _{l\in \dot {b}\setminus (\dot {b}_0\cup \dot {b}_1})\,^l2$
, respectively, and then letting
![]() $u^{\dot {b}}$
be the non-empty tree such that for every
$u^{\dot {b}}$
be the non-empty tree such that for every
![]() $t\in u^{\dot {b}}$
with
$t\in u^{\dot {b}}$
with
![]() $\vert t\vert \in {\dot {b}}$
, its next digit is
$\vert t\vert \in {\dot {b}}$
, its next digit is
![]() $d(t)$
.
$d(t)$
.
-
(0) (On levels from
 ${\dot {b}}_0$
we take care of
${\dot {b}}_0$
we take care of
 $\dot x'\in \mathcal {K}$
such that we have
$\dot x'\in \mathcal {K}$
such that we have
 $\sup (\pi [Y({\dot {b}}_0)]) \geq \gamma +1 $
, and hence
$\sup (\pi [Y({\dot {b}}_0)]) \geq \gamma +1 $
, and hence
 $\sup (\pi [Y({\dot {b}}_0)])>\gamma +1 $
.) We define
$\sup (\pi [Y({\dot {b}}_0)])>\gamma +1 $
.) We define
 $u^{\dot {b}}$
on levels from
$u^{\dot {b}}$
on levels from
 ${\dot {b}}_0$
as in Definition 4.1(II): Given
${\dot {b}}_0$
as in Definition 4.1(II): Given
 $t\in \,^l2$
with
$t\in \,^l2$
with
 $l\in {\dot {b}}_0$
,
$l\in {\dot {b}}_0$
,
 $d(t)$
is determined such that
$d(t)$
is determined such that-
• if
 $t\not \in T(\bar Z)$
or
$t\not \in T(\bar Z)$
or
 $t\in \mathrm {split}(T(\bar Z))$
then
$t\in \mathrm {split}(T(\bar Z))$
then
 $d(t)= 0 $
;
$d(t)= 0 $
; -
• if
 $t \in T(\bar Z)\setminus \mathrm {split}(T(\bar Z))$
,
$t \in T(\bar Z)\setminus \mathrm {split}(T(\bar Z))$
,
 $d(t)<2$
is defined such that
$d(t)<2$
is defined such that
 $t\,^\smallfrown \, d(t)\not \in T(\bar Z)$
.
$t\,^\smallfrown \, d(t)\not \in T(\bar Z)$
.
-
-
(1) (On levels from
 ${\dot {b}}_1$
we take care of
${\dot {b}}_1$
we take care of
 $\dot x'\in \mathcal {K}$
such that we have
$\dot x'\in \mathcal {K}$
such that we have
 $\sup (\pi ' [Y({\dot {b}}_0)]) \leq \gamma $
.) Then
$\sup (\pi ' [Y({\dot {b}}_0)]) \leq \gamma $
.) Then
 $Z({\dot {b}}_1)\in \mathbf {V}^{P_{\gamma }}$
(see the beginning of the present definition for its definition). We choose
$Z({\dot {b}}_1)\in \mathbf {V}^{P_{\gamma }}$
(see the beginning of the present definition for its definition). We choose
 $\dot h:{Z({\dot {b}}_1)}\rightarrow 2$
in
$\dot h:{Z({\dot {b}}_1)}\rightarrow 2$
in
 $\mathbf {V}^{P_{\gamma +1}}$
such that for no
$\mathbf {V}^{P_{\gamma +1}}$
such that for no
 $x:Z({\dot {b}}_1)\rightarrow 2$
in
$x:Z({\dot {b}}_1)\rightarrow 2$
in
 $ \mathbf {V}^{P_{\gamma }}$
we have
$ \mathbf {V}^{P_{\gamma }}$
we have
 $x =\dot h$
. Now suppose
$x =\dot h$
. Now suppose
 $l\in {\dot {b}}_1$
and
$l\in {\dot {b}}_1$
and
 $t\in \,^l2$
. Then
$t\in \,^l2$
. Then
 $d(t)$
is defined as follows:
$d(t)$
is defined as follows:-
• if
 $t\not \in T(\bar Z)$
let
$t\not \in T(\bar Z)$
let
 $d(t)= 0 $
;
$d(t)= 0 $
; -
• if
 $t \in T(\bar Z)\setminus \mathrm {split}(T(\bar Z))$
let
$t \in T(\bar Z)\setminus \mathrm {split}(T(\bar Z))$
let
 $d(t)<2$
such that
$d(t)<2$
such that
 $t\,^\smallfrown \, d(t)\not \in T(\bar Z)$
;
$t\,^\smallfrown \, d(t)\not \in T(\bar Z)$
; -
• if
 $t\in \mathrm {split}(T(\bar Z))$
, thus
$t\in \mathrm {split}(T(\bar Z))$
, thus
 $t=t_s$
for some
$t=t_s$
for some
 $s\in \,^{<\omega }2$
(and
$s\in \,^{<\omega }2$
(and
 $\vert s\vert \in Z({\dot {b}}_1 )$
), we let
$\vert s\vert \in Z({\dot {b}}_1 )$
), we let  $$ \begin{align*}d(t)= t_{s\,^\smallfrown\, \dot h(\vert s\vert)}(\vert t\vert ) .\end{align*} $$
$$ \begin{align*}d(t)= t_{s\,^\smallfrown\, \dot h(\vert s\vert)}(\vert t\vert ) .\end{align*} $$
-
-
(2) For
 $t\in u^{\dot {b}}$
with
$t\in u^{\dot {b}}$
with
 $\vert t\vert \in {\dot {b}}\setminus ({\dot {b}}_0\cup {\dot {b}}_1)$
, its next digit in
$\vert t\vert \in {\dot {b}}\setminus ({\dot {b}}_0\cup {\dot {b}}_1)$
, its next digit in
 $u^{\dot {b}}$
is irrelevant, we require that it is
$u^{\dot {b}}$
is irrelevant, we require that it is
 $0$
.
$0$
.
(III) Suppose
![]() ${\dot {b}}\in \Omega ^{\gamma }(T(\bar Z))$
is such that
${\dot {b}}\in \Omega ^{\gamma }(T(\bar Z))$
is such that
![]() ${\dot {b}}\cap \bigcup \left \lbrace L(\beta ):\beta \in Y\right \rbrace =\emptyset $
. Hence no splitnode of
${\dot {b}}\cap \bigcup \left \lbrace L(\beta ):\beta \in Y\right \rbrace =\emptyset $
. Hence no splitnode of
![]() $T(\bar Z)$
has its length in
$T(\bar Z)$
has its length in
![]() ${\dot {b}}$
. We define
${\dot {b}}$
. We define
![]() $u^{\dot {b}}$
in
$u^{\dot {b}}$
in
![]() $\mathbf {V}^{P_{\gamma }} $
such that for every
$\mathbf {V}^{P_{\gamma }} $
such that for every
![]() $l\in {\dot {b}}$
and
$l\in {\dot {b}}$
and
![]() $t\in \,^l2\cap u^{\dot {b}}$
the following hold:
$t\in \,^l2\cap u^{\dot {b}}$
the following hold:
-
• if
 $t\not \in T(\bar Z) t\,^\smallfrown \, 0\in u^{\dot {b}}$
;
$t\not \in T(\bar Z) t\,^\smallfrown \, 0\in u^{\dot {b}}$
; -
• if
 $t \in T(\bar Z) $
let
$t \in T(\bar Z) $
let
 $t\,^\smallfrown \, i\in u^{\dot {b}}$
such that
$t\,^\smallfrown \, i\in u^{\dot {b}}$
such that
 $t\,^\smallfrown \, i\not \in T(\bar Z)$
.
$t\,^\smallfrown \, i\not \in T(\bar Z)$
.
This completes the definition of
![]() $C^{\gamma } (T(\bar Z))=\langle u^{\dot {b}}: {\dot {b}}\in \Omega ^{\gamma }(T(\bar Z))\rangle $
.
$C^{\gamma } (T(\bar Z))=\langle u^{\dot {b}}: {\dot {b}}\in \Omega ^{\gamma }(T(\bar Z))\rangle $
.
Finally, we define a coding system
![]() $C(T(\bar Z))$
in
$C(T(\bar Z))$
in
![]() $\mathbf {V}^{P_{\omega _2} }$
as
$\mathbf {V}^{P_{\omega _2} }$
as
The following main lemma shows that the coding system constructed in Definition 5.1 has the desired property.
Lemma 5.2. If
![]() $T(\bar Z)$
,
$T(\bar Z)$
,
![]() $\mathcal {K}$
and
$\mathcal {K}$
and
![]() $C(T(\bar Z))$
are as in Definition 5.1,
$C(T(\bar Z))$
are as in Definition 5.1,
![]() $\dot x'\in \mathcal {K}$
is arbitrary and
$\dot x'\in \mathcal {K}$
is arbitrary and
![]() $\bar S'$
is the associated fusion with limit
$\bar S'$
is the associated fusion with limit
![]() $p_\omega '$
, then
$p_\omega '$
, then
Proof. Let
![]() $q\leq p_\omega '$
,
$q\leq p_\omega '$
,
![]() $\gamma <\omega _2$
and
$\gamma <\omega _2$
and
![]() $\dot {b}$
be arbitrary such that
$\dot {b}$
be arbitrary such that
We have to find
![]() $q'\leq q$
such that
$q'\leq q$
such that
![]() $q'\Vdash _{P_{\omega _2}}\; \dot {x}'\not \in \left [ u^{\dot {b}}\right ] $
.
$q'\Vdash _{P_{\omega _2}}\; \dot {x}'\not \in \left [ u^{\dot {b}}\right ] $
.
Wlog we may assume that q forces that t is a split node of
![]() $T(\bar {Z})$
whenever
$T(\bar {Z})$
whenever
![]() $\vert t\vert \in \dot {b}$
and t is a possible initial segment of
$\vert t\vert \in \dot {b}$
and t is a possible initial segment of
![]() $\dot {x} '$
below condition q, as otherwise, by the definition of
$\dot {x} '$
below condition q, as otherwise, by the definition of
![]() $u^{\dot {b}} $
, some
$u^{\dot {b}} $
, some
![]() $q'\leq q$
clearly forces that
$q'\leq q$
clearly forces that
![]() $\dot {x}'\upharpoonright \vert t\vert +1\not \in u^{\dot {b}} $
. It follows that we can ignore Case III.
$\dot {x}'\upharpoonright \vert t\vert +1\not \in u^{\dot {b}} $
. It follows that we can ignore Case III.
We need to consider the different cases in Definition 5.1.
Case I:
Wlog we may assume that
![]() $q\Vdash _{P_{\omega _2}} \dot {b}\subseteq L(\beta )$
, for some
$q\Vdash _{P_{\omega _2}} \dot {b}\subseteq L(\beta )$
, for some
![]() $\beta \in Y$
, hence we have
$\beta \in Y$
, hence we have
![]() $\pi '(\beta )\in \mathrm {supp}(p_\omega ')$
and in
$\pi '(\beta )\in \mathrm {supp}(p_\omega ')$
and in
![]() $\mathbf {V}^{P_{\gamma }}$
we have fixed the partition
$\mathbf {V}^{P_{\gamma }}$
we have fixed the partition
![]() $\dot {b}=\dot {b}_0\cup \dot {b}_1 $
for the definition of
$\dot {b}=\dot {b}_0\cup \dot {b}_1 $
for the definition of
![]() $u^{\dot {b}}$
.
$u^{\dot {b}}$
.
Let
![]() $G_{\gamma +1}$
be a
$G_{\gamma +1}$
be a
![]() $P_{\gamma +1} $
-generic filter containing
$P_{\gamma +1} $
-generic filter containing
![]() $q\upharpoonright \gamma +1 $
. Moreover, we let
$q\upharpoonright \gamma +1 $
. Moreover, we let
![]() $b=\dot {b}[G_{\gamma }]$
and
$b=\dot {b}[G_{\gamma }]$
and
![]() $b_i=\dot {b}_i[G_{\gamma }]$
for
$b_i=\dot {b}_i[G_{\gamma }]$
for
![]() $i<2$
.
$i<2$
.
Subcase I(0): We have
![]() $\pi '(\beta )\geq \gamma $
. We can proceed essentially as in the first case of the proof of Lemma 4.1 with
$\pi '(\beta )\geq \gamma $
. We can proceed essentially as in the first case of the proof of Lemma 4.1 with
![]() ${b}_0$
in place of b, as
${b}_0$
in place of b, as
![]() $\dot {g}_{\pi '(\beta )}$
is generic over
$\dot {g}_{\pi '(\beta )}$
is generic over
![]() $\mathbf {V}[G_{\gamma }]$
, where we have defined the levels from
$\mathbf {V}[G_{\gamma }]$
, where we have defined the levels from
![]() ${b}_0$
of
${b}_0$
of
![]() $u^{{b}}$
.
$u^{{b}}$
.
In
![]() $ \mathbf {V}\left [ G_{\gamma }\right ] $
, we obtain the partial evaluations
$ \mathbf {V}\left [ G_{\gamma }\right ] $
, we obtain the partial evaluations
![]() $T^q\left [ G_{\gamma } \right ] $
and
$T^q\left [ G_{\gamma } \right ] $
and
![]() $R^q\left [ G_{\gamma } \right ] $
of the trees
$R^q\left [ G_{\gamma } \right ] $
of the trees
![]() $T^q=T^q(\dot {x}')$
and
$T^q=T^q(\dot {x}')$
and
![]() $R^q=R^q(\dot {x}')$
defined accordingly for
$R^q=R^q(\dot {x}')$
defined accordingly for
![]() $\dot {x} '$
and
$\dot {x} '$
and
![]() $q$
as in the proof of Lemma 4.1, i.e.,:
$q$
as in the proof of Lemma 4.1, i.e.,:
and
![]() $T^q\left [ G_{\gamma }\right ]$
is the subtree of
$T^q\left [ G_{\gamma }\right ]$
is the subtree of
![]() $T^q$
generated by all
$T^q$
generated by all
![]() $t_s\in T^q$
where
$t_s\in T^q$
where
![]() $s\in R^q [ G_{\gamma } ]$
.
$s\in R^q [ G_{\gamma } ]$
.
Wlog we may assume that in
![]() $ \mathbf {V}\left [ G_{\gamma }\right ] $
there are
$ \mathbf {V}\left [ G_{\gamma }\right ] $
there are
![]() $k, v,m_0,n_0,l,n_1,m_1$
such that
$k, v,m_0,n_0,l,n_1,m_1$
such that
![]() $q\upharpoonright \pi '(\beta ) $
forces (with respect to the forcing
$q\upharpoonright \pi '(\beta ) $
forces (with respect to the forcing
![]() $P_{\omega _2}/G_{\gamma } $
) the following:
$P_{\omega _2}/G_{\gamma } $
) the following:
-
•
 $v\in \, ^k2$
, stem
$v\in \, ^k2$
, stem
 $(q(\pi '(\beta )))=\,\mathrm {stem}(p_\omega '(\pi '(\beta ))^v)$
and
$(q(\pi '(\beta )))=\,\mathrm {stem}(p_\omega '(\pi '(\beta ))^v)$
and
 $m_0=\vert \mathrm {stem}(q(\pi '(\beta )))\vert $
;
$m_0=\vert \mathrm {stem}(q(\pi '(\beta )))\vert $
; -
• at step
 $n_0$
of the fusion
$n_0$
of the fusion
 $\bar {S}'$
that produced
$\bar {S}'$
that produced
 $p_\omega '$
,
$p_\omega '$
,
 $\pi '(\beta )$
was active for the kth time;
$\pi '(\beta )$
was active for the kth time; -
•
 $l\in b_0$
is bigger than
$l\in b_0$
is bigger than
 $\max \left \lbrace \vert t_s\vert : s\in \,^{n_0}2\right \rbrace $
;
$\max \left \lbrace \vert t_s\vert : s\in \,^{n_0}2\right \rbrace $
; -
•
 $n_1\in Z(\beta )$
is such that
$n_1\in Z(\beta )$
is such that
 $\forall \,t\in T^q\left [ G_{\gamma }\right ] \cap \,^l2\,\exists \,s\in R^q\left [ G_{\gamma }\right ] \cap \, ^{n_1}2\quad t=t_s$
;
$\forall \,t\in T^q\left [ G_{\gamma }\right ] \cap \,^l2\,\exists \,s\in R^q\left [ G_{\gamma }\right ] \cap \, ^{n_1}2\quad t=t_s$
; -
•
 $\dot {c}(p_\omega ', \pi '(\beta ))(n_1) =m_1,$
and
$\dot {c}(p_\omega ', \pi '(\beta ))(n_1) =m_1,$
and -
• for every
 $s\in R^q\left [ G_{\gamma }\right ] $
with
$s\in R^q\left [ G_{\gamma }\right ] $
with
 $\vert s\vert =n_1$
, we have
$\vert s\vert =n_1$
, we have  $$ \begin{align*}q\left[ G_{\gamma}\right] \wedge a^s(\bar{S} ')\left[ G_{\gamma}\right]\;\Vdash_{P_{\omega_2}/G_{\gamma}} \, \dot{x}'(\vert t_s\vert)=t_{s\,^ \smallfrown \, \dot{g}_{\pi'(\beta)} (m_1)}( \vert t_s\vert).\end{align*} $$
$$ \begin{align*}q\left[ G_{\gamma}\right] \wedge a^s(\bar{S} ')\left[ G_{\gamma}\right]\;\Vdash_{P_{\omega_2}/G_{\gamma}} \, \dot{x}'(\vert t_s\vert)=t_{s\,^ \smallfrown \, \dot{g}_{\pi'(\beta)} (m_1)}( \vert t_s\vert).\end{align*} $$
Analogously as in the proof of Lemma 4.1, in
![]() $\mathbf {V}$
we find
$\mathbf {V}$
we find
![]() $\hat {q}\leq q $
in
$\hat {q}\leq q $
in
![]() $P_{\omega _2}$
such that
$P_{\omega _2}$
such that
![]() $\hat q\upharpoonright \pi '(\beta )$
forces all these facts and
$\hat q\upharpoonright \pi '(\beta )$
forces all these facts and
![]() $\hat q\upharpoonright \pi '(\beta )$
also decides
$\hat q\upharpoonright \pi '(\beta )$
also decides
![]() $k,v,m_0,n_0,l, n_1,m_1$
as above. Moreover,
$k,v,m_0,n_0,l, n_1,m_1$
as above. Moreover,
and
![]() $\hat q\upharpoonright \pi '(\beta )$
decides
$\hat q\upharpoonright \pi '(\beta )$
decides
![]() $\hat {q}(\pi '(\beta ))\upharpoonright m_1+1$
, thus
$\hat {q}(\pi '(\beta ))\upharpoonright m_1+1$
, thus
![]() $\dot g_{\pi '(\beta )} \upharpoonright (m_1+1 \setminus \lbrace m_0\rbrace ) $
, say as
$\dot g_{\pi '(\beta )} \upharpoonright (m_1+1 \setminus \lbrace m_0\rbrace ) $
, say as
![]() $\langle g(0),...,g(m_0 -1),g(m_0 +1),...,g(m_1)\rangle $
.
$\langle g(0),...,g(m_0 -1),g(m_0 +1),...,g(m_1)\rangle $
.
Now we can find
![]() $s_0,s_1\in R^{\hat {q}}\cap \, ^{n_1} 2$
such that
$s_0,s_1\in R^{\hat {q}}\cap \, ^{n_1} 2$
such that
![]() $s_i(n_0)=i$
and
$s_i(n_0)=i$
and
![]() $s_0(j) =s_1(j)$
for every
$s_0(j) =s_1(j)$
for every
![]() $j\in Z(\beta )\cap n_1\setminus \left \lbrace n_0\right \rbrace $
, and hence
$j\in Z(\beta )\cap n_1\setminus \left \lbrace n_0\right \rbrace $
, and hence
We know that both
![]() $t_{s_0}$
and
$t_{s_0}$
and
![]() $t_{s_1}$
are splitnodes of
$t_{s_1}$
are splitnodes of
![]() $T(\bar {Z})$
of length l. We can choose j such that
$T(\bar {Z})$
of length l. We can choose j such that
![]() $i(t_{s_j\,^\smallfrown \,g(m_1)},\beta ) \ne g(m_1)$
and a common extension
$i(t_{s_j\,^\smallfrown \,g(m_1)},\beta ) \ne g(m_1)$
and a common extension
![]() $q'$
of
$q'$
of
![]() $\hat {q}$
and
$\hat {q}$
and
![]() $a^{s_j}(\bar {S}' ) $
. We conclude
$a^{s_j}(\bar {S}' ) $
. We conclude
and hence
![]() $q'\Vdash _{P_{\omega _2}}\; \dot x'\not \in \left [ u^{\dot {b}}\right ],$
by the definition of
$q'\Vdash _{P_{\omega _2}}\; \dot x'\not \in \left [ u^{\dot {b}}\right ],$
by the definition of
![]() $u^{\dot {b}}$
.
$u^{\dot {b}}$
.
Subcase I(1): We have
![]() $\pi ' (\beta )<\gamma $
. In the intermediate model
$\pi ' (\beta )<\gamma $
. In the intermediate model
![]() $\mathbf {V}[G_\gamma ]$
we have the restricted tree of possibilities for
$\mathbf {V}[G_\gamma ]$
we have the restricted tree of possibilities for
![]() $\dot {x} '$
,
$\dot {x} '$
,
![]() $T^q(\dot {x}')[G_\gamma ]$
(which is analogously defined as in Subcase I(0) above). We know that every
$T^q(\dot {x}')[G_\gamma ]$
(which is analogously defined as in Subcase I(0) above). We know that every
is a splitnode of
![]() $T(\bar {Z})$
, hence
$T(\bar {Z})$
, hence
![]() $t=t_s$
for some
$t=t_s$
for some
Now we have that if
![]() $l\in L(\beta )$
,
$l\in L(\beta )$
,
![]() $t\in T^q(\dot {x}')[G_\gamma ]$
,
$t\in T^q(\dot {x}')[G_\gamma ]$
,
![]() $\vert t\vert =l$
and
$\vert t\vert =l$
and
![]() $t=t_s$
, then
$t=t_s$
, then
![]() $t_s$
is no longer a splitnode of
$t_s$
is no longer a splitnode of
![]() $T^q(\dot {x}')[G_\gamma ]$
, and its successive digit is
$T^q(\dot {x}')[G_\gamma ]$
, and its successive digit is
If in addition
![]() $l\in b_1$
, we have
$l\in b_1$
, we have
![]() $\vert s\vert \in Z(b_1)$
. Note that by property (i) of a coding tree,
$\vert s\vert \in Z(b_1)$
. Note that by property (i) of a coding tree,
![]() $\vert s\vert $
does not depend on t (but on l of course).
$\vert s\vert $
does not depend on t (but on l of course).
Hence in
![]() $\mathbf {V}[G_{\gamma }]$
we can define a function
$\mathbf {V}[G_{\gamma }]$
we can define a function
![]() $F=F(\dot {x}'):Z(b_1)\rightarrow 2$
as follows: Given
$F=F(\dot {x}'):Z(b_1)\rightarrow 2$
as follows: Given
![]() $i\in Z(b_1)$
, we let
$i\in Z(b_1)$
, we let
For the definition of
![]() $u^b$
on levels in
$u^b$
on levels in
![]() $b_1$
in the present case we applied some new function
$b_1$
in the present case we applied some new function
![]() $h=\dot {h}[G_{\gamma +1}]\in \mathbf {V}\left [ G_{\gamma +1}\right ]\setminus \mathbf {V}\left [ G_{\gamma }\right ]$
,
$h=\dot {h}[G_{\gamma +1}]\in \mathbf {V}\left [ G_{\gamma +1}\right ]\setminus \mathbf {V}\left [ G_{\gamma }\right ]$
,
![]() $h:Z(b_1)\rightarrow 2$
. Hence clearly we have
$h:Z(b_1)\rightarrow 2$
. Hence clearly we have
By construction we can find s with
![]() $\vert s\vert =i$
,
$\vert s\vert =i$
,
![]() $i\in Z(b_1)$
,
$i\in Z(b_1)$
,
![]() $h(i)\ne F(i)$
and
$h(i)\ne F(i)$
and
![]() $t_s\in T^q(\dot {x}')[G_\gamma ]$
. Letting
$t_s\in T^q(\dot {x}')[G_\gamma ]$
. Letting
![]() $l=\vert t_s\vert $
, hence
$l=\vert t_s\vert $
, hence
![]() $l\in b_1$
, we get that
$l\in b_1$
, we get that
Hence, as
![]() $t_{s\,^{\smallfrown } F(i)} \in T^q(\dot {x}')[G_\gamma ]$
, there exists
$t_{s\,^{\smallfrown } F(i)} \in T^q(\dot {x}')[G_\gamma ]$
, there exists
![]() $q'\leq q$
in
$q'\leq q$
in
![]() $P_{\omega _2}$
(with
$P_{\omega _2}$
(with
![]() $q'\upharpoonright \gamma \in G_\gamma $
) such that
$q'\upharpoonright \gamma \in G_\gamma $
) such that
and therefore, by the definition of
![]() $u^{\dot {b}}$
on levels in
$u^{\dot {b}}$
on levels in
![]() $\dot {b}_1$
, we conclude
$\dot {b}_1$
, we conclude
Note that the proof here, in particular the correct choice of s that leads to a contradiction, is quite subtle. On the one hand we have that for every
![]() $t\in T^q(\dot {x}')[G_\gamma ]$
such that
$t\in T^q(\dot {x}')[G_\gamma ]$
such that
![]() $t=t_{s'}$
for some
$t=t_{s'}$
for some
![]() $s'$
of same length as s we have
$s'$
of same length as s we have
Note that this does not imply that, letting
![]() $l=\vert t_s\vert $
and
$l=\vert t_s\vert $
and
![]() $l'=\vert t_{s'} \vert $
,
$l'=\vert t_{s'} \vert $
,
(which is generally false). On the other hand, such other
![]() $s'$
might be useless for our purpose as not necessarily
$s'$
might be useless for our purpose as not necessarily
![]() $\vert t_{s'}\vert \in b_1$
(see the remark after the the definition of
$\vert t_{s'}\vert \in b_1$
(see the remark after the the definition of
![]() $Z(b)$
at the beginning of Definition 5.1).
$Z(b)$
at the beginning of Definition 5.1).
Case II:
Let
![]() $\dot {b}\in \Omega ^{\gamma }(T(\bar Z))$
,
$\dot {b}\in \Omega ^{\gamma }(T(\bar Z))$
,
![]() $\dot \delta $
and
$\dot \delta $
and
![]() $\dot {b}_0,\dot {b}_1\subseteq \dot {b}$
be as there, and let
$\dot {b}_0,\dot {b}_1\subseteq \dot {b}$
be as there, and let
![]() $G_{\gamma +1}$
be a
$G_{\gamma +1}$
be a
![]() $P_{\gamma +1}$
-generic filter containing
$P_{\gamma +1}$
-generic filter containing
![]() $q\upharpoonright \gamma +1$
. Let
$q\upharpoonright \gamma +1$
. Let
![]() $b,\delta , b_0,b_1$
be the evaluations of
$b,\delta , b_0,b_1$
be the evaluations of
![]() $\dot {b}_0,\dot {b}_1,\dot {b}$
by
$\dot {b}_0,\dot {b}_1,\dot {b}$
by
![]() $G_{\gamma }$
, respectively.
$G_{\gamma }$
, respectively.
Subcase II(0): We have
![]() $\sup (\pi '[Y(b_0)])>\gamma $
. We proceed essentially as in the second case in the proof of Lemma 4.1. We argue in
$\sup (\pi '[Y(b_0)])>\gamma $
. We proceed essentially as in the second case in the proof of Lemma 4.1. We argue in
![]() $\mathbf {V} [G_{\gamma }]$
. The set
$\mathbf {V} [G_{\gamma }]$
. The set
is infinite, so we can find a large enough
![]() $\beta \in Y(b_0)$
,
$\beta \in Y(b_0)$
,
![]() $l\in b_0\cap L(\beta )$
,
$l\in b_0\cap L(\beta )$
,
![]() $n\in Z(\beta )$
and
$n\in Z(\beta )$
and
![]() $s\in \, ^n2$
,
$s\in \, ^n2$
,
![]() $s_0,s_1\in \,^n2 \cap R^q(\dot {x}')[G_{\gamma }]$
such that
$s_0,s_1\in \,^n2 \cap R^q(\dot {x}')[G_{\gamma }]$
such that
![]() $\vert t_s \vert =l$
and
$\vert t_s \vert =l$
and
As in the proof of Lemma 4.1 we can apply properties (i) and (ii) of the coding tree
![]() $T(\bar Z)$
to find
$T(\bar Z)$
to find
![]() $q'\leq q$
,
$q'\leq q$
,
![]() $j<2$
and
$j<2$
and
![]() $t\in \,^l2$
compatible with
$t\in \,^l2$
compatible with
![]() $t_{s_j}$
such that t is not a splitnode of
$t_{s_j}$
such that t is not a splitnode of
![]() $T(\bar Z)$
and
$T(\bar Z)$
and
and hence
Subcase II(1): This is similar to Subcase I(1). We have
![]() $\sup (\pi ' [Y(b_0)])\leq \gamma $
. In the intermediate model
$\sup (\pi ' [Y(b_0)])\leq \gamma $
. In the intermediate model
![]() $\mathbf {V}[G_\gamma ]$
we have the restricted tree of possibilities for
$\mathbf {V}[G_\gamma ]$
we have the restricted tree of possibilities for
![]() $\dot {x} '$
,
$\dot {x} '$
,
![]() $T^q(\dot {x}')[G_\gamma ]$
(which is analogously defined as in Subcase I(0) above). We know that every
$T^q(\dot {x}')[G_\gamma ]$
(which is analogously defined as in Subcase I(0) above). We know that every
![]() $t\in T^q(\dot {x}')[G_\gamma ] \cap \,\bigcup \left \lbrace \,^l 2: l\in b_1\right \rbrace $
is a splitnode of
$t\in T^q(\dot {x}')[G_\gamma ] \cap \,\bigcup \left \lbrace \,^l 2: l\in b_1\right \rbrace $
is a splitnode of
![]() $T(\bar {Z})$
, hence
$T(\bar {Z})$
, hence
![]() $t=t_s$
for some
$t=t_s$
for some
![]() $s\in \bigcup \left \lbrace \,^{i}2: i\in {Z(b_1)}\right \rbrace $
.
$s\in \bigcup \left \lbrace \,^{i}2: i\in {Z(b_1)}\right \rbrace $
.
Now we have that if
![]() $\beta \in \mathrm {dom}(p_\omega )$
,
$\beta \in \mathrm {dom}(p_\omega )$
,
![]() $\beta '=\pi '(\beta )<\gamma $
,
$\beta '=\pi '(\beta )<\gamma $
,
![]() $l\in L(\beta )$
,
$l\in L(\beta )$
,
![]() $t\in T^q(\dot {x}')[G_\gamma ]$
,
$t\in T^q(\dot {x}')[G_\gamma ]$
,
![]() $\vert t\vert =l$
and
$\vert t\vert =l$
and
![]() $t=t_s$
, then
$t=t_s$
, then
![]() $t_s$
is no longer a splitnode of
$t_s$
is no longer a splitnode of
![]() $T^q(\dot {x}')[G_\gamma ]$
, and its successive digit is
$T^q(\dot {x}')[G_\gamma ]$
, and its successive digit is
If in addition
![]() $l\in b_1$
, we have
$l\in b_1$
, we have
![]() $\vert s\vert \in Z(b_1)$
.
$\vert s\vert \in Z(b_1)$
.
By what we noticed so far, in
![]() $\mathbf {V}[G_{\gamma }]$
we can define a function
$\mathbf {V}[G_{\gamma }]$
we can define a function
![]() $F=F(\dot {x}'):Z(b_1)\rightarrow 2$
as follows: Given
$F=F(\dot {x}'):Z(b_1)\rightarrow 2$
as follows: Given
![]() $i\in Z(b_1)$
, letting
$i\in Z(b_1)$
, letting
![]() $\beta '\in \mathrm {supp}(p_\omega ')$
with
$\beta '\in \mathrm {supp}(p_\omega ')$
with
![]() $i\in Z(\beta ')$
, we let
$i\in Z(\beta ')$
, we let
As
![]() $h\ne F$
(
$h\ne F$
(
![]() $h=\dot {h}[G_{\gamma +1}]$
where
$h=\dot {h}[G_{\gamma +1}]$
where
![]() $\dot {h}$
is from the Definition 5.1(II)(1)) there is
$\dot {h}$
is from the Definition 5.1(II)(1)) there is
![]() $i\in Z(b_1)$
such that
$i\in Z(b_1)$
such that
![]() $h(i)\ne F(i)$
. By construction we can find s and
$h(i)\ne F(i)$
. By construction we can find s and
![]() $\beta '$
with
$\beta '$
with
![]() $\vert s\vert =i$
and
$\vert s\vert =i$
and
![]() $i\in Z(\beta ')$
such that
$i\in Z(\beta ')$
such that
![]() $\vert t_s\vert \in b_1$
and
$\vert t_s\vert \in b_1$
and
![]() $t_s\in T^q(\dot {x}')[G_\gamma ]$
. We get that
$t_s\in T^q(\dot {x}')[G_\gamma ]$
. We get that
Hence, letting
![]() $l:=\vert t_s\vert $
, as
$l:=\vert t_s\vert $
, as
![]() $t_{s\,^{\smallfrown } F(i)} \in T^q(\dot {x}')[G_\gamma ]$
there exists
$t_{s\,^{\smallfrown } F(i)} \in T^q(\dot {x}')[G_\gamma ]$
there exists
![]() $q'\leq q$
in
$q'\leq q$
in
![]() $P_{\omega _2}$
(with
$P_{\omega _2}$
(with
![]() $q'\upharpoonright \gamma \in G_\gamma $
) such that
$q'\upharpoonright \gamma \in G_\gamma $
) such that
and therefore, by the definition of
![]() $u^{\dot {b}}$
on levels in
$u^{\dot {b}}$
on levels in
![]() $\dot {b}_1$
, we conclude
$\dot {b}_1$
, we conclude
Case III:
In this case we have that no splitnode of
![]() $T(\bar Z)$
has its length in
$T(\bar Z)$
has its length in
![]() $\dot {b}$
, and therefore, as we have noticed already,
$\dot {b}$
, and therefore, as we have noticed already,
follows immediately by the definition of
![]() $u^b$
.
$u^b$
.
We have completed the proof of Lemma 5.2.
6 Conclusion
By Lemma 5.2 we obtain our main result.
Theorem 6.1. If
![]() $\mathbf {V}\models \mathrm {ZFC+CH}$
and
$\mathbf {V}\models \mathrm {ZFC+CH}$
and
![]() $P_{\omega _2}$
is the CS-iteration of Silver forcing
$P_{\omega _2}$
is the CS-iteration of Silver forcing
![]() $\mathbb {SI}$
of length
$\mathbb {SI}$
of length
![]() $\omega _2$
, then
$\omega _2$
, then
Proof. Given any
![]() $P_{\omega _2}$
-name
$P_{\omega _2}$
-name
![]() $\dot x$
and
$\dot x$
and
![]() $p\in P_{\omega _2}$
such that
$p\in P_{\omega _2}$
such that
by Theorem 3.1 we obtain a fusion sequence
![]() $\bar {S}$
with limit
$\bar {S}$
with limit
![]() $p_\omega \leq p$
and a tree
$p_\omega \leq p$
and a tree
![]() $T=T(\dot x, \bar S)$
with properties (0), (1), and (2), which is the tree of possibilities of
$T=T(\dot x, \bar S)$
with properties (0), (1), and (2), which is the tree of possibilities of
![]() $\dot x$
below
$\dot x$
below
![]() $p_\omega $
. Let
$p_\omega $
. Let
![]() $\mathcal {K}$
be the isomorphism type of
$\mathcal {K}$
be the isomorphism type of
![]() $\dot x$
as defined in Definition 4.2. Moreover, every
$\dot x$
as defined in Definition 4.2. Moreover, every
![]() $\dot x'\in \mathcal {K}$
produces the same tree.
$\dot x'\in \mathcal {K}$
produces the same tree.
In Definition 4.1 we have defined a coding system
![]() $C^0(T)=\langle u^b: b\in \Omega ^0\rangle $
depending only on
$C^0(T)=\langle u^b: b\in \Omega ^0\rangle $
depending only on
![]() $\mathcal {K}$
such that, by Lemma 4.1, in
$\mathcal {K}$
such that, by Lemma 4.1, in
![]() $\mathbf {V}$
$\mathbf {V}$
In Definition 5.1, for every
![]() $0<\gamma <\omega _2$
of countable cofinality we have defined a coding system
$0<\gamma <\omega _2$
of countable cofinality we have defined a coding system
![]() $C^{\gamma }(T)=\langle u^b:b\in \Omega ^{\gamma }(T)\rangle $
in
$C^{\gamma }(T)=\langle u^b:b\in \Omega ^{\gamma }(T)\rangle $
in
![]() $\mathbf {V}^{P_{\gamma +1}}$
, where
$\mathbf {V}^{P_{\gamma +1}}$
, where
![]() $\Omega ^{\gamma }(T)\subseteq \left [ \omega \right ] ^\omega $
is dense in
$\Omega ^{\gamma }(T)\subseteq \left [ \omega \right ] ^\omega $
is dense in
![]() $\mathbf {V}^{P_\gamma }$
with
$\mathbf {V}^{P_\gamma }$
with
![]() $\Omega ^{\gamma }(T)\cap \bigcup _{\beta <\gamma }\mathbf {V}^{P_\beta }=\emptyset $
, such that by Lemma 5.2 we have
$\Omega ^{\gamma }(T)\cap \bigcup _{\beta <\gamma }\mathbf {V}^{P_\beta }=\emptyset $
, such that by Lemma 5.2 we have
For
![]() $\gamma <\omega _2$
of uncountable cofinality,
$\gamma <\omega _2$
of uncountable cofinality,
![]() $\Omega ^{\gamma }(T)$
and
$\Omega ^{\gamma }(T)$
and
![]() $C^{\gamma }(T)$
were defined by taking the union of the
$C^{\gamma }(T)$
were defined by taking the union of the
![]() $\Omega ^{\beta }(T)$
,
$\Omega ^{\beta }(T)$
,
![]() $C^{\beta }(T)$
, respectively, for
$C^{\beta }(T)$
, respectively, for
![]() $\beta <\gamma $
. Hence in
$\beta <\gamma $
. Hence in
![]() $\mathbf {V}^{P_{\omega _2}}$
we have the
$\mathbf {V}^{P_{\omega _2}}$
we have the
![]() $\mathfrak {C}_2$
-set
$\mathfrak {C}_2$
-set
![]() $A(C)$
, where
$A(C)$
, where
![]() $C=\langle u^b:b\in \Omega ^{\gamma }, \gamma <\omega _2\rangle $
, such that
$C=\langle u^b:b\in \Omega ^{\gamma }, \gamma <\omega _2\rangle $
, such that
As
![]() $A(C)$
only depends on T, and as by CH in the ground model there are only
$A(C)$
only depends on T, and as by CH in the ground model there are only
![]() $\aleph _1$
-many isomorphism types
$\aleph _1$
-many isomorphism types
![]() $\mathcal {K}$
, we have proved that in
$\mathcal {K}$
, we have proved that in
![]() $\mathbf {V}^{P_{\omega _2}}$
,
$\mathbf {V}^{P_{\omega _2}}$
,
![]() $^\omega 2\setminus \mathbf {V}$
can be covered by
$^\omega 2\setminus \mathbf {V}$
can be covered by
![]() $\aleph _1$
-many
$\aleph _1$
-many
![]() $\mathfrak {C}_2$
-sets. By Corollary 5.1(2) we know that
$\mathfrak {C}_2$
-sets. By Corollary 5.1(2) we know that
![]() $^\omega 2\cap \mathbf {V}$
is even in
$^\omega 2\cap \mathbf {V}$
is even in
![]() $\mathfrak {P}_2$
. Hence cov
$\mathfrak {P}_2$
. Hence cov
![]() $(\mathfrak {C}_2)=\aleph _1$
holds in
$(\mathfrak {C}_2)=\aleph _1$
holds in
![]() $\mathbf {V}^{P_{\omega _2}}$
.
$\mathbf {V}^{P_{\omega _2}}$
.
As we have explained in the introduction,
![]() $\mathbf {V}^{P_{\omega _2}}\models \;\mathrm {cov}(v^0)=\aleph _2$
, where
$\mathbf {V}^{P_{\omega _2}}\models \;\mathrm {cov}(v^0)=\aleph _2$
, where
![]() $v^0$
is the Silver ideal. As
$v^0$
is the Silver ideal. As
![]() $\mathfrak {P}_2\subseteq v^0$
, we have
$\mathfrak {P}_2\subseteq v^0$
, we have
![]() $\mathbf {V}^{P_{\omega _2}}\models \;\mathrm {cov}(\mathfrak {P}_2)=\aleph _2$
.
$\mathbf {V}^{P_{\omega _2}}\models \;\mathrm {cov}(\mathfrak {P}_2)=\aleph _2$
.
Acknowledgments
I would like to thank Martin Goldstern for bringing Grigorieff’s paper to my attention. Moreover, I am indebted to the referee for his several very careful and sharp reports which forced me to clear up several obscure or faulty arguments.
Funding
The author would like to thank the DFG for partial support (Grant No. SP683/5-1).