Article contents
Countable models of multidimensional ℵ0-stable theories
Published online by Cambridge University Press: 12 March 2014
Extract
The notations and the definitions used here are identical to those in [B.L.]. We also assume that the reader is familiar with the properties of the Rudin-Keisler order on types [L.].
Let T denote an ℵ0-stable countable theory. The main result in [B.L.] is: All countable models of T are almost homogeneous if and only if T satisfies
(*) For all models M of T and all ā ∈ M, if p ∈ S1(ā) is strongly regular multidimensional, then Dim(p; M) ≥ ℵ0.
In this paper we investigate the case of a theory T which does not satisfy condition (*) and, under certain additional assumptions, we construct 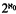 nonisomorphic and non-almost-homogeneous countable models. The same type of construction has been used before to show that if T is multidimensional, then for all α ≥ 1, T has at least
nonisomorphic and non-almost-homogeneous countable models. The same type of construction has been used before to show that if T is multidimensional, then for all α ≥ 1, T has at least 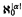 nonisomorphic models of cardinality ℵα [La.], [Sh.]. As a corollary of our main theorem (Theorem 6) and of the previous result in [B.L.], we prove Vaught's Conjecture (and, in fact, Martin's Strong Conjecture) for theories T with αT finite.
nonisomorphic models of cardinality ℵα [La.], [Sh.]. As a corollary of our main theorem (Theorem 6) and of the previous result in [B.L.], we prove Vaught's Conjecture (and, in fact, Martin's Strong Conjecture) for theories T with αT finite.
Although we are here interested in countable models, we can also note that our construction proves that theories satisfying the assumptions in Theorem 6 have at least 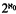 nonisomorphic models of cardinality ℵα.
nonisomorphic models of cardinality ℵα.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1983
References
REFERENCES
- 5
- Cited by


