Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-22T21:02:52.811Z Has data issue: false hasContentIssue false
  • English
  • Français

The cost of a cycle is a square

Published online by Cambridge University Press:  12 March 2014

A. Carbone
A. Carbone*
Affiliation:
Mathématiques/Informatique, Université de Paris XII, 61 Avenue Du Général De Gaulle, 94010 Créteil Cedex, France, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The logical flow graphs of sequent calculus proofs might contain oriented cycles. For the predicate calculus the elimination of cycles might be non-elementary and this was shown in [Car96]. For the propositional calculus, we prove that if a proof of k lines contains n cycles then there exists an acyclic proof with 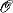(kn+1) lines. In particular, there is a polynomial time algorithm which eliminates cycles from a proof. These results are motivated by the search for general methods on proving lower bounds on proof size and by the design of more efficient heuristic algorithms for proof search.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 67 , Issue 1 , March 2002 , pp. 35 - 60
Copyright
Copyright © Association for Symbolic Logic 2002

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[Bus91]Buss, S., The undecidability of k-provability, Annals of Pure and Applied Logic, vol. 53 (1991), pp. 72–102.CrossRefGoogle Scholar
[Bus95]Buss, S., Some remarks on lengths of propositional proofs, Archive for Mathematical Logic, vol. 34 (1995), pp. 377–394.CrossRefGoogle Scholar
[Bus93]Buss, S., Personal communication, 06 1993.Google Scholar
[Car97]Carbone, A., Interpolants, cut elimination and flow graphs for the propositional calculus, Annals of Pure and Applied Logic, vol. 83 (1997), pp. 249–299.CrossRefGoogle Scholar
[Car97b]Carbone, A., Duplication of directed graphs and exponential blow up of proofs, Annals of Pure and Applied Logic, vol. 100 (1999), pp. 1–76.CrossRefGoogle Scholar
[Car97a]Carbone, A., Turning cycles into spirals, Annals of Pure and Applied Logic, vol. 96 (1999), pp. 57–73.CrossRefGoogle Scholar
[Car96]Carbone, A., Cycling in proofs and feasibility, Transactions of the American Mathematical Society, vol. 352 (2000), pp. 2049–2075.CrossRefGoogle Scholar
[CS97]Carbone, A. and Semmes, S., Making proofs without modus ponens: an introduction to the combinatorics and complexity of cut elimination, Bulletin of the American Mathematical Society, vol. 34 (1997), pp. 131–159.CrossRefGoogle Scholar
[CS97a]Carbone, A. and Semmes, S., A Graphic Apology for Symmetry and Implicitness — Combinatorial Complexity of Proofs, Languages and Geometric Constructions, Mathematical monographs, Oxford University Press, 2000.Google Scholar
[CR79]Cook, S. and Reckhow, R., The relative efficiency of propositional proof systems, this Journal, vol. 44 (1979), pp. 36–50.Google Scholar
[Gen34]Gentzen, Gerhard, Untersuchungen über das logische Schließien I–II, Mathematische Zeitschrift, vol. 39 (1934), pp. 176–210, 405–431.CrossRefGoogle Scholar
[Gir87]Girard, Jean-Yves, Linear logic, Theoretical Computer Science, vol. 50 (1987), pp. 101–102.CrossRefGoogle Scholar
[Gir87a]Girard, Jean-Yves, Proof theory and logical complexity, Volume 1 of Studies in Proof Theory, Monographs, Bibliopolis, Naples, Italy, 1987.Google Scholar
[Hak85]Hakén, A., The intractability of resolution, Theoretical Computer Science, vol. 39 (1985), pp. 297–308.CrossRefGoogle Scholar
[Kra97]Krajíček, J., Interpolation theorems, lower bounds for proof systems, and independence results for bounded arithmetic, this Journal, vol. 62 (1997), no. 2, pp. 457–486.Google Scholar
[Ore79]Orevkov, Vladimir P., Lower bounds for increasing complexity of derivations after cut elimination, Journal of Soviet Mathematics, vol. 20 (1982), no. 4.CrossRefGoogle Scholar
[Ore93]Orevkov, Vladimir P., Complexity of proofs and their transformations in axiomatic theories, Translations of Mathematical Monographs 128, American Mathematical Society, Providence, RI, 1993.Google Scholar
[Pud96]Pudlák, P., The lengths of proofs, Handbook of proof theory (Buss, S., editor), North-Holland, Amsterdam, 1996.Google Scholar
[Pud97]Pudlák, P., Lower bounds for resolution and cutting plane proofs and monotone computations, this Journal, vol. 62 (1997), no. 3, pp. 981–998.Google Scholar
[Sta78]Statman, R., Bounds for proof-search and speed-up in the predicate calculus, Annals of Mathematical Logic, vol. 15 (1978), pp. 225–287.CrossRefGoogle Scholar
[Tak87]Takeuti, G., Proof theory, 2nd ed., Studies in Logic 81, North-Holland, Amsterdam, 1987.Google Scholar
[Tse68]Tseitin, G.S., Complexity of a derivation in the propositional calculus, Zapiski Nauchnykh Seminarov, Leningrad Otdelenie Matematicheskiĭ Institut, Akademiya Nauka SSSR, vol. 8 (1968), pp. 234–259.Google Scholar