Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Schlutzenberg, Farmer
2023.
The definability of E in self-iterable mice.
Annals of Pure and Applied Logic,
Vol. 174,
Issue. 2,
p.
103208.
SCHLUTZENBERG, FARMER
2024.
THE DEFINABILITY OF THE EXTENDER SEQUENCE
$\mathbb {E}$
FROM
$\mathbb {E}\upharpoonright \aleph _1$
IN
$L[\mathbb {E}]$
.
The Journal of Symbolic Logic,
Vol. 89,
Issue. 2,
p.
427.


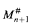 doesn't exist, then the core model
doesn't exist, then the core model 