In this paper a converse of Barwise's completeness theorem is proved by cut-elimination considerations applied to inductive definitions. We show that among the transitive sets T satisfying some weak closure conditions (closure under primitive-recursive set-functions is more than enough), only the unions of admissible sets satisfy Barwise's completeness theorem in the form stating that if φ ∊ T is a sentence which has a derivation (in the universe) then φ has a derivation in T. See §1 for the origin of the problem in Barwise's paper [Ba].

Stated quite briefly the proof is as follows (a step-by-step account including relevant definitions is given in the body of the paper):

Let T be a transitive prim.-rec. closed set, and let 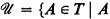is nonempty, transitive and closed under pairs}. For each 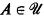let κ(A) be the supremum of closure ordinals of first-order positive operators on subsets of A (first-order with respect to 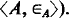By Theorem 1 of [BGM], it is enough to prove that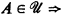 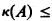rank(T) in order to obtain that T is a union of admissible sets. (The rank of a set is defined by rank(x) = supy ∊ x (rank(y) + 1); since T is prim.-rec. closed, rank(T) = smallest ordinal not in T.)

Let 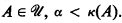We show how to find in T (in fact, in Lω(A)) a derivable sentence τ that has no derivation D such that rank(D) ≤ α. Thus, if τ is to have a derivation in T, rank(T) > α. α is arbitrary (< κ(A)), so rank(T) ≥ κ(A). Q.E.D.