No CrossRef data available.
Published online by Cambridge University Press: 08 June 2021
Fix an abelian group 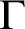 $\Gamma $
and an injective endomorphism
$\Gamma $
and an injective endomorphism 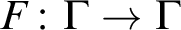 $F\colon \Gamma \to \Gamma $
. Improving on the results of [2], new characterizations are here obtained for the existence of spanning sets, F-automaticity, and F-sparsity. The model theoretic status of these sets is also investigated, culminating with a combinatorial description of the F-sparse sets that are stable in
$F\colon \Gamma \to \Gamma $
. Improving on the results of [2], new characterizations are here obtained for the existence of spanning sets, F-automaticity, and F-sparsity. The model theoretic status of these sets is also investigated, culminating with a combinatorial description of the F-sparse sets that are stable in 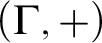 $(\Gamma ,+)$
, and a proof that the expansion of
$(\Gamma ,+)$
, and a proof that the expansion of 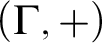 $(\Gamma ,+)$
by any F-sparse set is NIP. These methods are also used to show for prime
$(\Gamma ,+)$
by any F-sparse set is NIP. These methods are also used to show for prime 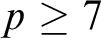 $p\ge 7$
that the expansion of
$p\ge 7$
that the expansion of 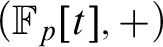 $(\mathbb {F}_p[t],+)$
by multiplication restricted to
$(\mathbb {F}_p[t],+)$
by multiplication restricted to 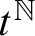 $t^{\mathbb {N}}$
is NIP.
$t^{\mathbb {N}}$
is NIP.