No CrossRef data available.
Published online by Cambridge University Press: 12 March 2014
A computably enumerable Turing degree a is called contiguous iff it contains only a single computably enumerable weak truth table degree (Ladner and Sasso [2]). In [1], the authors proved that a nonzero computably enumerable degree a is contiguous iff it is locally distributive, that is, for all a1, a2, c with a1 ∪a2 = a and c ≤ a, there exist ci, ≤ ai with c1 ∪ c2 = c.
To do this we supposed that W was a computably enumerable set and ∪ a computably set with a Turing functional Φ such that ΦW = U. Then we constructed computably enumerable sets A0, A1 and B together with functionals Γ0, Γ1, Γ, and Δ so that
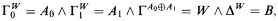
and so as to satisfy all the requirements below.
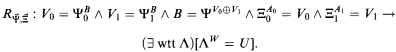
That is, we built a degree-theoretical splitting A0, A1 of W and a set B ≤TW such that if we cannot beat all possible degree-theoretical splittings V0, V1 of B then we were able to witness the fact that U ≤WW (via Λ).
After the proof it was observed that the set U of the proof (page 1222, paragraph 4) needed only to be Δ20. It was then claimed that a consequence to the proof was that every contiguous computably enumerable degree was, in fact, strongly contiguous, in the sense that all (not necessarily computably enumerable) sets of the degree had the same weak truth table degree.