Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-26T16:53:31.844Z Has data issue: false hasContentIssue false
  • English
  • Français

CONSTRUCTIVE REFLECTIVITY PRINCIPLES FOR REGULAR THEORIES

Published online by Cambridge University Press:  30 September 2019

HENRIK FORSSELL  and
PETER LEFANU LUMSDAINE
HENRIK FORSSELL
Affiliation:
DEPARTMENT OF INFORMATICS UNIVERSITY OF OSLO POSTBOKS1080BLINDERN 0316 OSLO, NORWAY and DEPARTMENT OF MATHEMATICS AND SCIENCE EDUCATION UNIVERSITY OF SOUTH-EASTERN NORWAY PAPIRBREDDEN 1 3045 DRAMMEN, NORWAY E-mail: [email protected]
PETER LEFANU LUMSDAINE
Affiliation:
DEPARTMENT OF MATHEMATICS STOCKHOLM UNIVERSITY SE-106 91 STOCKHOLM SWEDENE-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Classically, any structure for a signature ${\rm{\Sigma }}$ may be completed to a model of a desired regular theory ${T}}$ by means of the chase construction or small object argument. Moreover, this exhibits 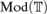${\rm{Mod}}\left(T)$ as weakly reflective in 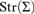${\rm{Str}}\left( {\rm{\Sigma }} \right)$.

We investigate this in the constructive setting. The basic construction is unproblematic; however, it is no longer a weak reflection. Indeed, we show that various reflectivity principles for models of regular theories are equivalent to choice principles in the ambient set theory. However, the embedding of a structure into its chase-completion still satisfies a conservativity property, which suffices for applications such as the completeness of regular logic with respect to Tarski (i.e., set) models.

Unlike most constructive developments of predicate logic, we do not assume that equality between symbols in the signature is decidable. While in this setting, we also give a version of one classical lemma which is trivial over discrete signatures but more interesting here: the abstraction of constants in a proof to variables.

Keywords

03F6503G3018C10regular logicconstructive semanticschoice principles
Type
Articles
Information
The Journal of Symbolic Logic , Volume 84 , Issue 4 , December 2019 , pp. 1348 - 1367
Copyright
Copyright © The Association for Symbolic Logic 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Abiteboul, S., Hull, R., and Vianu, V., Foundations of Databases, Addison-Wesley, Reading, MA, 1995.Google Scholar
Aczel, P., The type theoretic interpretation of constructive set theory, Logic Colloquium ’77 (MacIntyre, A., Pacholski, L., and Paris, J., editors), Studies in Logic and the Foundations of Mathematics, vol. 96, North-Holland, Amsterdam, New York, 1978, pp. 55–66.CrossRefGoogle Scholar
Aczel, P., The relation reflection scheme. Mathematical Logic Quarterly, vol. 54 (2008), no. 1, pp. 5–11.CrossRefGoogle Scholar
Adámek, J., Herrlich, H., Rosický, J., and Tholen, W., On a generalized small-object argument for the injective subcategory problem. Cahiers de Topologie et Géométrie Différentielle Catégoriques, vol. 43 (2002), no. 2, pp. 83–106.Google Scholar
Adámek, J. and Rosický, J., Locally Presentable and Accessible Categories, London Mathematical Society Lecture Note Series, vol. 189, Cambridge University Press, Cambridge, 1994.CrossRefGoogle Scholar
Bell, J. L. and Machover, M., A Course in Mathematical Logic, North-Holland, Amsterdam, New York, Oxford, 1977.Google Scholar
Blass, A., Injectivity, projectivity, and the axiom of choice. Transactions of the American Mathematical Society, vol. 255 (1979), pp. 31–59.CrossRefGoogle Scholar
Coste, M., Lombardi, H., and Roy, M.-F., Dynamical method in algebra: Effective Nullstellensätze, Annals of Pure and Applied Logic, vol. 111 (2001), no. 3, pp. 203–256.CrossRefGoogle Scholar
Diaconescu, R., Institution-independent Model Theory, Studies in Universal Logic, Birkhäuser Verlag, Basel, 2008.Google Scholar
Fitting, M. C., Intuitionistic Logic, Model Theory and Forcing, Studies in Logic and the Foundations of Mathematics, North-Holland, Amsterdam, London, 1969.Google Scholar
Hofmann, M., Extensional concepts in intensional type theory, Ph.D. thesis, University of Edinburgh, 1995.Google Scholar
Johnstone, P. T., Sketches of an Elephant: A Topos Theory Compendium. vol. 1 and 2, Oxford Logic Guides, vol. 43 and 44, The Clarendon Press, Oxford University Press, New York, 2002.Google Scholar
Lambek, J. and Scott, P. J., Introduction to Higher Order Categorical Logic, Cambridge Studies in Advanced Mathematics, vol. 7, Cambridge University Press, Cambridge, 1986.Google Scholar
Rathjen, M., Choice principles in constructive and classical set theories, Logic Colloquium ’02 (Chatzidakis, Z., Koepke, P., and Pohlers, W., editors), Association for Symbolic Logic, Lecture Notes in Logic, vol. 27, Peters, A. K., Wellesley, MA, 2006, pp. 299–326.Google Scholar
Troelstra, A. S. and van Dalen, D., Constructivism in Mathematics, Studies in Logic and the Foundations of Mathematics, vol. 121 and 123, North-Holland, Amsterdam, 1988.Google Scholar
van den Berg, B. and Moerdijk, I., The axiom of multiple choice and models for constructive set theory. Journal of Mathematical Logic, vol. 14 (2014), no. 1, 1450005.CrossRefGoogle Scholar
Veldman, W., An intuitionistic completeness theorem for intuitionistic predicate logic, this Journal, vol. 41 (1976), no. 1, pp. 159–166.Google Scholar