Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Orgass, R.J.
1970.
Some results concerning proofs of statements about programs.
Journal of Computer and System Sciences,
Vol. 4,
Issue. 1,
p.
74.
1974.
Generalized Recursion Theory - Proceedings of the 1972 Oslo Symposium.
Vol. 79,
Issue. ,
p.
446.
Myhill, John
1984.
Paradoxes.
Synthese,
Vol. 60,
Issue. 1,
p.
129.
Myhill, John
1984.
Foundations: Logic, Language, and Mathematics.
p.
129.
Flagg, Robert C.
and
Myhill, John
1987.
Implication and analysis in classical frege structures.
Annals of Pure and Applied Logic,
Vol. 34,
Issue. 1,
p.
33.
1992.
Bibliography.
Annals of Pure and Applied Logic,
Vol. 56,
Issue. 1-3,
p.
3.
Coquand, Thierry
1994.
Types for Proofs and Programs.
Vol. 806,
Issue. ,
p.
62.
Cantini, Andrea
1995.
Levels of Truth.
Notre Dame Journal of Formal Logic,
Vol. 36,
Issue. 2,
Andrea, Cantini
2009.
Logic from Russell to Church.
Vol. 5,
Issue. ,
p.
875.
Updike, Eric Thomas
2012.
Abstraction in Fitch's Basic Logic.
History and Philosophy of Logic,
Vol. 33,
Issue. 3,
p.
215.
Crosilla, Laura
2015.
Evolving Computability.
Vol. 9136,
Issue. ,
p.
13.
Coquand, Thierry
2021.
Paul Lorenzen -- Mathematician and Logician.
Vol. 51,
Issue. ,
p.
47.
Crosilla, Laura
2022.
Objects, Structures, and Logics.
Vol. 339,
Issue. ,
p.
287.



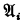 or
or 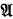 being obtained by juxtaposition from atomic symbols and variables ranging over strings of atomic symbols.
being obtained by juxtaposition from atomic symbols and variables ranging over strings of atomic symbols.