Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Thurber, John J.
1994.
Recursive and r.e. quotient Boolean algebras.
Archive for Mathematical Logic,
Vol. 33,
Issue. 2,
p.
121.
Davey, Kevin J.
1994.
Inseparability in recursive copies.
Annals of Pure and Applied Logic,
Vol. 68,
Issue. 1,
p.
1.
Knight, J.F.
1998.
Handbook of Recursive Mathematics - Volume 1: Recursive Model Theory.
Vol. 138,
Issue. ,
p.
289.
Ash, C.J.
1998.
Handbook of Recursive Mathematics - Volume 1: Recursive Model Theory.
Vol. 138,
Issue. ,
p.
167.
Downey, R.G.
1998.
Handbook of Recursive Mathematics - Volume 2: Recursive Algebra, Analysis and Combinatorics.
Vol. 139,
Issue. ,
p.
823.
Goncharov, Sergey
Harizanov, Valentina
Knight, Julia
McCoy, Charles
Miller, Russell
and
Solomon, Reed
2005.
Enumerations in computable structure theory.
Annals of Pure and Applied Logic,
Vol. 136,
Issue. 3,
p.
219.
MONTALBÁN, ANTONIO
2006.
INDECOMPOSABLE LINEAR ORDERINGS AND HYPERARITHMETIC ANALYSIS.
Journal of Mathematical Logic,
Vol. 06,
Issue. 01,
p.
89.
Montalbán, Antonio
2009.
Mathematical Theory and Computational Practice.
Vol. 5635,
Issue. ,
p.
372.
Alaev, P. E.
Thurber, J.
and
Frolov, A. N.
2009.
Computability on linear orderings enriched with predicates.
Algebra and Logic,
Vol. 48,
Issue. 5,
p.
313.
DOWNEY, ROD
LEMPP, STEFFEN
and
WU, GUOHUA
2010.
ON THE COMPLEXITY OF THE SUCCESSIVITY RELATION IN COMPUTABLE LINEAR ORDERINGS.
Journal of Mathematical Logic,
Vol. 10,
Issue. 01n02,
p.
83.
Kach, Asher
2010.
Depth zero Boolean algebras.
Transactions of the American Mathematical Society,
Vol. 362,
Issue. 8,
p.
4243.
Harrison-Trainor, Matthew
2018.
There is no classification of the decidably presentable structures.
Journal of Mathematical Logic,
Vol. 18,
Issue. 02,
p.
1850010.
Bazhenov, Nikolay
2020.
Computer Science – Theory and Applications.
Vol. 12159,
Issue. ,
p.
142.
Aleksandrova, Svetlana
Bazhenov, Nikolay
and
Zubkov, Maxim
2023.
Complexity of $$\Sigma ^0_n$$-classifications for definable subsets.
Archive for Mathematical Logic,
Vol. 62,
Issue. 1-2,
p.
239.
GONZALEZ, DAVID
and
ROSSEGGER, DINO
2024.
SCOTT SENTENCE COMPLEXITIES OF LINEAR ORDERINGS.
The Journal of Symbolic Logic,
p.
1.
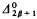 linear ordering of type τ, then there is a recursive ordering of type ωβ · τ.
linear ordering of type τ, then there is a recursive ordering of type ωβ · τ.