Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-22T23:11:14.566Z Has data issue: false hasContentIssue false
  • English
  • Français

Constructible falsity and inexact predicates

Published online by Cambridge University Press:  12 March 2014

Ahmad Almukdad  and
David Nelson
Ahmad Almukdad
Affiliation:
George Washington University, Washington, D.C. 20052
David Nelson
Affiliation:
George Washington University, Washington, D.C. 20052
Get access Rights & Permissions [Opens in a new window]

Extract

In 1949 Nelson [5] proposed a constructive logic in which falsity is conceived in a fashion analogous to that for intuitionistic truth. The predicate calculus N (for strong negation) was characterized by the usual axioms and rules for positive intuitionistic connectives (see Kleene [4, p. 82, la–7 and 9–12]), with the additional axiom schemata for strong negation: A ⊃ (¬A ⊃ B),

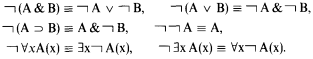
Nelson's paper showed that N may be interpreted with concepts for constructive truth (P-realizability) and falsity (N-realizability). The paper also gave mappings between the intuitionistic and strong negation systems of arithmetic.

These mappings are easily adapted to pure predicate calculus. One shows that intuitionistic predicate calculus I is a subsystem of N by reading the intuitionistic negation of A as A ⊃ B & ¬B in N. It is possible to map N into a subsystem of I using the definition of A′ in [5, p. 19] changing only the definition of (¬A)′ for atomic A to A ⊃ B & ¬B.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 49 , Issue 1 , March 1984 , pp. 231 - 233
Copyright
Copyright © Association for Symbolic Logic 1984

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Cleave, J. P., The notion of logical consequence in the logic of inexact predicates, Zeitschrift für Mathematische Logik unci Grundlagen der Mathematik, vol. 20 (1974), pp. 307–324.CrossRefGoogle Scholar
[2]Hájek, P., Bendove, K. and Renc, Z., The GUHA method and the three-valued logic, Kybernetika, vol. 7 (1971), pp. 421–435.Google Scholar
[3]Körner, S., Experience and theory, Kegan Paul, London, 1966.Google Scholar
[4]Kleene, S. C., Introduction to metamathematics, North-Holland, Amsterdam, 1952.Google Scholar
[5]Nelson, David, Constructible falsity, this Journal, vol. 14 (1949), pp. 16–26.Google Scholar
[6]Thomason, R. H., A semantical study of constructible falsity, Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, vol. 15 (1969), pp. 247–257.CrossRefGoogle Scholar