Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-22T19:20:12.241Z Has data issue: false hasContentIssue false
  • English
  • Français

THE CONSISTENCY STRENGTH OF LONG PROJECTIVE DETERMINACY

Published online by Cambridge University Press:  18 November 2019

JUAN P. AGUILERA  and
SANDRA MÜLLER
JUAN P. AGUILERA
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF GHENT KRIJGSLAAN 281-S8, B9000 GHENT BELGIUM and INSTITUTE OF DISCRETE MATHEMATICS AND GEOMETRY VIENNA UNIVERSITY OF TECHNOLOGY WIEDNER HAUPTSTRAßE 8-10, 1040 VIENNA AUSTRIA E-mail:[email protected]
SANDRA MÜLLER
Affiliation:
INSTITUT FÜR MATHEMATIK, UZA 1 UNIVERSITÄT WIEN AUGASSE 2-6, 1090 WIEN AUSTRIA E-mail:[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We determine the consistency strength of determinacy for projective games of length ω2. Our main theorem is that 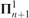$\Pi _{n + 1}^1 $-determinacy for games of length ω2 implies the existence of a model of set theory with ω + n Woodin cardinals. In a first step, we show that this hypothesis implies that there is a countable set of reals A such that Mn (A), the canonical inner model for n Woodin cardinals constructed over A, satisfies 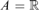$$A = R$$ and the Axiom of Determinacy. Then we argue how to obtain a model with ω + n Woodin cardinal from this.

We also show how the proof can be adapted to investigate the consistency strength of determinacy for games of length ω2 with payoff in 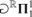$^R R\Pi _1^1 $ or with σ-projective payoff.

Keywords

03E4503E6003E1503E55infinite gamedeterminacyinner model theorylarge cardinallong gamemouse
Type
Articles
Information
The Journal of Symbolic Logic , Volume 85 , Issue 1 , March 2020 , pp. 338 - 366
Copyright
Copyright © The Association for Symbolic Logic 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Aguilera, J. P., σ-Projective determinacy, submitted, 2018.Google Scholar
Aguilera, J. P. and Müller, S., Projective Games on the Reals, 2019. Preprint available at https://muellersandra.github.io/publications/.Google Scholar
Aguilera, J. P., Müller, S., and Schlicht, P., Long games and σ-projective sets, 2018 submitted, . Preprint available at https://muellersandra.github.io/publications/.Google Scholar
Friedman, H. M., Higher set theory and mathematical practice. Annals of Mathematical Logic, vol. 2 (1971), no. 3, pp. 325–357.CrossRefGoogle Scholar
Fuchs, G., Neeman, I., and Schindler, R., A Criterion for coarse iterability. Archive for Mathematical Logic, vol. 49 (2010), pp. 447–467.Google Scholar
Harrington, L. A., Analytic determinacy and 0#, this Journal, vol. 43 (1978), pp. 685–693.Google Scholar
Harrington, L. A. and Kechris, A. S., On the determinacy of games on ordinals. Annals of Mathematical Logic, vol. 20 (1981), pp. 109–154.CrossRefGoogle Scholar
Kanamori, A., The Higher Infinite: Large Cardinals in Set Theory from their Beginnings, Springer Monographs in Mathematics, Springer, 2008.Google Scholar
Kechris, A. S., The Axiom of determinancy implies dependent choices in L (R), this Journal, vol. 49 (1984), no. 1, pp. 161–173.Google Scholar
Kechris, A. S. and Moschovakis, Y. N., Notes on the theory of scales, Games, Scales and Suslin Cardinals, the Cabal Seminar, vol. i (Kechris, A. S., Löwe, B., and Steel, J. R., editors), Cambridge University Press, New York, 2008, pp. 28–74.CrossRefGoogle Scholar
Kechris, A. and Solovay, R., On the relative consistency strength of determinacy hypotheses. Transactions of the American Mathematical Society, vol. 290 (1985), no. 1, pp. 179–211.Google Scholar
Martin, D. A., Measurable cardinals and analytic games. Fundamenta Mathematicae, vol. 66 (1970), pp. 287–291.Google Scholar
Martin, D. A., Borel determinacy. Annals of Mathematics, vol. 102 (1975), no. 2, pp. 363–371.CrossRefGoogle Scholar
Martin, D. A. and Steel, J. R., A proof of projective determinacy. Journal of the American Mathematical Society, vol. 2 (1989), pp. 71–125.CrossRefGoogle Scholar
Martin, D. A. and Steel, J. R., Iteration trees. Journal of the American Mathematical Society, vol. 7 (1994), no. 1, pp. 1–73.Google Scholar
Martin, D. A. and Steel, J. R., The extent of scales in $L\left( R\right)$, Games, Scales, and Suslin Cardinals, the Cabal Seminar, vol. i (Kechris, A. S., Löwe, B., and Steel, J. R., editors), Cambridge University Press, New York, 2008, pp. 110–120.Google Scholar
Mitchell, W. J. and Steel, J. R., Fine Structure and Iteration Trees, Lecture Notes in Logic, Springer-Verlag, Berlin, New York, 1994.Google Scholar
Moschovakis, Y. N., Descriptive Set Theory, second ed., Mathematical Surveys and Monographs, vol. 155, AMS, Providence, RI, 2009.Google Scholar
Müller, S., The axiom of determinacy implies dependent choice in mice. Mathematical Logic Quarterly, vol. 65 (2019), no. 3, pp. 370–375.CrossRefGoogle Scholar
Müller, S. and Sargsyan, G., HOD in inner models with Woodin cardinals, 2018 submitted, . Preprint available at https://muellersandra.github.io/publications/.Google Scholar
Müller, S., Schindler, R., and Woodin, W. H., Mice with finitely many Woodin cardinals from optimal determinacy hypotheses, Journal of Mathematical Logic, 2019. https://doi.org/10.1142/S0219061319500132.CrossRefGoogle Scholar
Neeman, I., Optimal proofs of determinacy. The Bulletin of Symbolic Logic, vol. 1 (1995), no. 3, pp. 327–339.CrossRefGoogle Scholar
Neeman, I., The Determinacy of Long Games, De Gruyter Series in Logic and its Applications, Walter de Gruyter, Berlin, 2004.Google Scholar
Neeman, I.,, Determinacy in $L\left( R\right)$, Handbook of Set Theory (Foreman, M. and Kanamori, A., editors), Springer, Dordrecht, 2010, pp. 1877–1950.CrossRefGoogle Scholar
Sargsyan, G., On the prewellorderings associated with directed systems of mice, this Journal, vol. 78 (2013), no. 3, pp. 735–763.Google Scholar
Sargsyan, G. and Steel, J., The mouse set conjecture for sets of reals, this Journal, vol. 80 (2015), no. 2, p. 671–683.Google Scholar
Schindler, R. and Steel, J. R., The self-iterability of L [E], this Journal, vol. 74 (2009), no. 3, pp. 751–779.Google Scholar
Schindler, R., Steel, J. R., and Zeman, M., Deconstructing inner model theory, this Journal, vol. 67 (2002), pp. 721–736.Google Scholar
Schlutzenberg, F. and Trang, N. D., Scales in hybrid mice over $R$, submitted, 2016.Google Scholar
Steel, J. R., Projectively well-ordered inner models. Annals of Pure and Applied Logic, vol. 74 (1995), pp. 77–104.Google Scholar
Steel, J. R., An optimal consistency strength lower bound for $AD_ R$, unpublished, 2008.Google Scholar
Steel, J. R., Derived models associated to mice, Computational Prospects of Infinity - Part i (Chong, C.-T., editor), Lecture Notes Series, vol. 14, World Scientific, Singapore, 2008, pp. 105–193.Google Scholar
Steel, J. R., Scales in $K\left( R\right)$, Games, Scales and Suslin Cardinals, the Cabal Seminar, vol. I (Kechris, A. S., Löwe, B., and Steel, J. R., editors), Cambridge University Press, New York, 2008, pp. 176–208.CrossRefGoogle Scholar
Steel, J. R., Scales in $L\left( R\right)$, Games, Scales and Suslin Cardinals, the Cabal Seminar, vol. I (Kechris, A. S., Löwe, B., and Steel, J. R., editors), Cambridge University Press, New York, 2008, pp. 130–175.CrossRefGoogle Scholar
Steel, J. R., An outline of inner model theory, Handbook of Set Theory (Foreman, M. and Kanamori, A., editors), Springer, Dordrecht, 2010, pp. 1595–1684.Google Scholar
Steel, J. R., A theorem of Woodin on mouse sets, Ordinal Definability and Recursion Theory, the Cabal Seminar, vol. III (Kechris, A. S., Löwe, B., and Steel, J. R., editors), Cambridge University Press, Cambridge, 2016, pp. 243–256.CrossRefGoogle Scholar
Steel, J. R. and Woodin, W. H., HOD as a core model, Ordinal Definability and Recursion Theory, the Cabal Seminar, vol. III (Kechris, A. S., Löwe, B., and Steel, J. R., editors), Cambridge University Press, Cambridge, 2016, pp. 257–345.CrossRefGoogle Scholar
Trang, N. D., Generalized Solovay measures, the HOD analysis, and the core model induction, Ph.D. thesis, University of California at Berkeley, 2013.Google Scholar
Trang, N. D., Determinacy in $L\left(R {,\mu } \right)$. Journal of Mathematical Logic, vol. 14 (2014), no. 1, 1450006.CrossRefGoogle Scholar
Trang, N. D., Structure theory of $L\left(R {,\mu } \right)$ and its applications, this Journal, vol. 80 (2015), no. 1, pp. 29–55.Google Scholar
Uhlenbrock, S., now Müller, Pure and hybrid mice with finitely many Woodin cardinals from levels of determinacy, Ph.D. thesis, WWU Münster, 2016.Google Scholar
Woodin, W.H., The Axiom of Determinacy, Forcing Axioms, and the Nonstationary Ideal, De Gruyter Series in Logic and its Applications, De Gruyter, Berlin, 2010.CrossRefGoogle Scholar