Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-25T23:05:08.613Z Has data issue: false hasContentIssue false
  • English
  • Français

CONSISTENCY PROOF OF A FRAGMENT OF PV WITH SUBSTITUTION IN BOUNDED ARITHMETIC

Published online by Cambridge University Press:  23 October 2018

YORIYUKI YAMAGATA
YORIYUKI YAMAGATA*
Affiliation:
NATIONAL INSTITUTE OF ADVANCED SCIENCE AND TECHNOLOGY (AIST) INFORMATION TECHNOLOGY RESEARCH INSTITUTE 1-8-31 MIDORIGAOKA, IKEDA, OSAKA 563-8577, JAPANE-mail: [email protected]: https://staff.aist.go.jp/yoriyuki.yamagata/en/
Get access Rights & Permissions [Opens in a new window]

Abstract

This article presents a proof that Buss’s 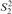$S_2^2$ can prove the consistency of a fragment of Cook and Urquhart’s PV from which induction has been removed but substitution has been retained. This result improves Beckmann’s result, which proves the consistency of such a system without substitution in bounded arithmetic 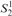$S_2^1$.

Our proof relies on the notion of “computation” of the terms of PV. In our work, we first prove that, in the system under consideration, if an equation is proved and either its left- or right-hand side is computed, then there is a corresponding computation for its right- or left-hand side, respectively. By carefully computing the bound of the size of the computation, the proof of this theorem inside a bounded arithmetic is obtained, from which the consistency of the system is readily proven.

This result apparently implies the separation of bounded arithmetic because Buss and Ignjatović stated that it is not possible to prove the consistency of a fragment of PV without induction but with substitution in Buss’s 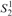$S_2^1$. However, their proof actually shows that it is not possible to prove the consistency of the system, which is obtained by the addition of propositional logic and other axioms to a system such as ours. On the other hand, the system that we have considered is strictly equational, which is a property on which our proof relies.

Keywords

03F3003D15bounded arithmeticconsistency proofcomputational complexity
Type
Articles
Information
The Journal of Symbolic Logic , Volume 83 , Issue 3 , September 2018 , pp. 1063 - 1090
Copyright
Copyright © The Association for Symbolic Logic 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Beckmann, A., Proving consistency of equational theories in bounded arithmetic, this JOURNAL, vol. 67 (2002), no. 1, pp. 279–296.Google Scholar
Beckmann, A., Personal communication, 2015.Google Scholar
Buss, S. R., Bounded Arithmetic, Bibliopolis, Naples, 1986.Google Scholar
Buss, S. R. and Ignjatović, A., Unprovability of consistency statements in fragments of bounded arithmetic. Annals of Pure and Applied Logic, vol. 74 (1995), pp. 221–244.CrossRefGoogle Scholar
Cook, S. A., Feasibly constructive proofs and the propositional calculus (preliminary version), Proceedings of Seventh Annual ACM Symposium on Theory of Computing, Association for Computing Machinery, New York, 1975, pp. 83–97.CrossRefGoogle Scholar
Cook, S. and Urquhart, A., Functional interpretations of feasibly constructive arithmetic. Annals of Pure and Applied Logic, vol. 63 (1993), no. 2, pp. 103–200.CrossRefGoogle Scholar
Kahn, G., Natural semantics, Annual Symposium on Theoretical Aspects of Computer Science (Brandenburg, F. J., Vidal-Naquet, G., and Wirsing, M., editors), Springer-Verlag, Berlin, 1987, pp. 22–39.Google Scholar
Plotkin, G. D., A structural approach to operational semantics, Technical report, Computer Science Department, Aarhus University, Denmark, 1981.Google Scholar
Pudlák, P., A note on bounded arithmetic. Fundamenta Mathematicae, vol. 136 (1990), pp. 85–89.CrossRefGoogle Scholar
Takeuti, G., Some relations among systems for bounded arithmetic, Mathematical Logic (Petkov, P. P., editor), Springer, Boston, MA, 1990, pp. 139–154.CrossRefGoogle Scholar
Wilkie, A. and Paris, J., On the scheme of induction for bounded arithmetic formulas. Annals of Pure and Applied Logic, vol. 35 (1987), pp. 261–302.CrossRefGoogle Scholar
Yamagata, Y., Consistency proof of a feasible arithmetic inside a bounded arithmetic, preprint, 2014, arXiv:1411.7087v2.Google Scholar