Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-22T20:31:17.218Z Has data issue: false hasContentIssue false
  • English
  • Français

The consistency of a system of combinatory restricted generality*

Published online by Cambridge University Press:  12 March 2014

Haskell B. Curry
Haskell B. Curry*
Affiliation:
Pennsylvania State University, University Park, Pennsylvania 16802
Get access Rights & Permissions [Opens in a new window]

Extract

The system 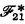, proposed without a claim as to its consistency in [CLg, §15C], has turned out to entail a consequence which is extremely suspicious. For from the axiom ⊦LH it follows that

holds for arbitrary X; hence for X ≡ YH, where Y is a fixed-point combinator, we have

Whether or not this leads to an actual contradiction it would be interesting to know; but, no matter whether it does or not, (2) seems highly counterintuitive.

The aim of this note is to point out that a related system, here called 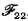, is demonstrably consistent and sufficient for all practical purposes served by 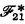, and at the same time to correct an error in [CLg, §15D2], which was discovered too late to be corrected on the proofs. This 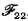is formed from 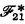by dropping H from the list of θ's, and hence deleting ⊦LH and (1). The new system does not allow inferential rules to be converted into formulas with the same ease as does 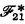; but if one is content with stating the results as rules, 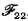is adequate for all the main results deduced for 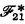in [CLg, §15C–D].

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 38 , Issue 3 , September 1973 , pp. 489 - 492
Copyright
Copyright © Association for Symbolic Logic 1973

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

*

This paper was prepared when the author was Visiting Mellon Professor at the University of Pittsburgh.

References

BIBLIOGRAPHY

[STB]Bunder, Martin V., Set theory based on combinatory logic, Thesis, University of Amsterdam, 1969.Google Scholar
[CLg]Curry, Haskell B., et al., Combinatory logic. Vol. I (with Feys, Robert), North-Holland, Amsterdam, 1959; Vol. II (with J. Roger Hindley and Jonathan P. Seldin), North-Holland, Amsterdam, 1972.Google Scholar
[SIC]Seldin, Jonathan P., Studies in illative combinatory logic, Thesis, University of Amsterdam, 1968.Google Scholar