Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-25T00:31:17.684Z Has data issue: false hasContentIssue false
  • English
  • Français

Consistency notions in illative combinatory logic

Published online by Cambridge University Press:  12 March 2014

M. W. Bunder
M. W. Bunder*
Affiliation:
Wollongono University, Wollongong N.S.W. 2500, Australia
Get access Rights & Permissions [Opens in a new window]

Extract

In this paper we show that certain notions of consistency currently in use in illative combinatory logic are not always necessary nor always sufficient for the acceptability of the system.

The three notions of consistency we will consider are:

(A) Not all terms of the system are assertible.

(B) Not all propositions of the system are assertible.

(C) The system is Q-consistent, i.e. if Q (for equality) is in or is added to the system as a primitive with axioms such as

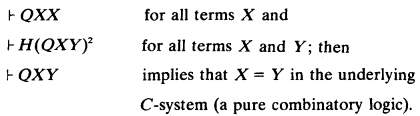
Post defined a system of propositional calculus to be inconsistent if all propositions were assertible. In a more general system where there may be terms which are not propositions (although all propositions are terms), we need to distinguish notions (A) and (B) as two possible consistency notions “in the sense of Post”.

In [3] Curry and Feys assume that Q is in the system defined as λxλy.Ξ(C*x)(C*y) or as a primitive, but Seldin in [5] also talks about Q-consistency of a system (F22) to which Q has to be added. We therefore consider the definition of Q-consistency that includes all three possibilities.

In [3] Curry and Feys state that Q-consistency is essential for acceptability. This is because there the purpose was to have an assertional system of illative combinatory logic in which combinatory equality was represented by the assertion of QXY. However if Q is to represent some other form of equality, Q-consistency may become inessential for acceptability or even incompatible with it.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 42 , Issue 4 , December 1977 , pp. 527 - 529
Copyright
Copyright © Association for Symbolic Logic 1977

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Bunder, M. W. and Seldin, J. P., Some anomalies in Fitch's system OD (to appear).Google Scholar
[2]Curry, H. B., The consistency of a system of combinatory restricted generality, this Journal, vol. 38 (1973), pp. 489–492.Google Scholar
[3]Curry, H. B. and Feys, R., Combinatory logic, vol. 1, North-Holland, Amsterdam, 1959.Google Scholar
[4]Fitch, F. B., Elements of combinatory logic, Yale University Press, New Haven, 1974.Google Scholar
[5]Seldin, J. P., The Q-consistency of ℱ22, The Notre Dame Journal of Formal Logic, vol. 18 (1977), pp. 117–127.Google Scholar