Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-22T20:05:21.521Z Has data issue: false hasContentIssue false
  • English
  • Français

Conservative extensions of models of set theory and generalizations

Published online by Cambridge University Press:  12 March 2014

Ali Enayat
Ali Enayat*
Affiliation:
Department of Mathematics, Western Illinois University, Macomb, Illinois 61455
*
Department of Mathematics and Computer Science, San Jose State University, 1, Washington Square, San Jose, California 95192-0103.
Get access Rights & Permissions [Opens in a new window]

Extract

An attempt to answer the following question gave rise to the results of the present paper. Let 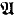be an arbitrary model of set theory. Does there exist an elementary extension 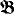of 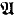satisfying the two requirements: (1) 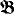contains an ordinal exceeding all the ordinals of 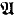; (2) 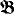does not enlarge any (hyper) integer of 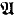? Note that a trivial application of the ordinary compactness theorem produces a model satisfying condition (1); and an internal ultrapower modulo an internal ultrafilter produces a model satisfying condition (2) (but not (1), because of the axiom of replacement). Also, such a 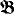satisfying both conditions (1) and (2) exists if the external cofinality of the ordinals of 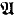is countable, since by [KM], 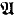would then have an elementary end extension.

Using a class of models constructed by M. Rubin using 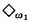in [RS], and already employed in [E1], we prove that our question in general has a negative answer (see Theorem 2.3). This result generalizes the results of M. Kaufmann and the author (appearing respectively in [Ka] and [E1]) concerning models of set theory with no elementary end extensions.

In the course of the proof it was necessary to establish that all conservative extensions (see Definition 2.1) of models of ZF must be cofinal. This is in direct contrast with the case of Peano arithmetic where all conservative extensions are end extensional (as observed by Phillips in [Ph1]). This led the author to introduce two useful weakenings of the notion of a conservative end extension which, as shown by the “completeness” theorems in §3, can exist.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 51 , Issue 4 , December 1986 , pp. 1005 - 1021
Copyright
Copyright © Association for Symbolic Logic 1986

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[Ba]Baumgartner, J., Ineffability properties of cardinals. I, Infinite and finite sets (Hajnal, A.et al., editors), Vol. I, North-Holland, Amsterdam, 1975, pp. 109–130.Google Scholar
[BJ]Boolos, G. and Jeffrey, R. C., Computability and logic, Cambridge University Press, Cambridge, 1974.Google Scholar
[B1]Blass, A., On certain types and models for arithmetic, this Journal, vol. 39 (1974), pp. 151–162.Google Scholar
[B2]Blass, A., A model without ultrafilters, Bulletin de l'Académie Polonaise des Sciences, Série des Sciences Mathématiques, Astronomiques et Physiques, vol. 25 (1977), pp. 329–331.Google Scholar
[E1]Enayat, A., On certain elementary extensions of models of set theory, Transactions of the American Mathematical Society, vol. 283 (1984), pp. 705–715.CrossRefGoogle Scholar
[E2]Enayat, A., Weakly compact cardinals in models of set theory, this Journal, vol. 50 (1985), pp. 476–486.Google Scholar
[Ff]Feferman, S., Some applications of the notion of forcing and generic sets, Fundamenta Mathematicae, vol. 56 (1965), pp. 324–345.Google Scholar
[Fg]Felgner, U., Comparison of the axioms of local and universal choice, Fundamenta Mathematicae, vol. 71 (1971), pp. 43–62.CrossRefGoogle Scholar
[Ka]Kaufmann, M., Blunt and topless end extensions of models of set theory, this Journal, vol. 48 (1983), pp. 1053–1073.Google Scholar
[K1]Keisler, H. J., Logic with the quantifier “there exist uncountably many”, Annals of Mathematical Logic, vol. 1 (1970), pp. 1–94.CrossRefGoogle Scholar
[K2]Keisler, H. J., Model theory for infinitary logic, North-Holland, Amsterdam, 1971.Google Scholar
[K3]Keisler, H. J., Models with tree structures, Proceedings of the Tarski symposium (Henkin, L.et al., editors), Proceedings of Symposia in Pure Mathematics, vol. 25, American Mathematical Society, Providence, Rhode Island, 1974, pp. 331–348.CrossRefGoogle Scholar
[KM]Keisler, H.J. and Morley, M., Elementary extensions of models of set theory, Israel Journal of Mathematics, vol. 5 (1968), pp. 49–65.CrossRefGoogle Scholar
[Ko]Kotlarski, H., On cofinal extensions of models of arithmetic, this Journal, vol. 48 (1983), pp. 311–320.Google Scholar
[O]Odifreddi, P., Forcing and reducibilities, this Journal, vol. 48 (1983), pp. 288–310.Google Scholar
[P]Paris, J. B., Minimal models of ZF, Proceedings of the Bertrand Russell memorial logic conference (Uldum, Denmark, 1971; Bell, J.et al., editors), Bertrand Russell Memorial Logic Conference, Leeds, 1973, pp. 327–331.Google Scholar
[Ph1]Phillips, R. G., Omitting types in arithmetic and conservative extensions, Victoria symposium on nonstandard analysis (Hurd, A. and Loeb, P., editors), Lecture Notes in Mathematics, vol. 369, Springer-Verlag, Berlin and New York, 1974, pp. 195–202.CrossRefGoogle Scholar
[Ph2]Phillips, R. G., A minimal extension that is not conservative, Michigan Mathematical Journal, vol. 21 (1974), pp. 27–32.CrossRefGoogle Scholar
[Po]Potthoff, K., A simple tree lemma and its application to a counterexample of Phillips, Archiv für Mathematische Logik und Grundlagenforschung, vol. 18 (1976), pp. 67–71.CrossRefGoogle Scholar
[RS]Rubin, M. and Shelah, S., On the elementary equivalence of automorphism groups of Boolean algebras; downward Skolem Löwenheim theorems and compactness of related quantifiers, this Journal, vol. 45 (1980), pp. 265–283.Google Scholar
[Seh1]Schmerl, J., On κ-like structures which embed closed unbounded sets, Annals of Mathematical Logic, vol. 10 (1976), pp. 289–314.CrossRefGoogle Scholar
[Sch2]Schmerl, J., Recursively saturated rather classless models of Peano arithmetic, Logic year 1979–80 (Storrs, Connecticut; Lerman, M.et al., editors), Lecture Notes in Mathematics, vol. 859, Springer-Verlag, Berlin and New York, 1981, pp. 268–282.CrossRefGoogle Scholar
[SS]Schmerl, J. and Shelah, S., On power-like models for hyperinaccessible cardinals, this Journal, vol. 37 (1972), pp. 531–537.Google Scholar
[Sh]Shelah, S., Models with second-order properties. II: Trees with no undefined branches, Annals of Mathematical Logic, vol. 14 (1978), pp. 73–87.CrossRefGoogle Scholar