Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-16T17:12:41.674Z Has data issue: false hasContentIssue false
  • English
  • Français

CONSEQUENCES OF THE EXISTENCE OF AMPLE GENERICS AND AUTOMORPHISM GROUPS OF HOMOGENEOUS METRIC STRUCTURES

Published online by Cambridge University Press:  14 September 2016

MACIEJ MALICKI
MACIEJ MALICKI*
Affiliation:
DEPARTMENT OF MATHEMATICS AND MATHEMATICAL ECONOMICS WARSAW SCHOOL OF ECONOMICS AL. NIEPODLEGLOSCI 162 02-554, WARSAW, POLANDE-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We define a simple criterion for a homogeneous, complete metric structure X that implies that the automorphism group Aut(X) satisfies all the main consequences of the existence of ample generics: it has the automatic continuity property, the small index property, and uncountable cofinality for nonopen subgroups. Then we verify it for the Urysohn space 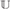$$, the Lebesgue probability measure algebra MALG, and the Hilbert space 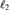$\ell _2 $, thus proving that Iso(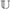$$), Aut(MALG), 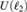$U\left( {\ell _2 } \right)$, and 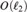$O\left( {\ell _2 } \right)$ share these properties. We also formulate a condition for X which implies that every homomorphism of Aut(X) into a separable group K with a left-invariant, complete metric, is trivial, and we verify it for 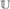$$, and 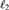$\ell _2 $.

Keywords

03E1554H1137B05metric structuresautomatic continuitysmall index propertyuncountable cofinalityPolish groups
Type
Articles
Information
The Journal of Symbolic Logic , Volume 81 , Issue 3 , September 2016 , pp. 876 - 886
Copyright
Copyright © The Association for Symbolic Logic 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Becker, H. and Kechris, A., The Descriptive Set Theory of Polish Group Actions, Cambridge University Press, Cambridge, 1996.CrossRefGoogle Scholar
Ben Yaacov, I., Berenstein, A., and Melleray, J., Polish topometric groups . Transactions of the American Mathematical Society, vol. 365 (2013), pp. 3877–3897.CrossRefGoogle Scholar
Ben Yaacov, I., Berenstein, A., Henson, W., and Usvyatsov, A., Model theory for metric structures , Model Theory with Applications to Algebra and Analysis, vol. 2, London Mathematical Society Lecture Note Series, vol. 350, Cambridge University Press, Cambridge, 2008, pp. 315–427.Google Scholar
Bryant, R.M. and Evans, D. M., The small index property for free groups and relatively free groups . Journal of the London Mathematical Society, vol. 55 (1997), pp. 363–369.CrossRefGoogle Scholar
del Junco, A., Disjointness of Measure-Preserving Transformations, Minimal Self-Joinings and Category , Ergodic Theory and Dynamical Systems, I (College Park, Maryland, 1979–80), Progress in Mathematics, vol. 10, Birkhäuser, Boston, Massachusetts, 1981, pp. 81–89.Google Scholar
Gao, S., Invariant Descriptive Set Theory, Chapman and Hall, 2008.CrossRefGoogle Scholar
Glasner, E. and Weiss, B., Topological groups with Rokhlin properties . Colloquium Mathematicum, vol. 110 (2008), pp. 51–80.CrossRefGoogle Scholar
Hodges, W., Hodkinson, I., Lascar, D., and Shelah, D., The small index property for ω-stable ω-categorical structures and for the random graph . Journal of the London Mathematical Society, vol. 48 (1993), pp. 204–218.CrossRefGoogle Scholar
Hrushovski, E., Extending partial isomorphisms of graphs . Combinatorica, vol. 12 (1992), pp. 411–416.CrossRefGoogle Scholar
Katětov, M., On universal metric spaces , General Topology and its Relations to Modern Analysis and Algebra VI (Frolík, Z., editor), Proceedings of Sixth Prague Topological Symposium 1986, Heldermann Verlag, 1988, pp. 323–330.Google Scholar
Kaïchouh, A. and Le Maître, F., Connected Polish groups with ample generics, arXiv:1503.04298.Google Scholar
Kechris, A. and Rosendal, C., Turbulence, amalgamation, and generic automorphisms of homogeneous structures . Proceedings of the London Mathematical Society (3), vol. 94 (2007), no. 2, pp. 302–350.CrossRefGoogle Scholar
Malicki, M., The automorphism group of the Lebesgue measure has no non-trivial subgroups of index < 2 ω . Colloquium Mathematicum, vol. 133 (2013), pp. 169–174.CrossRefGoogle Scholar
Malicki, M., Generic elements in isometry groups of Polish ultrametric spaces . Israel Journal of Mathematics, vol. 206 (2015), pp. 127–153.CrossRefGoogle Scholar
Malicki, M., An example of a non non-archimedean Polish group with ample generics. Proceedings of the American Mathematical Society , to appear.Google Scholar
Ricard, E. and Rosendal, C., On the algebraic structure of the unitary group . Collectanea Mathematica, vol. 58 (2007), pp. 181–192.Google Scholar
Rosendal, C., A topological version of the Bergman property . Forum Mathematicum, vol. 21 (2009), pp. 299–332.CrossRefGoogle Scholar
Rosendal, C. and Solecki, S., Automatic continuity of homomorphisms and fixed points on metric compacta . Israel Journal of Mathematics, vol. 162 (2007), pp. 349–371.CrossRefGoogle Scholar
Sabok, M., Automatic continuity for isometry groups, preprint, arXiv:1312.5141v2.Google Scholar
Schmerl, J.H., Generic automorphisms and graph coloring . Discrete Mathematics, vol. 291 (2005), pp. 235–242.CrossRefGoogle Scholar
Solecki, S., Extending partial isometries . Israel Journal of Mathematics, vol. 150 (2005), pp. 315–331.CrossRefGoogle Scholar
Tsankov, T., Automatic continuity for the unitary group . Proceedings of the American Mathematical Society, vol. 141 (2013), pp. 3673–3680.CrossRefGoogle Scholar