In the paper [S1] I introduced a game, denoted by MG(J) (where J is a free ideal on some infinite set S) and called “the meager nowhere dense game for J”. The special case when J is the collection of finite subsets of the set S is called the countable-finite game on S. It proceeds as follows.

First player ONE picks a countable set C 1, then player TWO picks a finite set F 1. Then in the second inning ONE picks a countable set C 2 with C 1 ⊂ C 2 (unless explicitly indicated otherwise, “⊂” means “is a proper subset of”) and TWO responds with a finite set F 2, and so on. The players construct a sequence (C1,F1,C2,F2,…,Ck,Fk,…) where for each positive integer k

(i) Ck denotes ONE's countable set picked during the kth inning,

(ii) Fk denotes TWO's finite set picked during the kth inning, and

(iii) Ck ⊂ Ck + 1.

Such a sequence is a play of the countable-finite game on S, and TWO wins this play if 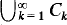is contained in 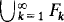. The notion of a winning perfect information strategy is defined as usual (see, for example, [S1]). Zermelo-Fraenkel set theory together with the axiom of choice (denoted by ZFC; for a statement of the axioms see pp. xv–xvi of [K]) is a strong enough theory to build a winning perfect information strategy for player TWO in this game.

Does TWO have a winning strategy requiring less than perfect information? Fix a positive integer k. A strategy of TWO which requires knowledge of only at the most the k most recent moves of ONE is said to be a k-tactic. For the countable-finite game on an infinite set S the following facts about the existence of winning k-tactics for TWO are proved in [S1]:

1) TWO does not have a winning 1-tactic (Theorem 1 of [S1]).

2) If the cardinality of S is less than ℵ2 then TWO has a winning 2-tactic (Corollary 4 of [S1]).

3) If TWO has a winning k-tactic in the countable-finite game on an infinite set S, then TWO has a winning 3-tactic (Proposition 15 of [SI]).